Decoding the Universe with AI

A Decade of Progress and the Road Ahead

FAIR Universe Challenge, NeurIPS 2025, San Diego

François Lanusse










slides at eiffl.github.io/talks/SanDiego2025

What are cosmologists trying to go after with galaxy surveys?


















Image credit: N. Jeffrey / DES Collaboration
Image credit: Euclid Consortium / Planck Collaboration / A. Mellinger



















Stage II: SDSS

Image credit: Peter Melchior



















Stage III: DES

Image credit: Peter Melchior



















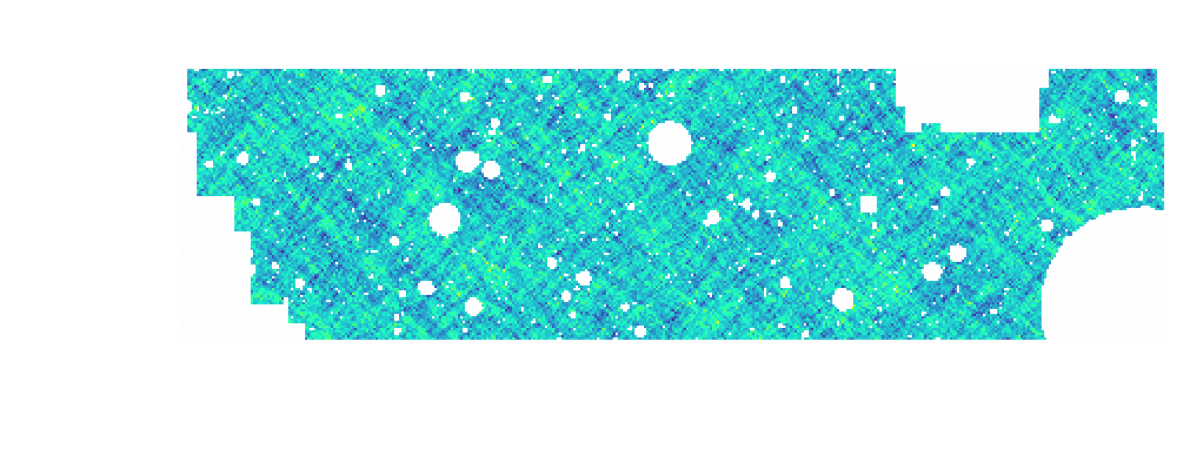
Stage IV: Rubin Observatory LSST (HSC)

Image credit: Peter Melchior

the Vera C. Rubin Observatory Legacy Survey of Space and Time



  • 1000 images each night, 15 TB/night for 10 years

  • 18,000 square degrees, observed once every few days

  • Tens of billions of objects, each one observed $\sim1000$ times










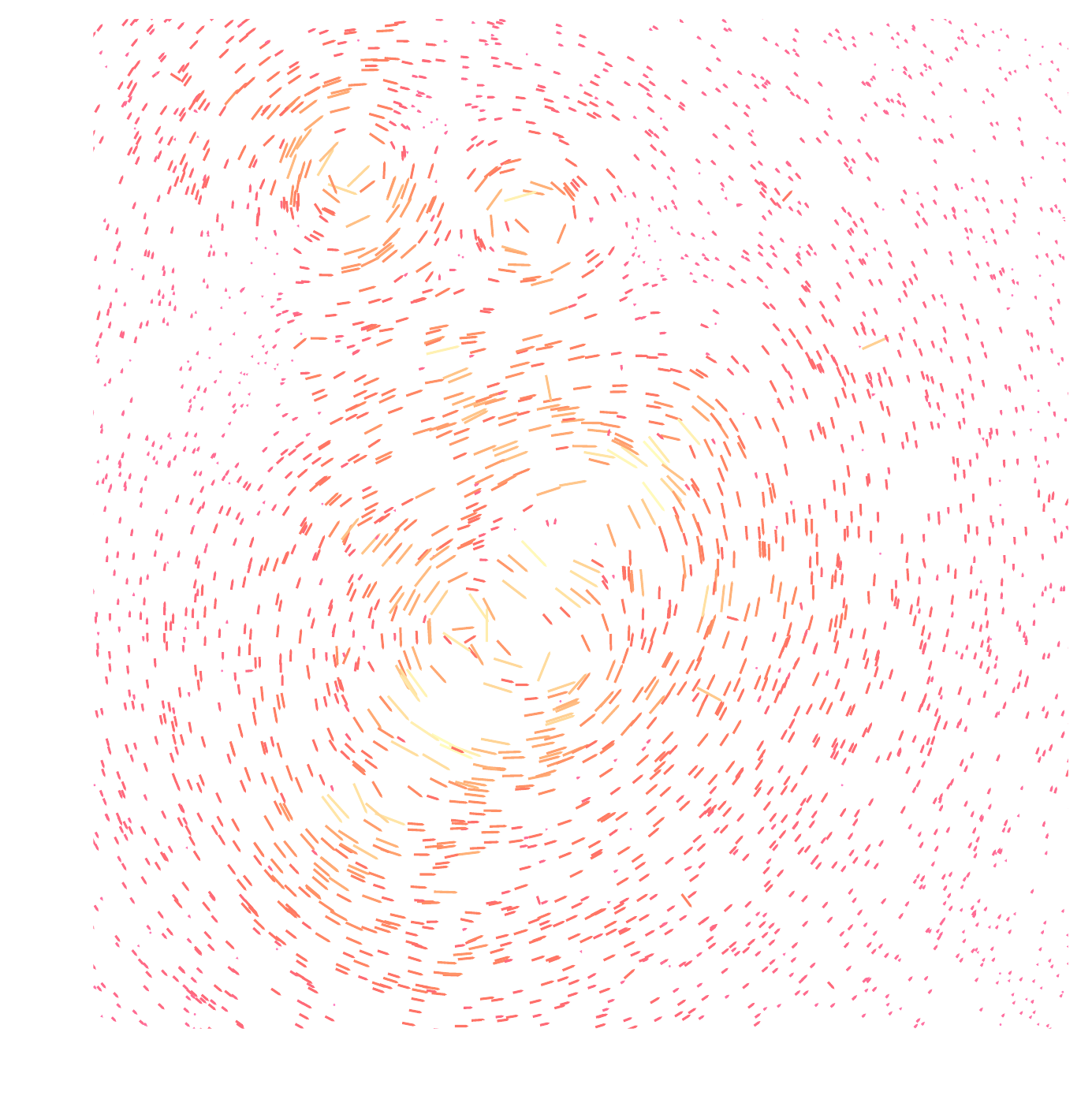
Let's set the stage: Gravitational lensing

Galaxy shapes as estimators for gravitational shear
$$ e = \gamma + e_i \qquad \mbox{ with } \qquad e_i \sim \mathcal{N}(0, I)$$
  • We are trying the measure the ellipticity $e$ of galaxies as an estimator for the gravitational shear $\gamma$

From Gravitational Shear to Convergence

Shear $\gamma$
Convergence $\kappa$
$$\gamma_1 = \frac{1}{2} (\partial_1^2 - \partial_2^2) \ \Psi \quad;\quad \gamma_2 = \partial_1 \partial_2 \ \Psi \quad;\quad \kappa = \frac{1}{2} (\partial_1^2 + \partial_2^2) \ \Psi$$
$$\boxed{\gamma = \mathbf{P} \kappa}$$

The limits of traditional cosmological inference

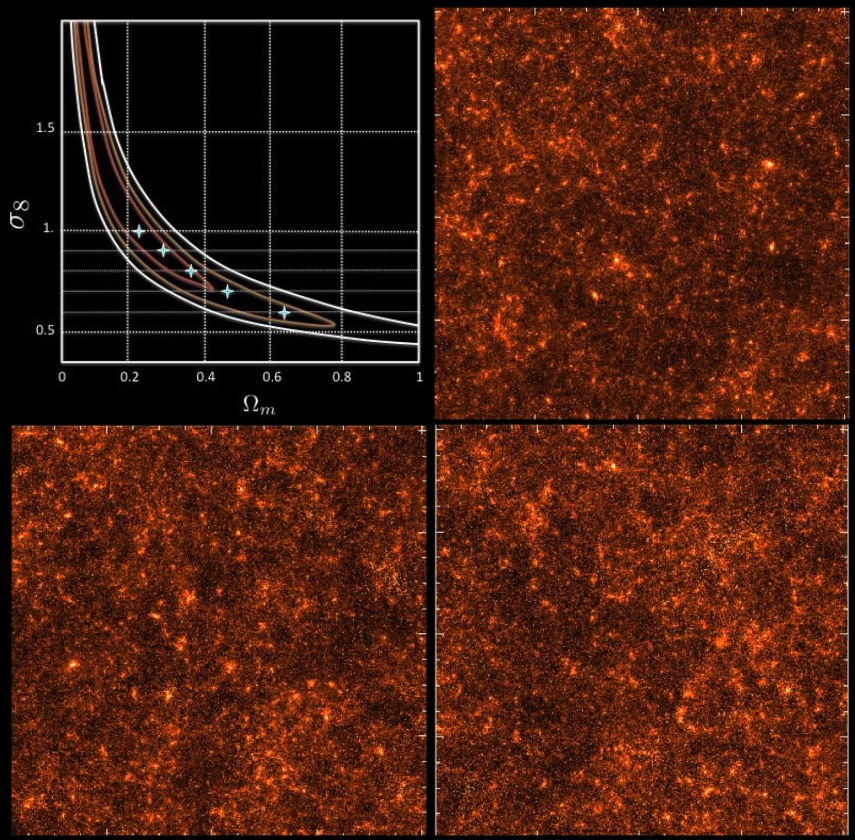
HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
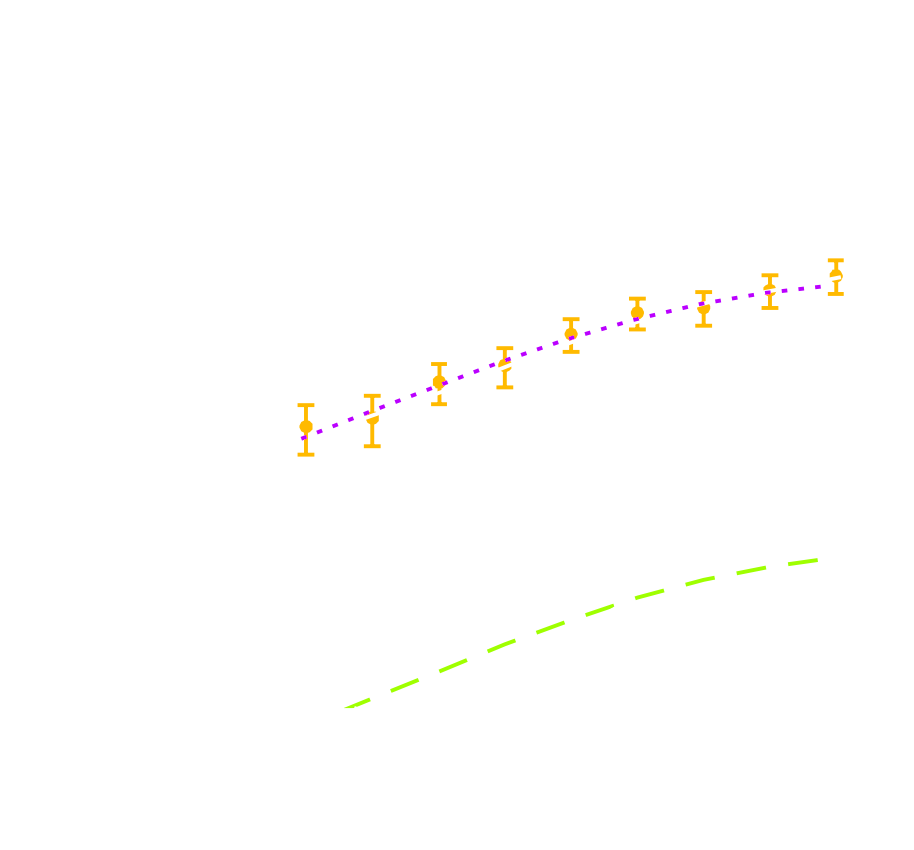
(Hikage et al. 2018)
  • Measure the ellipticity $\epsilon = \epsilon_i + \gamma$ of all galaxies
    $\Longrightarrow$ Noisy tracer of the weak lensing shear $\gamma$

  • Compute summary statistics based on 2pt functions,
    e.g. the power spectrum

  • Run an MCMC to recover a posterior on model parameters, using an analytic likelihood $$ p(\theta | x ) \propto \underbrace{p(x | \theta)}_{\mathrm{likelihood}} \ \underbrace{p(\theta)}_{\mathrm{prior}}$$
Main limitation: the need for an explicit likelihood
We can only compute from theory the likelihood for simple summary statistics and on large scales

$\Longrightarrow$ We are dismissing a significant fraction of the information!

The search for optimal summary statistics

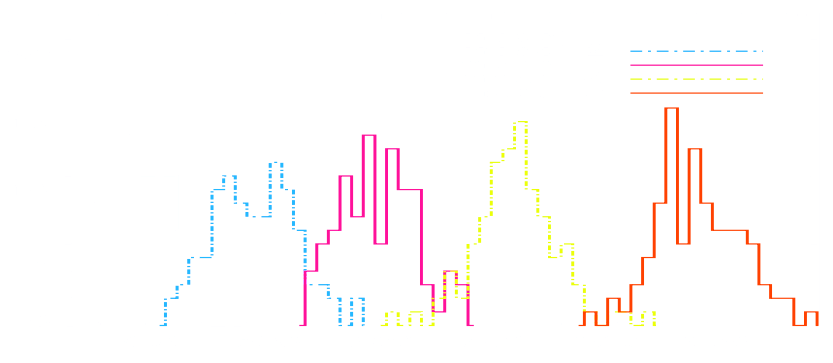
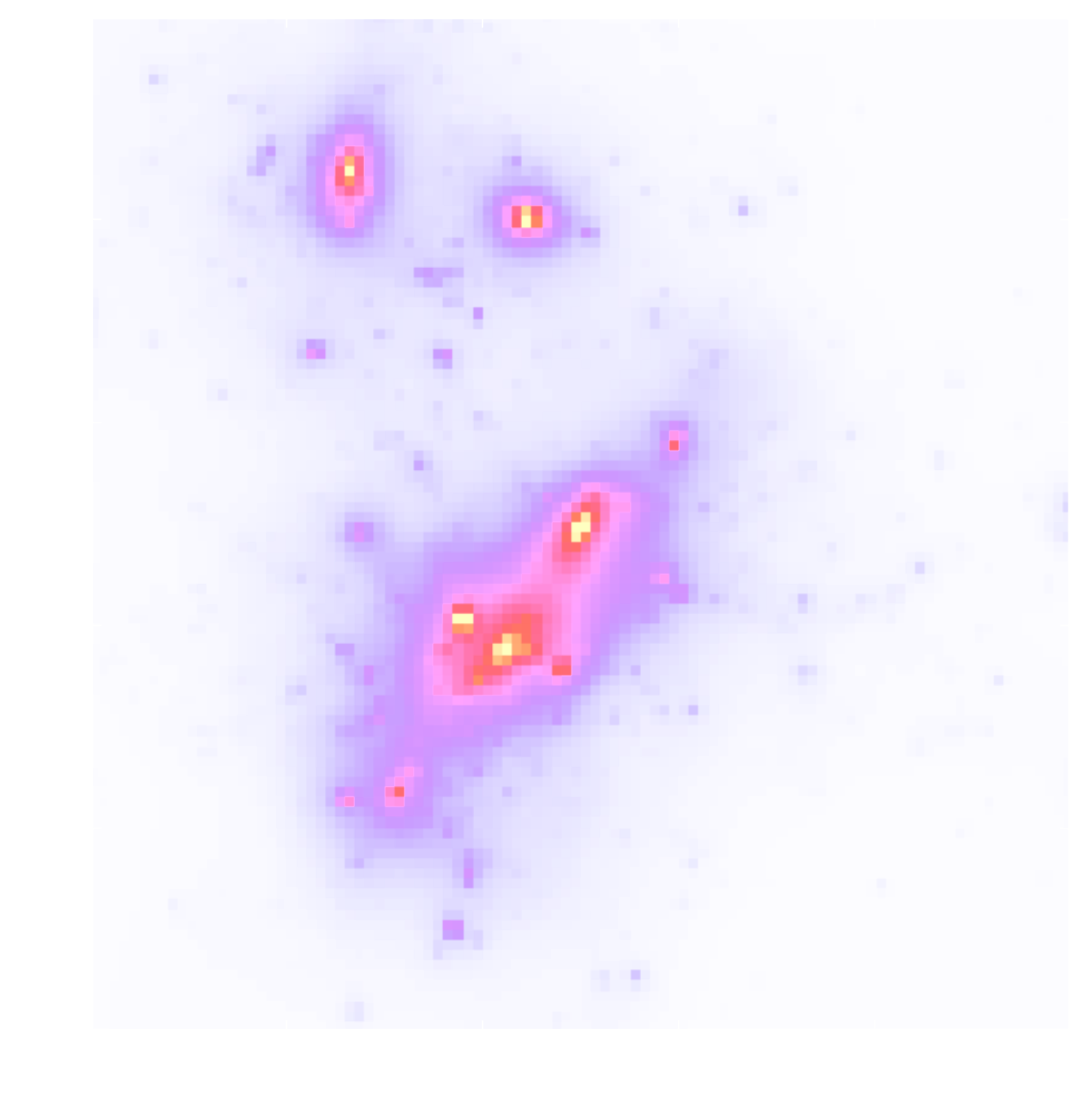
Pires, Starck, Amara, Réfrégier, and R. Teyssier (2009)
Wavelet peak counting statistics


There still an entire industry today of handcrafting summary statistics (see Ajani et al. 2023):

one-point PDF, peak counts, Minkowski functionals, Betti numbers, persistent homology Betti numbers and heatmap, and scattering transform coefficients...

Traditional work on handcrafted summary statistics had plateaued because of two major limitations




  • Handcrafted summaries can be more powerful than the power spectrum,
    but never guaranteed to be optimal (sufficient).



  • It is impossible to analytically model the likelihood of complex, non-linear summary statistics



$\Longrightarrow$ Until Deep Learning Changed The Game!

First Realisation: Summaries can be learned instead of handcrafted

Ravanbakhsh, Oliva, Fromenteau, Price, Ho, Schneider, Poczos (2017)

Second Realisation: Proper Inference with Simulators is possible

Cranmer, Pavez, Louppe (2015)
$$ r(\bf{x}; \theta_0, \theta_1) = \frac{p(\bf{x} | \theta_0)}{p(\bf{x} | \theta_1)} $$ can be estimated by training a classifier to distinguish samples from $p(\bf{x} | \theta_0)$ and $p(\bf{x} | \theta_1)$.

Implicit Cosmological Inference

The land of Simulations and Neural Density Estimation

The alternative to theoretical likelihoods: Simulation-Based Inference

  • Instead of trying to analytically evaluate the likelihood of sub-optimal summary statistics, let us build a forward model of the full observables.
    $\Longrightarrow$ The simulator becomes the physical model.



Benefits of a forward modeling approach
  • Model the full information content of the data (aka "full field inference").

  • Easy to incorporate systematic effects.

  • Easy to combine multiple cosmological probes by joint simulations.

Why is it classicaly hard to do simulation-based inference?

The Challenge of Simulation-Based Inference
$$ p(x|\theta) = \int p(x, z | \theta) dz = \int p(x | z, \theta) p(z | \theta) dz $$ Where $z$ are stochastic latent variables of the simulator.

$\Longrightarrow$ This marginal likelihood is intractable!

Black-box Simulators Define Implicit Distributions

  • A black-box simulator defines $p(x | \theta)$ as an implicit distribution, you can sample from it but you cannot evaluate it.
  • This gives us a procedure to sample from the Bayesian joint distribution $p(x, \theta)$: $$(x, \theta) \sim p(x | \theta) \ p(\theta)$$
  • Key Idea: Use a parametric distribution model to approximate an implicit distribution.
    • Neural Likelihood Estimation: $\mathcal{L} = - \mathbb{E}_{(x,\theta)}\left[ \log p_\phi( x | \theta ) \right] $

    • Neural Posterior Estimation: $\mathcal{L} = - \mathbb{E}_{(x,\theta)}\left[ \log p_\phi( \theta | x ) \right] $

    • Neural Ratio Estimation: $\mathcal{L} = - \mathbb{E}_{\begin{matrix} (x,\theta)~p(x,\theta) \\ \ \theta^\prime \sim p(\theta) \end{matrix}} \left[ \log r_\phi(x,\theta) + \log(1 - r_\phi(x, \theta^\prime)) \right] $

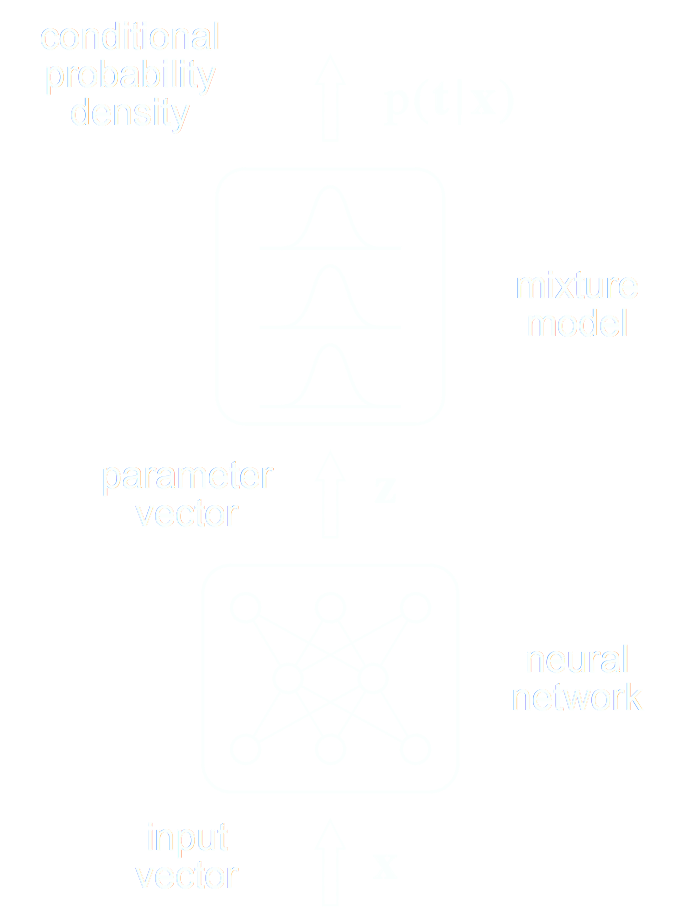
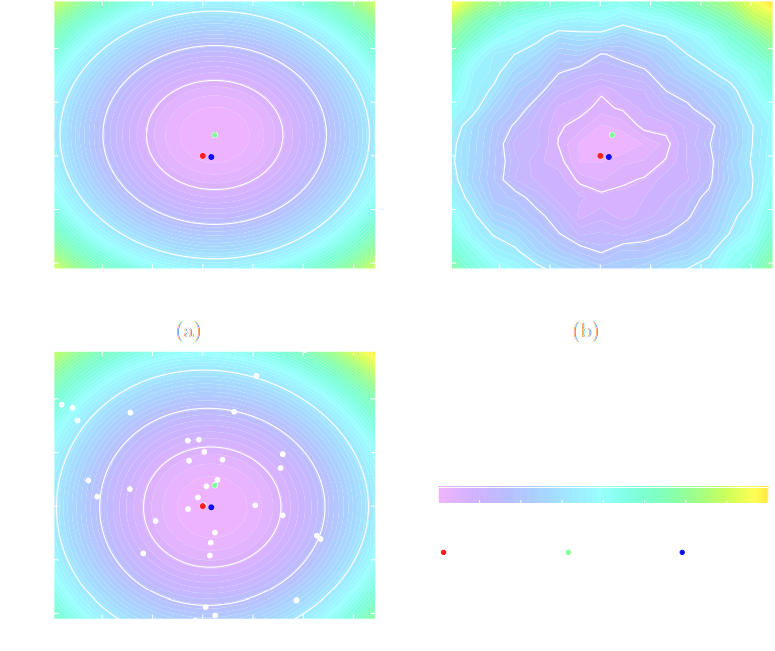
A closer look at Neural Posterior Estimation (NPE)

  • Building conditional neural density estimators $q_\phi(\theta | x)$ to approximate the posterior
    Bishop (1994)
  • Bounding the KL divergence between true and approximate posterior

    $$D_{KL}(p(\theta | x) ||q_\phi(\theta | x)) = \mathbb{E}_{\theta \sim p(\theta |x)} \left[ \log \frac{p(\theta | x)}{q_\phi(\theta | x)} \right] \geq 0 $$
    $$ \leq \mathbb{E}_{x \sim p(x)} \mathbb{E}_{\theta \sim p(\theta |x)} \left[ \log \frac{p(\theta | x)}{q_\phi(\theta | x)} \right] $$
    $$ \leq \boxed{ \mathbb{E}_{(x,\theta) \sim p(x, \theta)} \left[ - \log q_\phi(\theta | x) \right] } + cst $$


    $\Longrightarrow$ Minimizing the Negative Log Likelihood (NLL) over the joint distribution $p(x, \theta)$ leads to minimizing the KL divergence between the model posterior $q_{\phi}(\theta|x)$ and true posterior $p(\theta | x)$.


We have converged to a standard SBI recipe


A two-steps approach to Implicit Inference
  • Automatically learn an optimal low-dimensional summary statistic $$y = f_\varphi(x) $$
  • Use Neural Density Estimation to either:
    • build an estimate $p_\phi$ of the likelihood function $p(y \ | \ \theta)$ (Neural Likelihood Estimation)

    • build an estimate $p_\phi$ of the posterior distribution $p(\theta \ | \ y)$ (Neural Posterior Estimation)

Information Point of View on Neural Summarisation



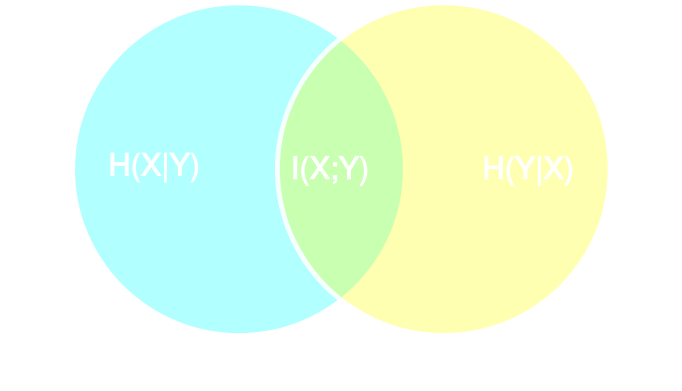
Learning Sufficient Statistics
  • Summary statistics $y$ is sufficient for $\theta$ if $$ I(Y; \Theta) = I(X; \Theta) \Leftrightarrow p(\theta | x ) = p(\theta | y) $$
  • Variational Mutual Information Maximization $$ \mathcal{L} \ = \ \mathbb{E}_{x, \theta} [ \log q_\phi(\theta | y=f_\varphi(x)) ] \leq I(Y; \Theta) $$ (Barber & Agakov variational lower bound)
    Jeffrey, Alsing, Lanusse (2021)

Another Approach: maximizing the Fisher information

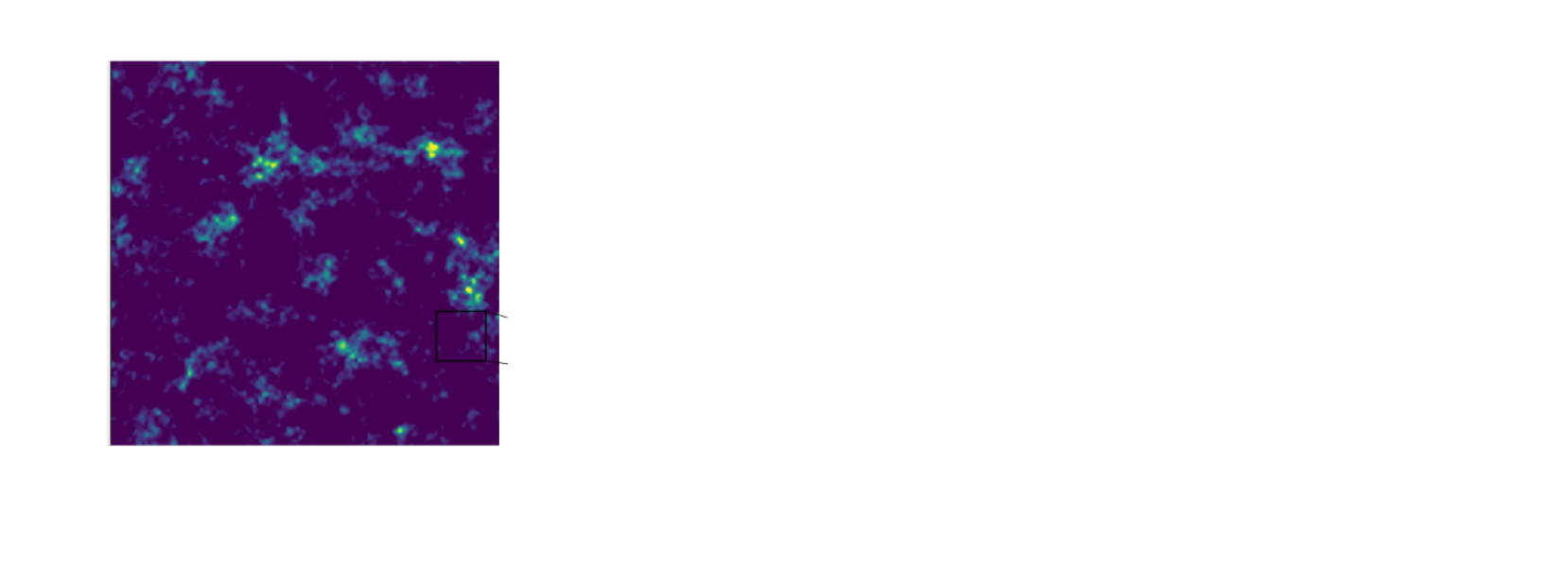Information Maximization Neural Network (IMNN) $$\mathcal{L} \ = \ - | \det \mathbf{F} | \ \mbox{with} \ \mathbf{F}_{\alpha, \beta} = tr[ \mu_{\alpha}^t C^{-1} \mu_{\beta} ] $$
Charnock, Lavaux, Wandelt (2018)

People use a lot of variants in practice!


* grey rows are papers analyzing survey data

Optimal Neural Summarisation for Cosmological Implicit Inference

Lanzieri, Zeghal et al. (2024)
  • Asymptotically VMIM yields a sufficient statistics
    • No reason not to use it in practice, it works well, and is asymptotically optimal



  • Mean Squared Error (MSE) DOES NOT yield a sufficient statistics even asymptotically
    • Same for Mean Absolute Error (MAE) and weighted versions of MSE

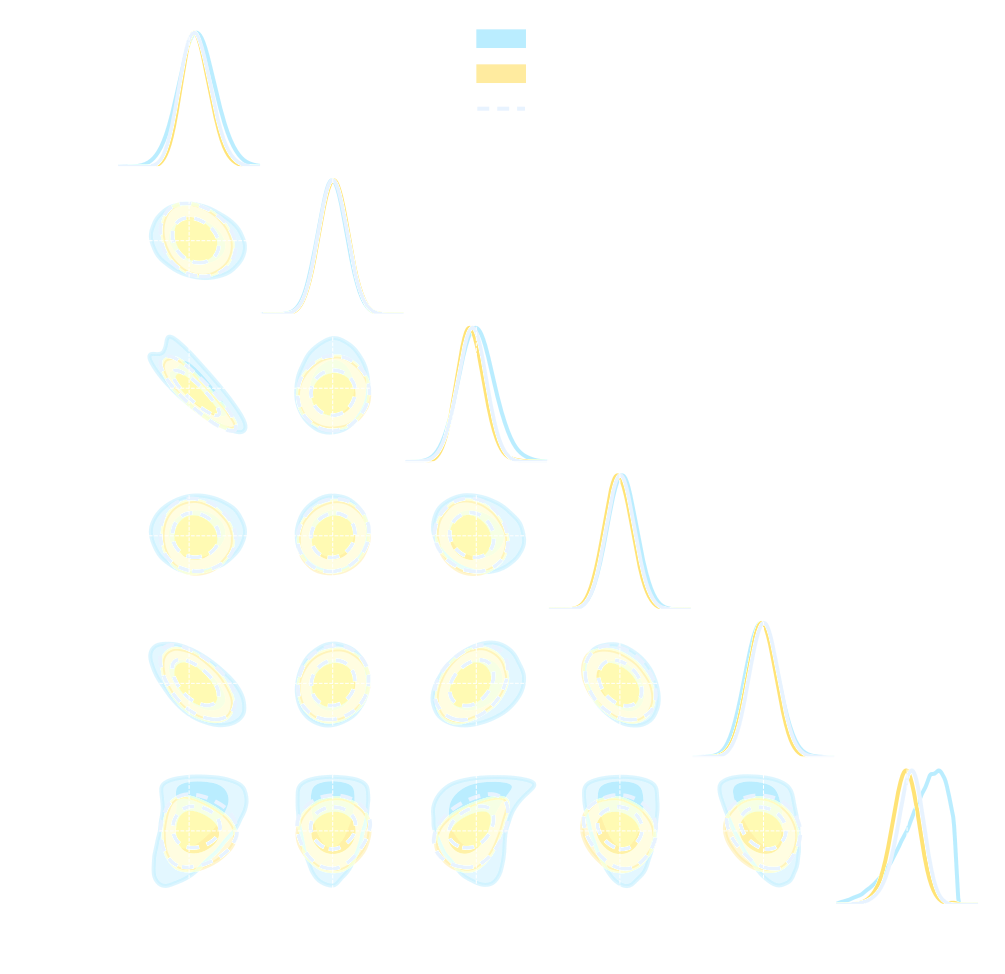
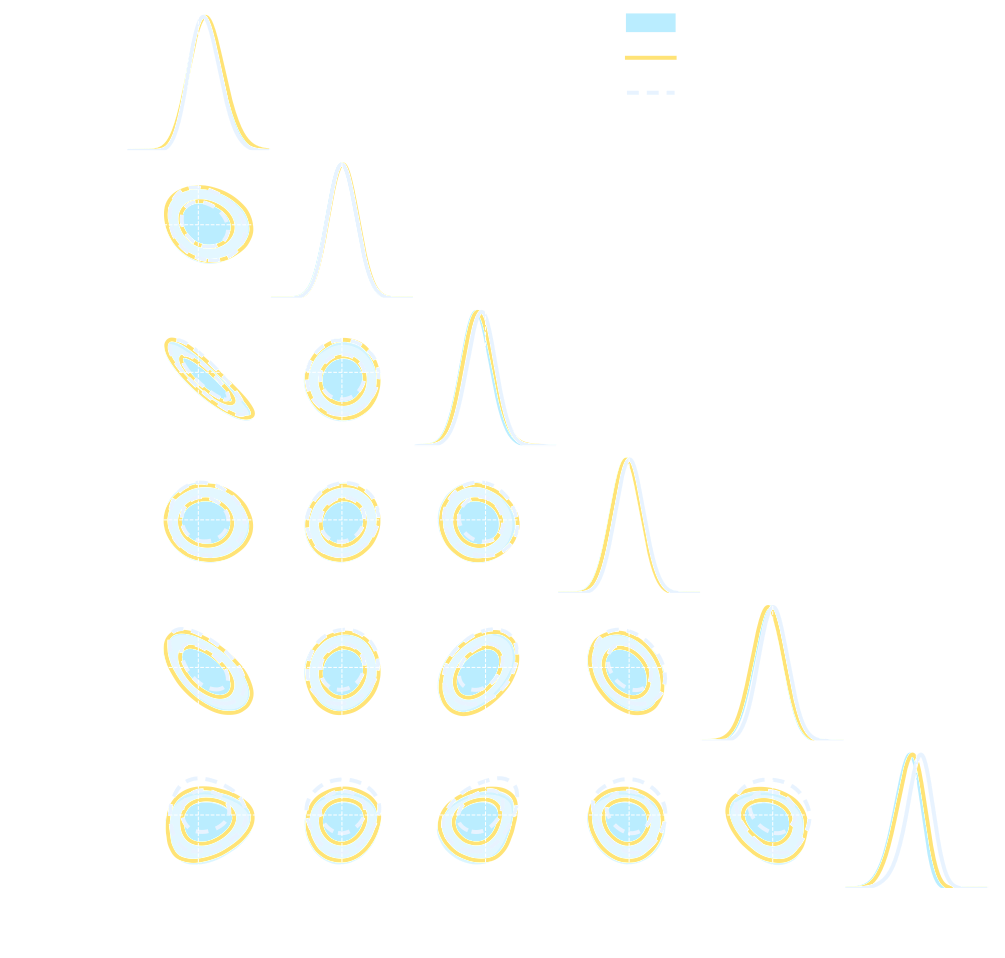
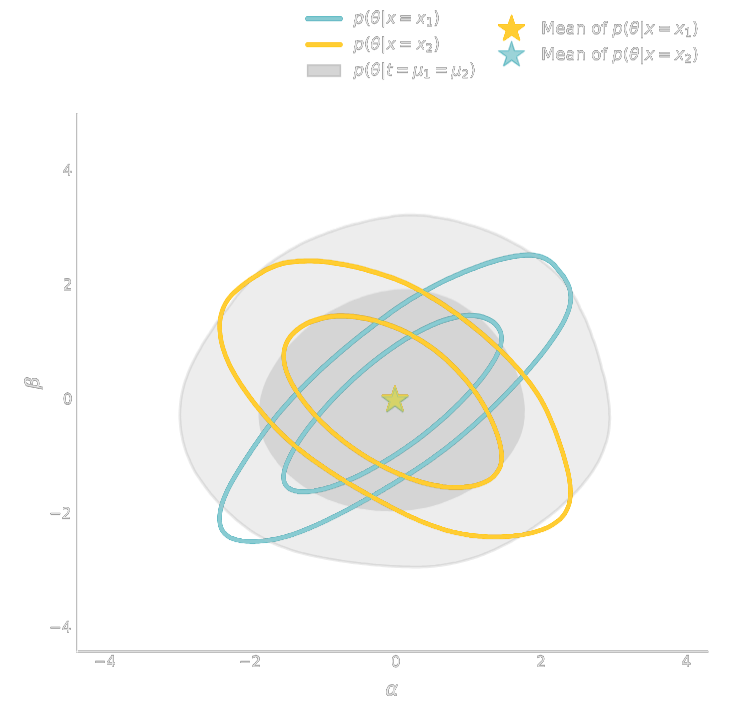
credit: Justine Zeghal

Our humble beginnings: Likelihood-Free Parameter Inference with DES SV...

Jeffrey, Alsing, Lanusse (2021)

Suite of N-body + raytracing simulations: $\mathcal{D}$

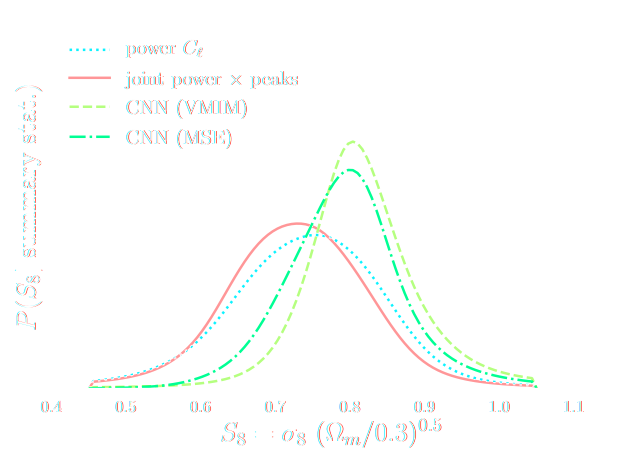
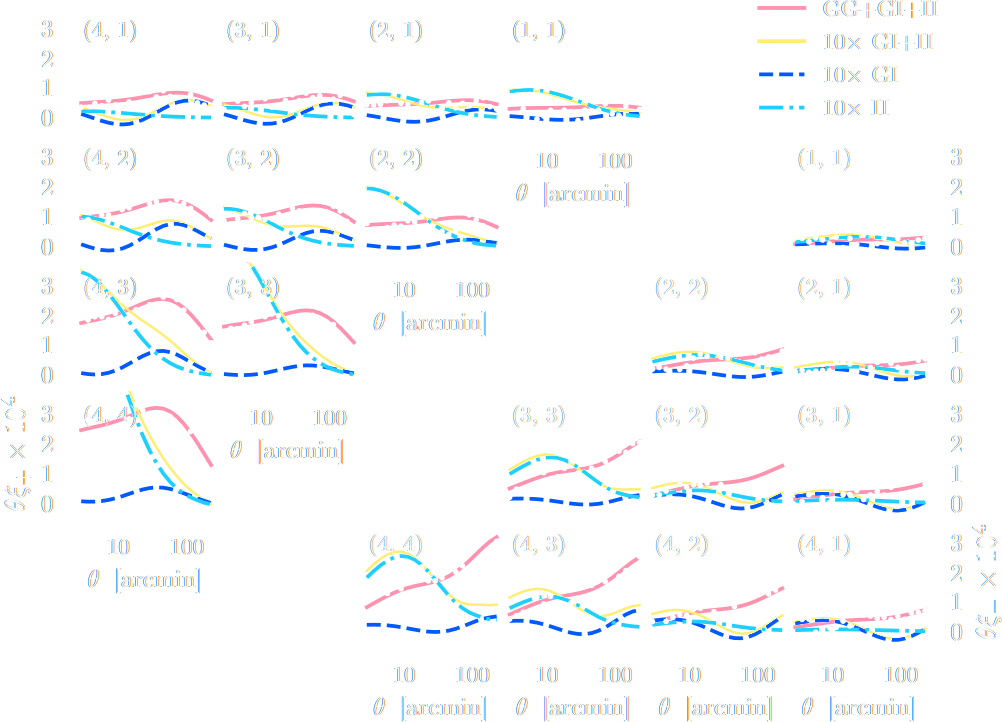
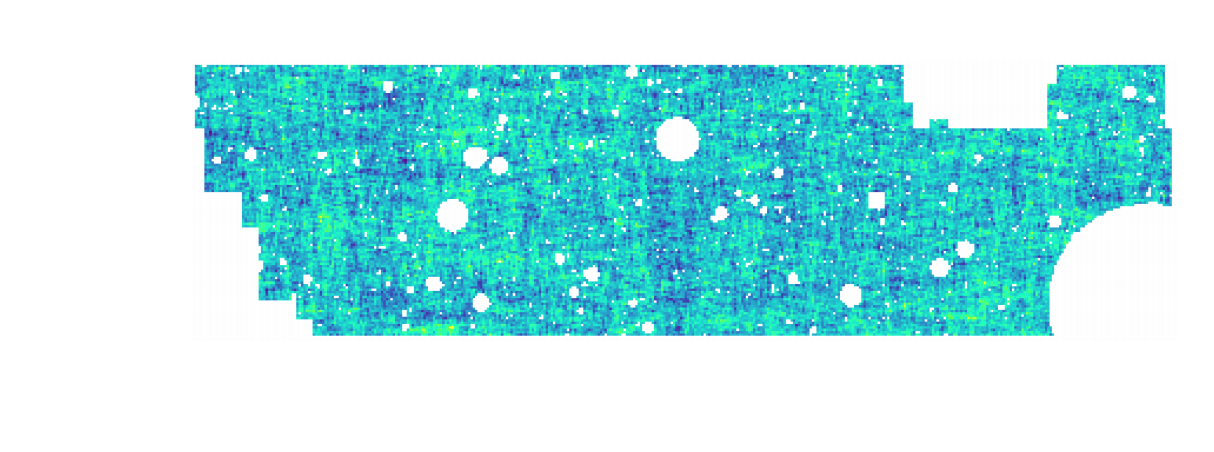
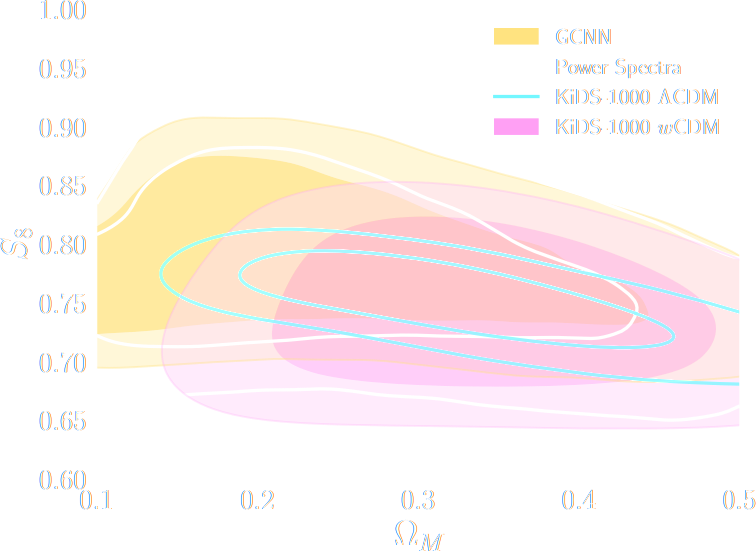
$w$CDM analysis of KiDS-1000 Weak Lensing (Fluri et al. 2022)

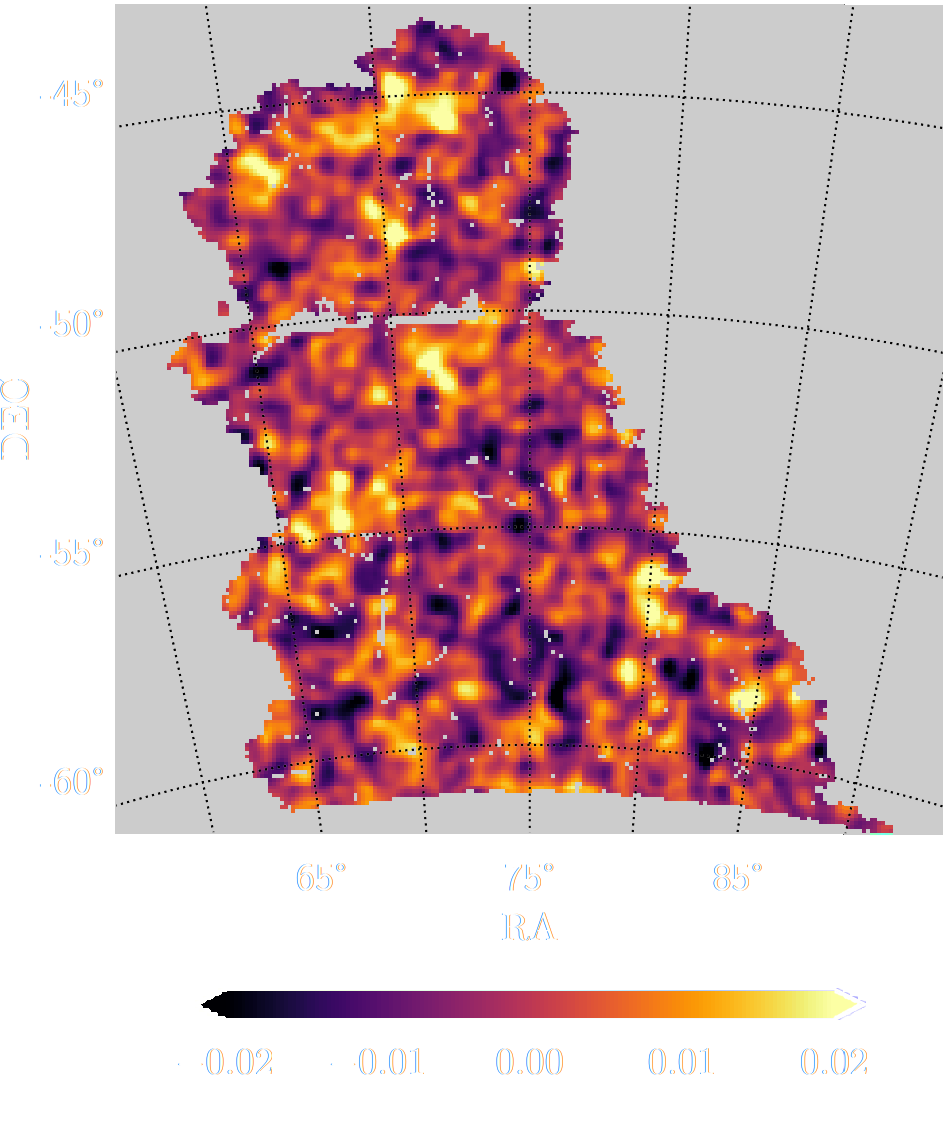
Fluri, Kacprzak, Lucchi, Schneider, Refregier, Hofmann (2022)


KiDS-1000 footprint and simulated data
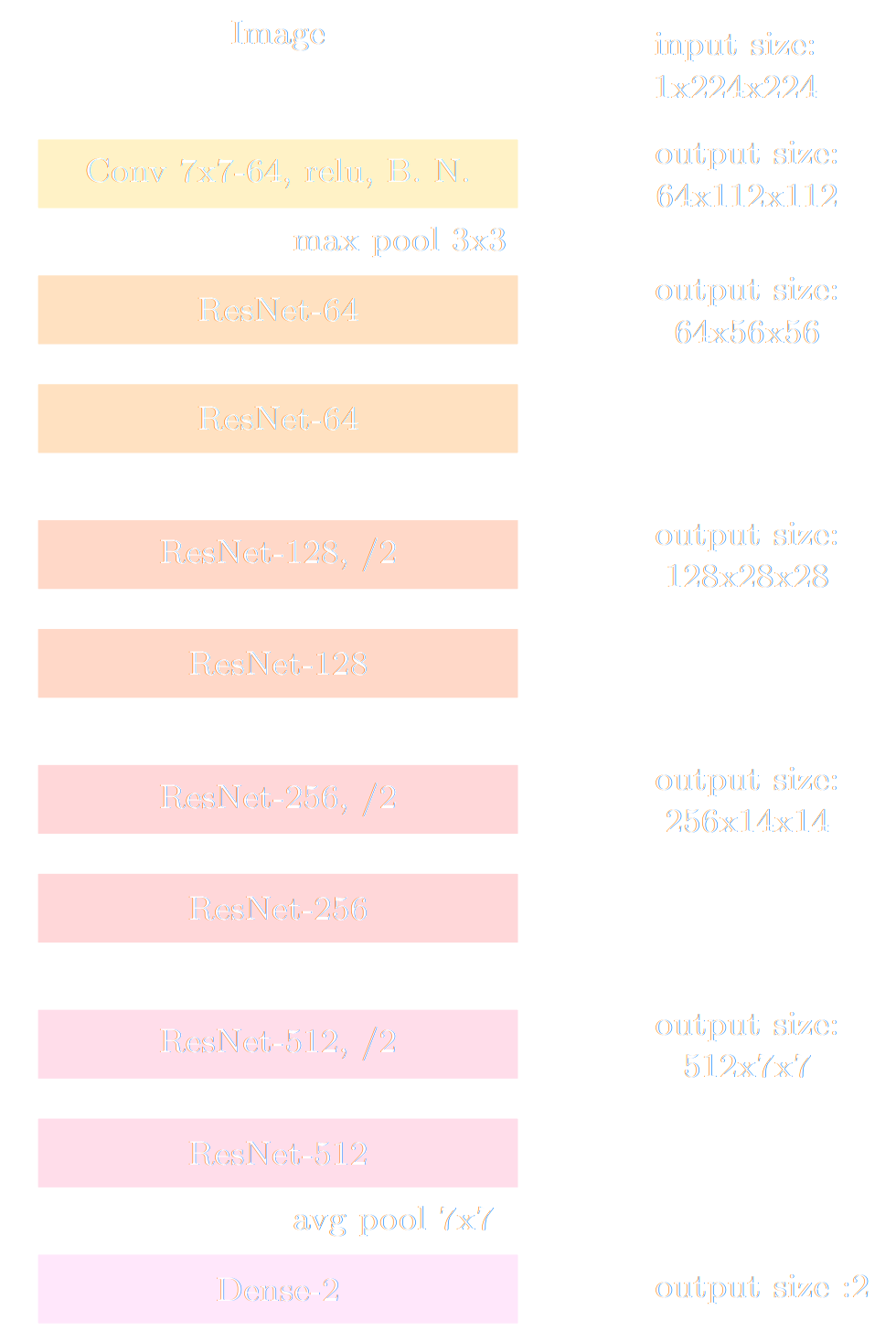
  • Neural Compressor: Graph Convolutional Neural Network on the Sphere
    Trained by Fisher information maximization.

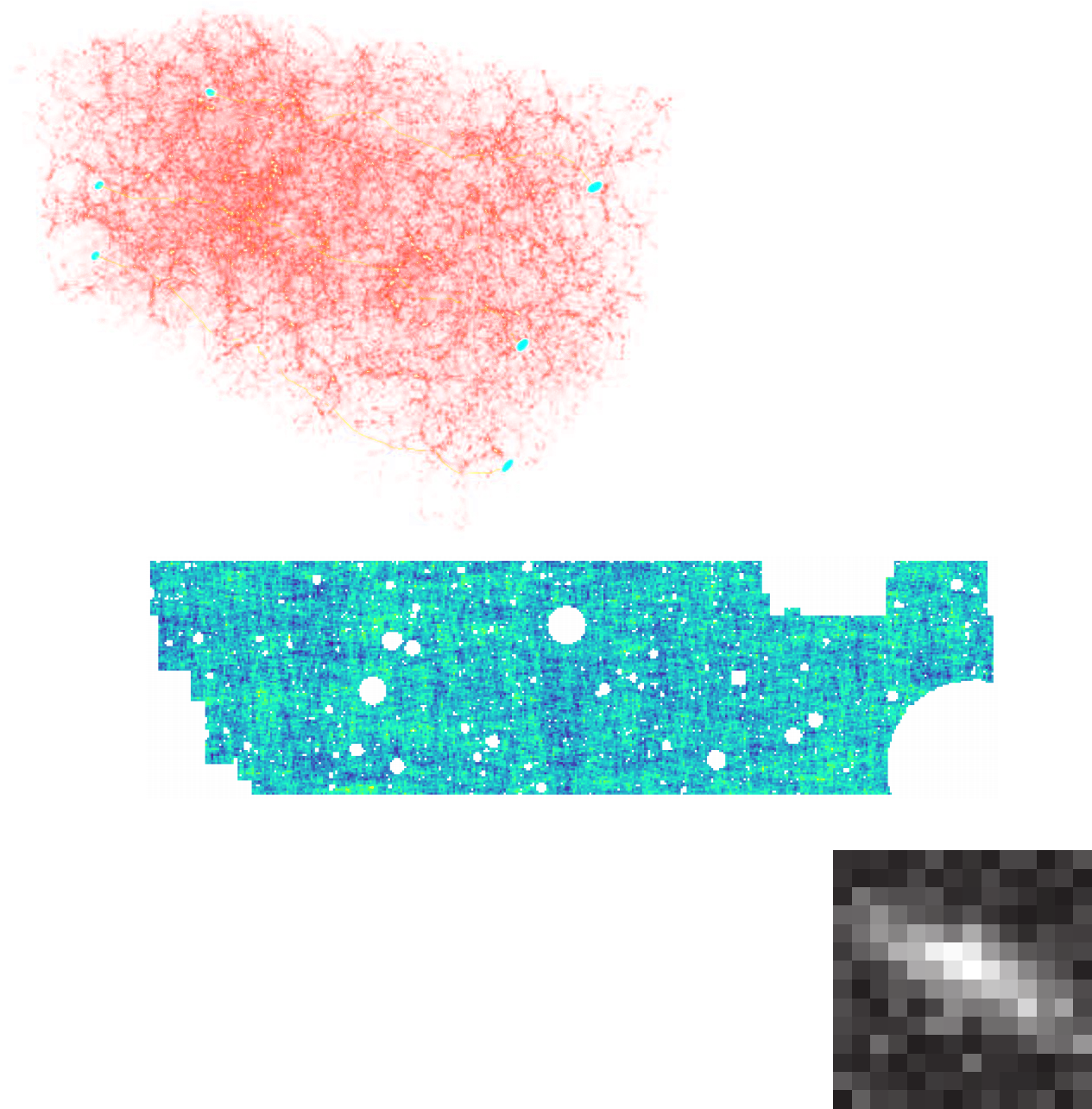
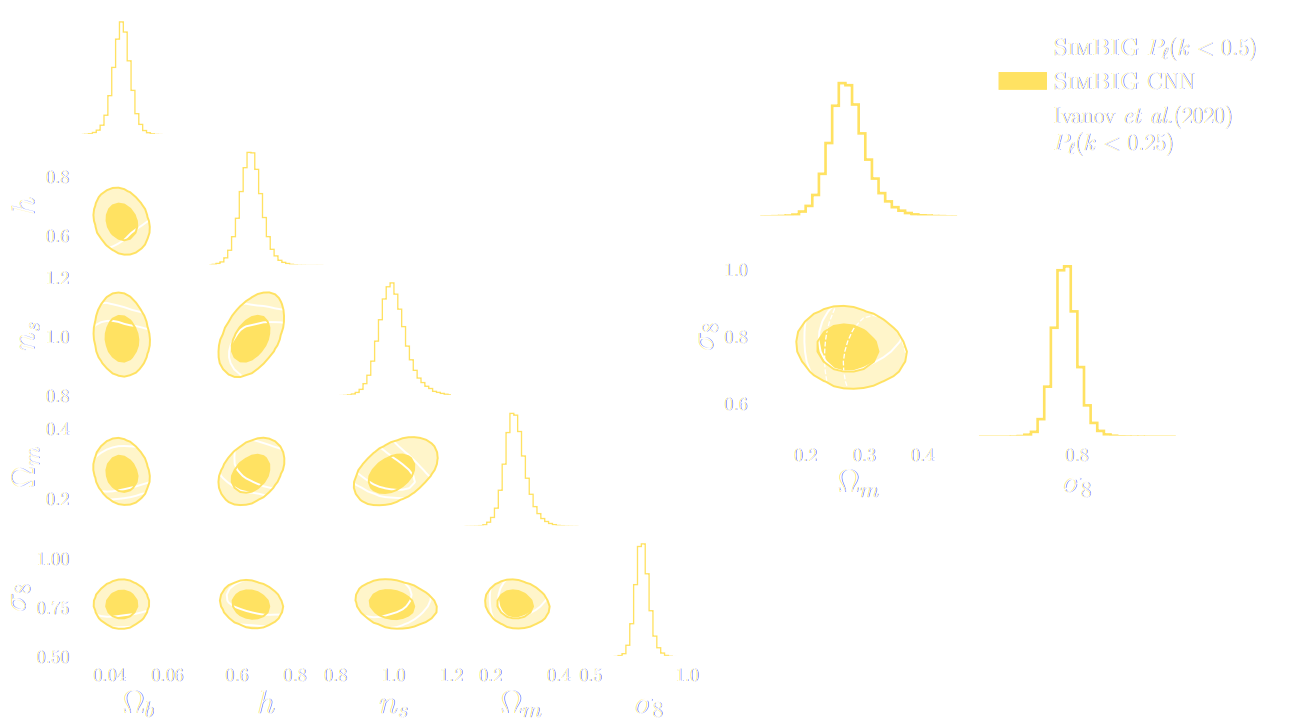
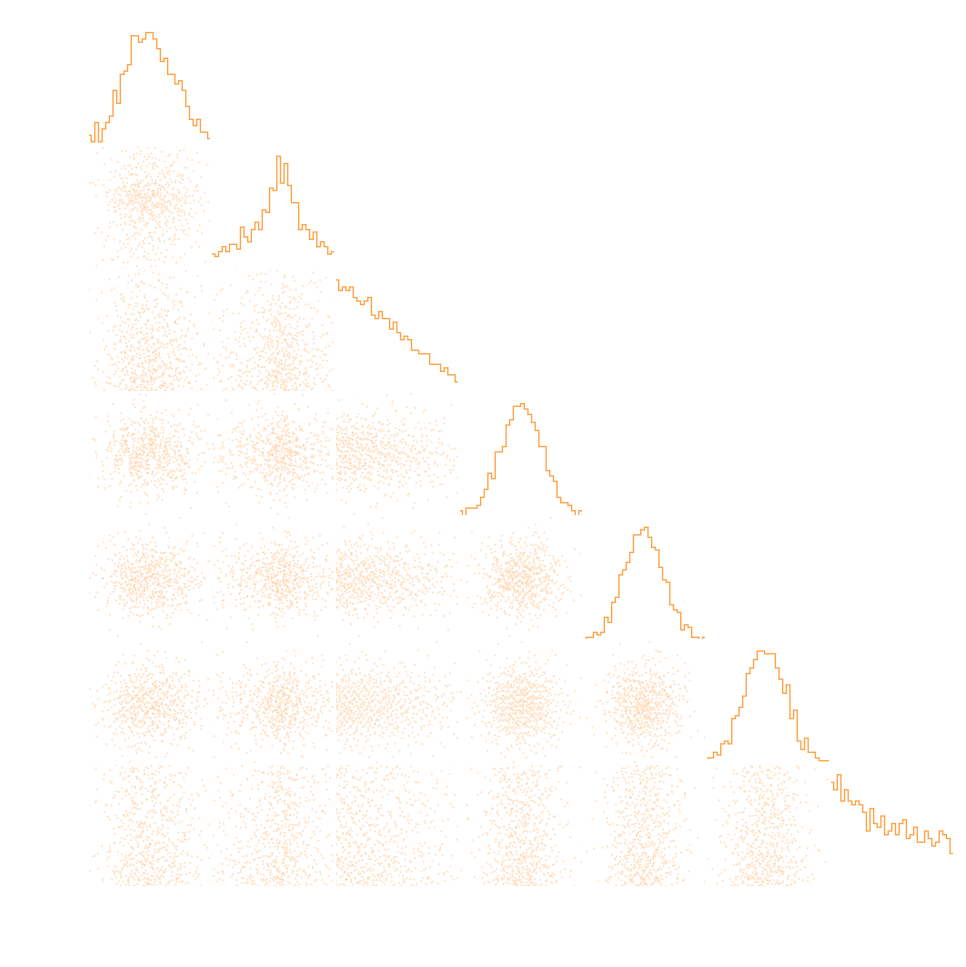
SIMBIG: Field-level SBI of Large Scale Structure (Lemos et al. 2023)



















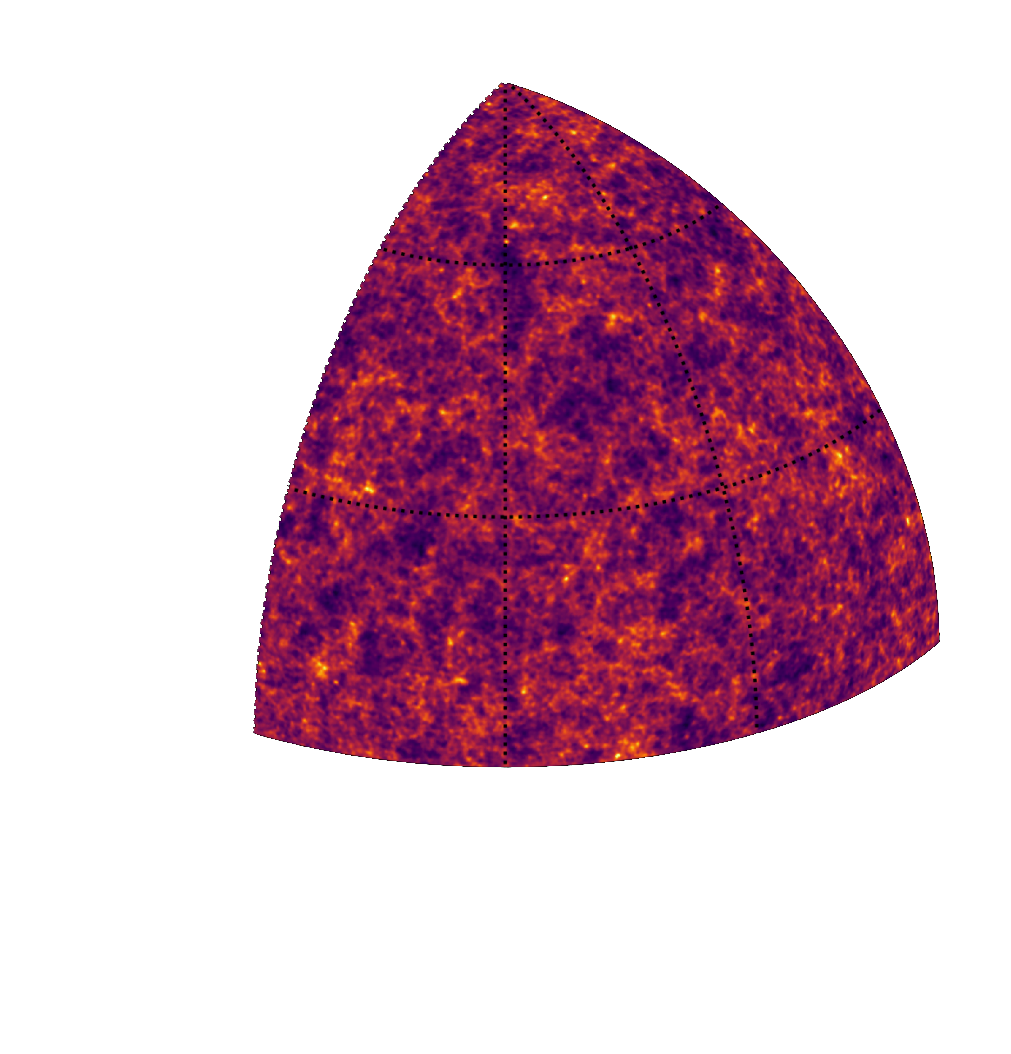
BOSS CMASS galaxy sample: Data vs Simulations
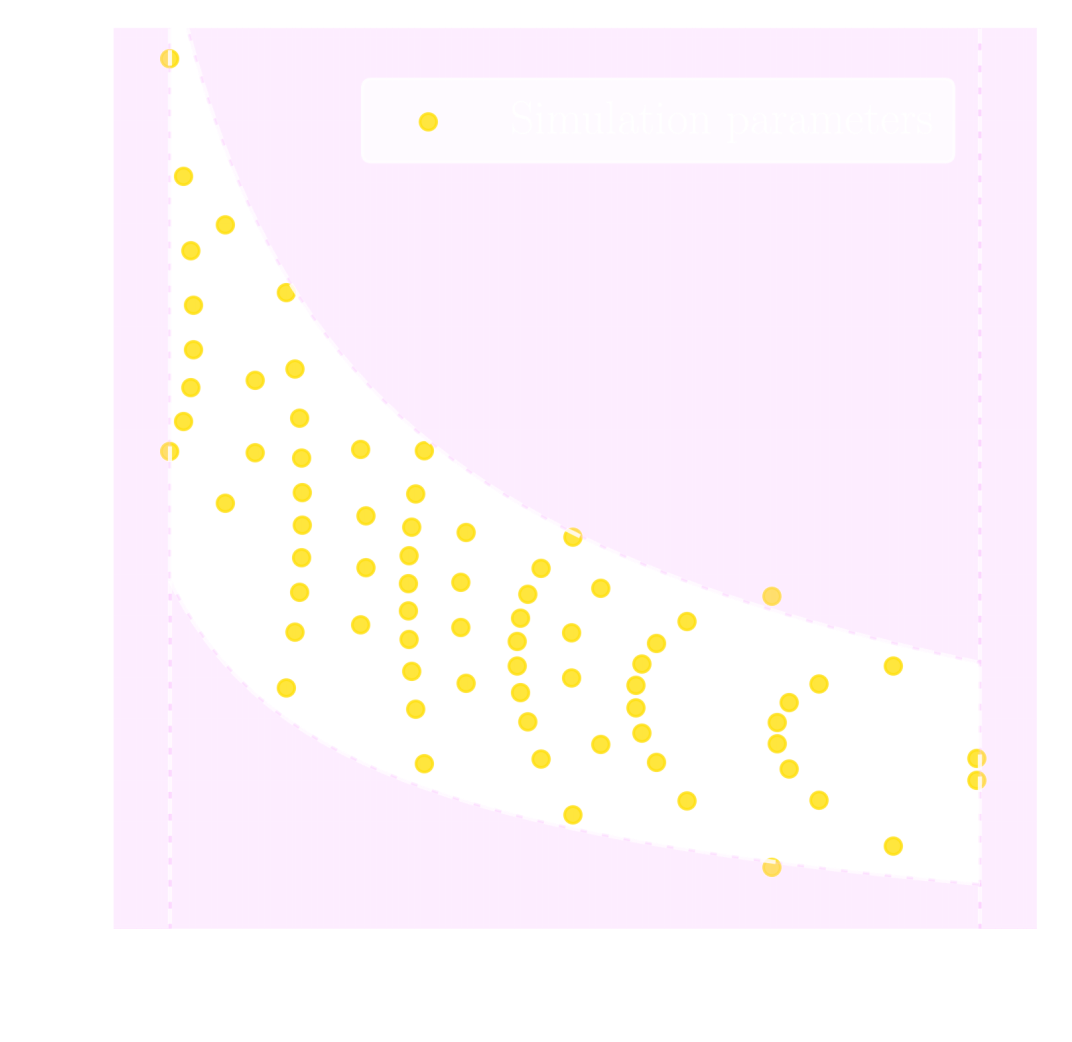
  • 20,000 simulated galaxy samples at 2,000 cosmologies
Hahn et al. (2022)

Finally, SBI has reached the mainstream: Official DES year 3 SBI wCDM results

Jeffrey et al. (2024)




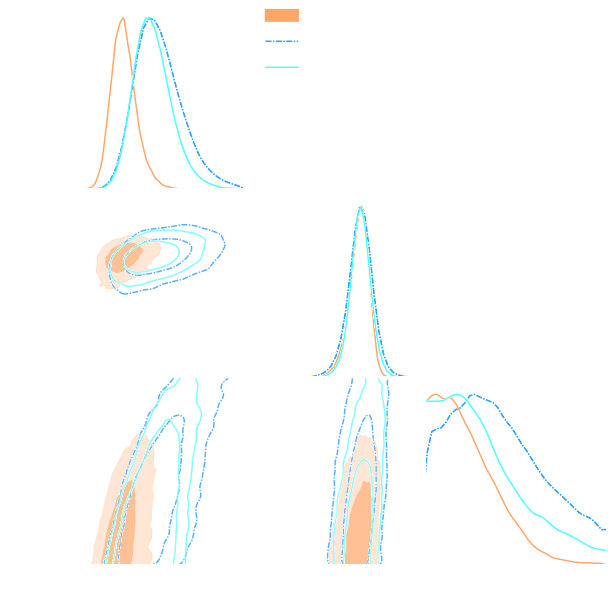
Alright, so, we know how to do SBI...

Has it delivered everything we hoped for?

Example of unforeseen impact of shortcuts in simulations

Gatti, Jeffrey, Whiteway et al. (2023)

Is it ok to distribute lensing source galaxies randomly in simulations, or should they be clustered?

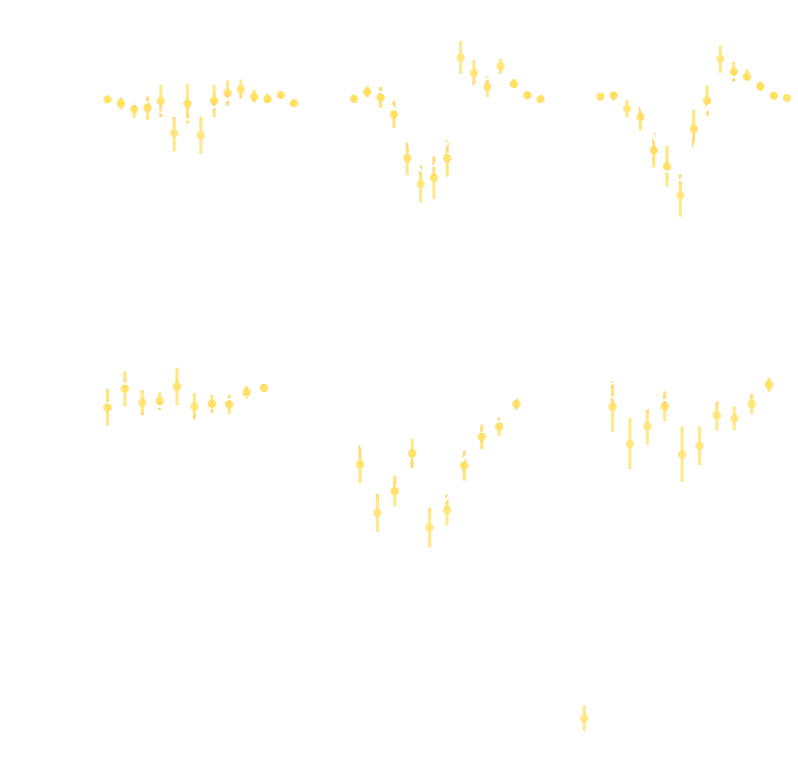
$\Longrightarrow$ An SBI analysis could be biased by this effect and you would never know it!

How much usable information is there beyond the power spectrum?

Chisari et al. (2018)

Ratio of power spectrum in hydrodynamical simulations vs. N-body simulations
Secco et al. (2021)

DES Y3 Cosmic Shear data vector

$\Longrightarrow$ Can we find non-Gaussian information that is not affected by baryons?

takeways and motivations for a Challenge


Will we be able to exploit all of the information content of LSST, Euclid, DESI?
$\Longrightarrow$ Not rightaway, but it is not the fault of the inference methodology!

  • Deep Learning has redefined the limits of our statistical tools, creating additional demand on the accuracy of simulations far beyond the power spectrum.

  • Neural compression methods have the downside of being opaque. It is much harder to detect unknown systematics.

  • We will need a significant number of large volume, high resolution simulations.

What the NeurIPS 2025 Fair Universe Challenge will teach us:

  • Phase I: Strategies for training neural summary statistics with very few simulations

  • Phase II: Strategies for robustness to unknown model mispecification

And finally, on a personal note, the stakes have never been higher!

Will the machines take over my line of work?


Stay tuned for the results!