Implicit and Explicit Simulation-Based Bayesian Inference for Cosmology

François Lanusse










slides at eiffl.github.io/talks/Prague2023

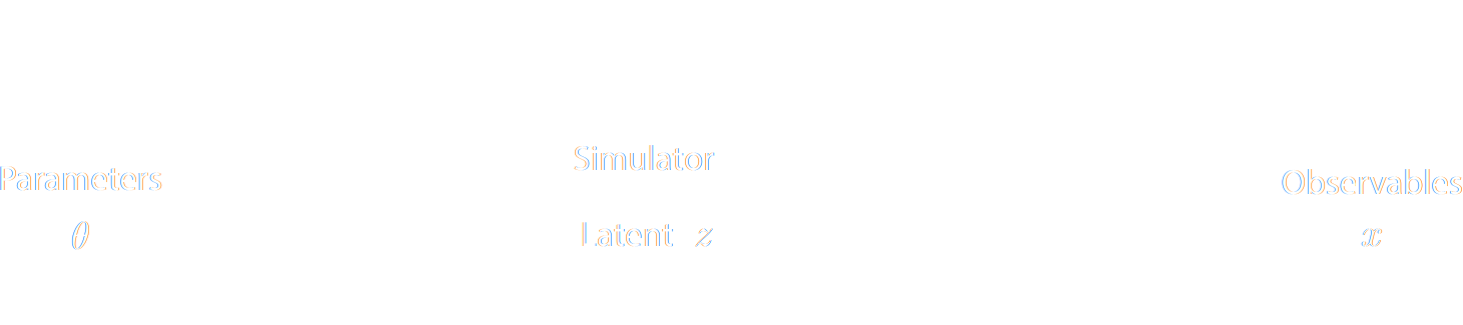
Full-Field Inference

  • Instead of analytically evaluating the likelihood of sub-optimal summary statistics, let us build a model of the full observables.
    $\Longrightarrow$ The simulator becomes the physical model.

  • Each component of the full probabilistic model of the observables is now tractable, but at the cost of a large number of latent variables.


Benefits of a forward modeling approach
  • Fully exploits the information content of the data (aka "full field inference").

  • Easy to incorporate systematic effects.

  • Easy to combine multiple cosmological probes by joint simulations.
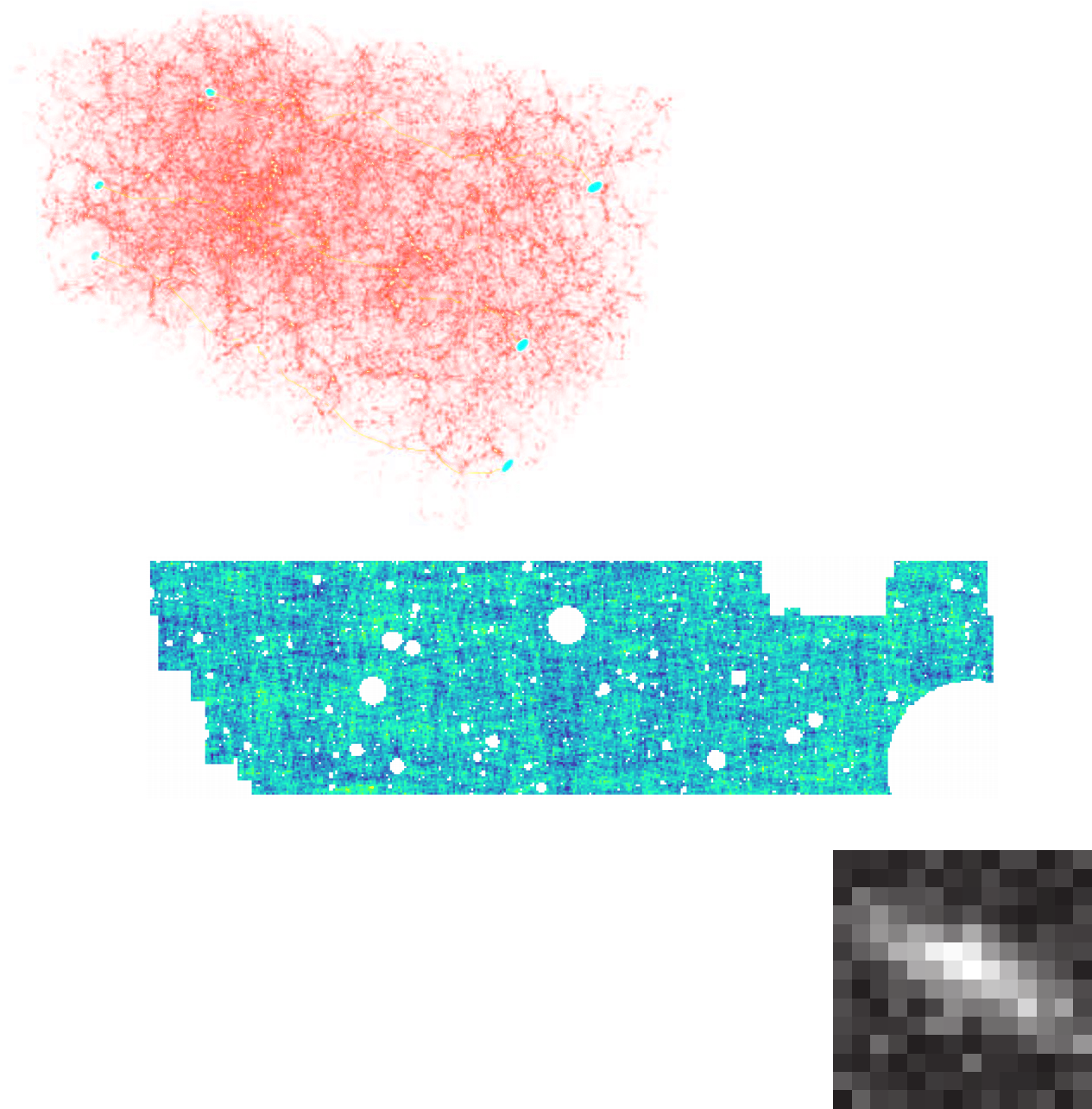
(Porqueres et al. 2021)
For now, let's ignore the elephant in the room:
Do we have reliable enough models for the full complexity of the data?

...so why is this not mainstream?

The Challenge of Full-Field Inference
  • If we are interested in the likelihood $p(x | \theta)$ we need to marginalize over stochastic latent variables: $$ p(x|\theta) = \int p(x, z | \theta) dz = \int p(x | z, \theta) p(z | \theta) dz $$
  • If $x$ is the lensing angular power spectrum, this marginalization can be approximated analytically: $$p(C_\ell | \theta) \simeq \mathcal{N}(C_\ell; C_\ell^{th}, \Sigma)$$
  • If $x$ is e.g. a full shear map, this marginalization is analytically intractable.
    $\Longrightarrow$ We need to find a tractable way to compute the marginal likelihood $p(x|\theta)$.


How to perform inference over forward simulation models?

  • Implicit Inference: Treat the simulator as a black-box with only the ability to sample from the joint distribution $$(x, \theta) \sim p(x, \theta)$$ a.k.a.
    • Simulation-Based Inference (SBI)
    • Likelihood-free inference (LFI)
    • Approximate Bayesian Computation (ABC)

  • Explicit Inference: Treat the simulator as a probabilistic model and perform inference over the joint posterior $$p(\theta, z | x) \propto p(x | z, \theta) p(z, \theta) p(\theta) $$ a.k.a.
    • Bayesian Hierarchical Modeling (BHM)

$\Longrightarrow$ For a given simulation model, both methods should converge to the same posterior!

Implicit Inference

The land of Neural Density Estimation

Black-box Simulators Define Implicit Distributions

  • A black-box simulator defines $p(x | \theta)$ as an implicit distribution, you can sample from it but you cannot evaluate it.
  • Key Idea: Use a parametric distribution model $\mathbb{P}_\varphi$ to approximate the implicit distribution $\mathbb{P}$.

True $\mathbb{P}$

Samples $x_i \sim \mathbb{P}$

Model $\mathbb{P}_\varphi$
  • Once trained, you can typically sample from $\mathbb{P}_\varphi$ and/or evaluate the likelihood $p_\varphi(x | \theta)$.

Conditional Density Estimation with Neural Networks

  • I assume a forward model of the observations: \begin{equation} p( x ) = p(x | \theta) \ p(\theta) \nonumber \end{equation} All I ask is the ability to sample from the model, to obtain $\mathcal{D} = \{x_i, \theta_i \}_{i\in \mathbb{N}}$

  • I am going to assume $q_\phi(\theta | x)$ a parametric conditional density

  • Optimize the parameters $\phi$ of $q_{\phi}$ according to \begin{equation} \min\limits_{\phi} \sum\limits_{i} - \log q_{\phi}(\theta_i | x_i) \nonumber \end{equation} In the limit of large number of samples and sufficient flexibility \begin{equation} \boxed{q_{\phi^\ast}(\theta | x) \approx p(\theta | x)} \nonumber \end{equation}
$\Longrightarrow$ One can asymptotically recover the posterior by optimizing a parametric estimator over
the Bayesian joint distribution
$\Longrightarrow$ One can asymptotically recover the posterior by optimizing a Deep Neural Network over
a simulated training set.

A variety of algorithms

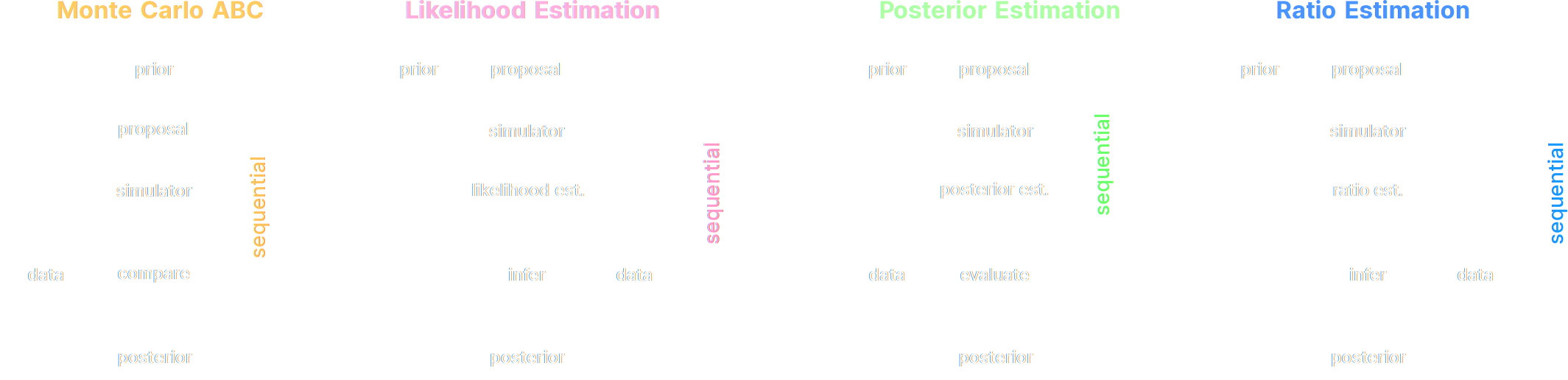
Lueckmann, Boelts, Greenberg, Gonçalves, Macke (2021)


A few important points:

  • Amortized inference methods, which estimate $p(\theta | x)$, can greatly speed up posterior estimation once trained.

  • Sequential Neural Posterior/Likelihood Estimation methods can actively sample simulations needed to refine the inference.

My Practical Recipe to Apply Neural Density Estimation

A two-steps approach to Likelihood-Free Inference
  • Step I Automatically learn a optimal low-dimensional summary statistic $$y = f_\varphi(x) $$ typically $y$ will have the same dimensionality as $\theta$.

  • Step II: Use Neural Density Estimation in low dimension to either:
    • build an estimate $p_\phi$ of the likelihood function $p(y \ | \ \theta)$ (Neural Likelihood Estimation)

    • build an estimate $p_\phi$ of the posterior distribution $p(\theta \ | \ y)$ (Neural Posterior Estimation)

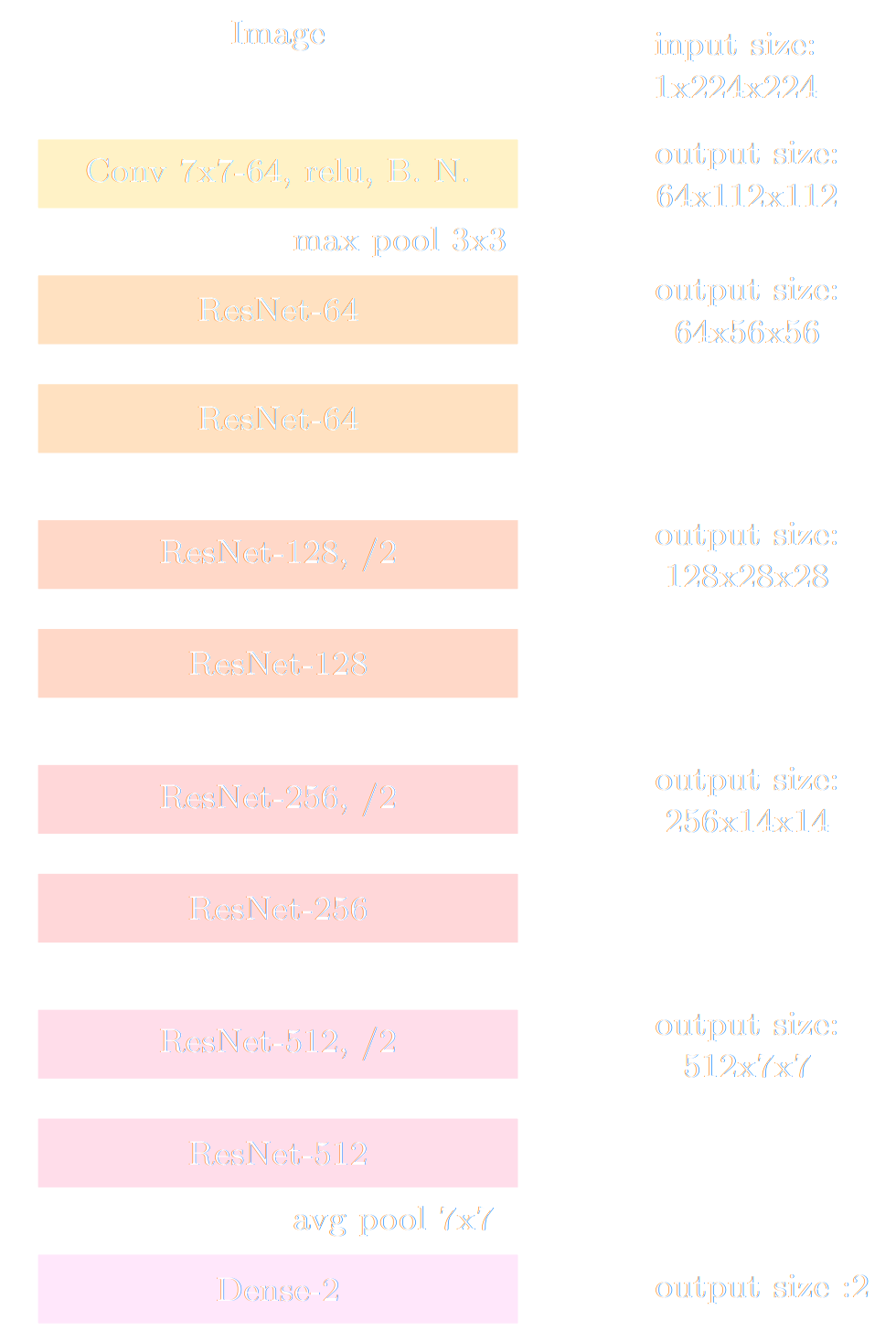
Automated Summary Statistics Extraction

  • Introduce a parametric function $f_\varphi$ to reduce the dimensionality of the data while preserving information.
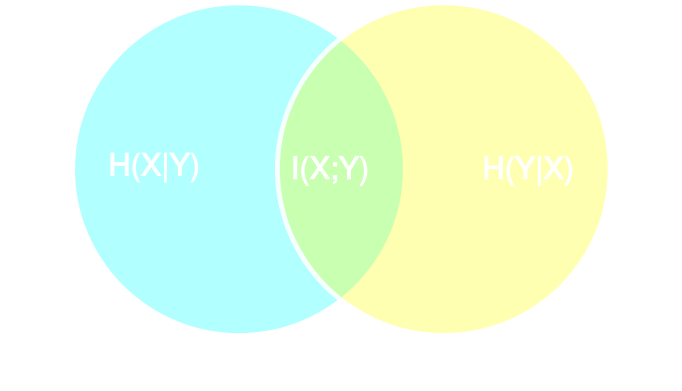
Information-based loss functions
  • Summary statistics $y$ is sufficient for $\theta$ if, and only if, $$ I(Y; \Theta) = I(X; \Theta) \Leftrightarrow p(\theta | x ) = p(\theta | y) $$
  • Variational Mutual Information Maximization $$ \mathcal{L} \ = \ \mathbb{E}_{x, \theta} [ \log q_\phi(\theta | f_\varphi(x)) ] \leq I(Y; \Theta) $$
    Jeffrey, Alsing, Lanusse (2021)

Example of application: Likelihood-Free parameter inference with DES SV

Jeffrey, Alsing, Lanusse (2021)

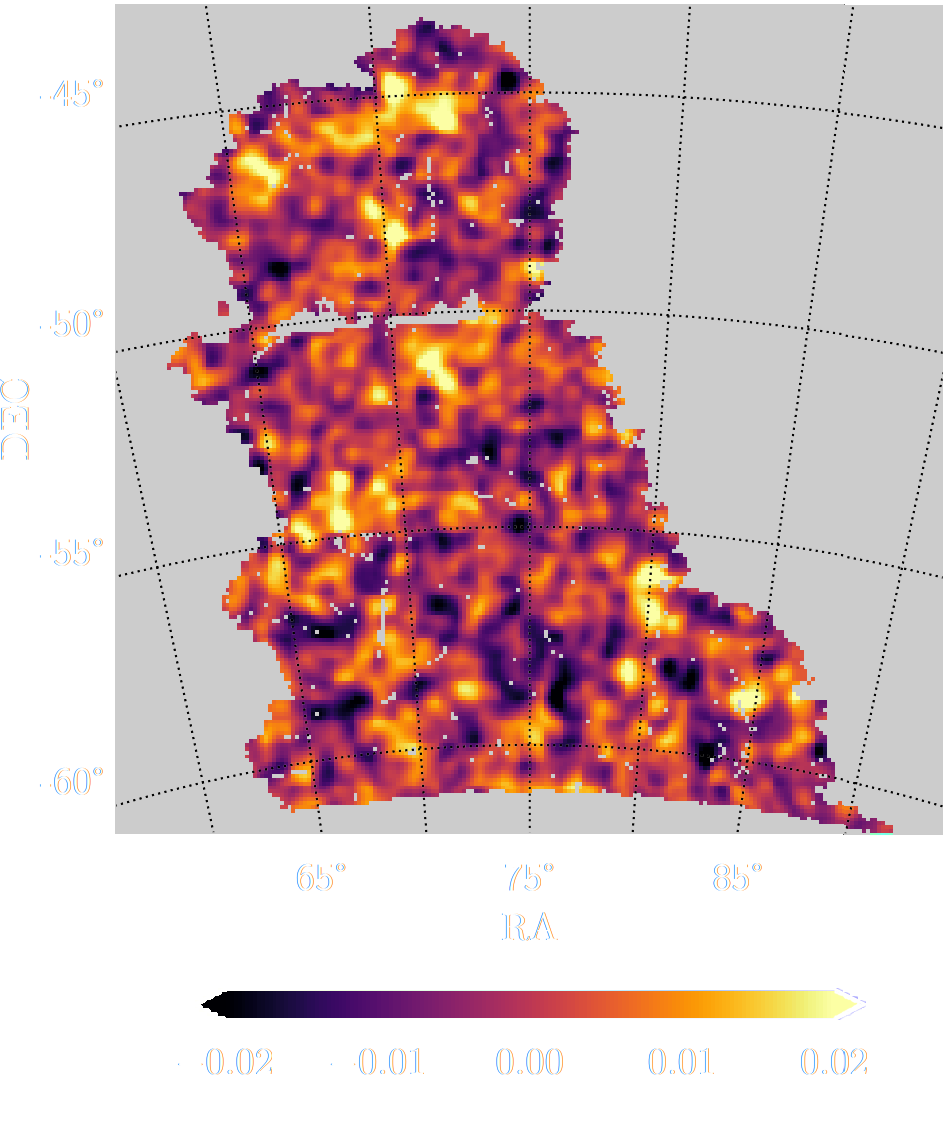
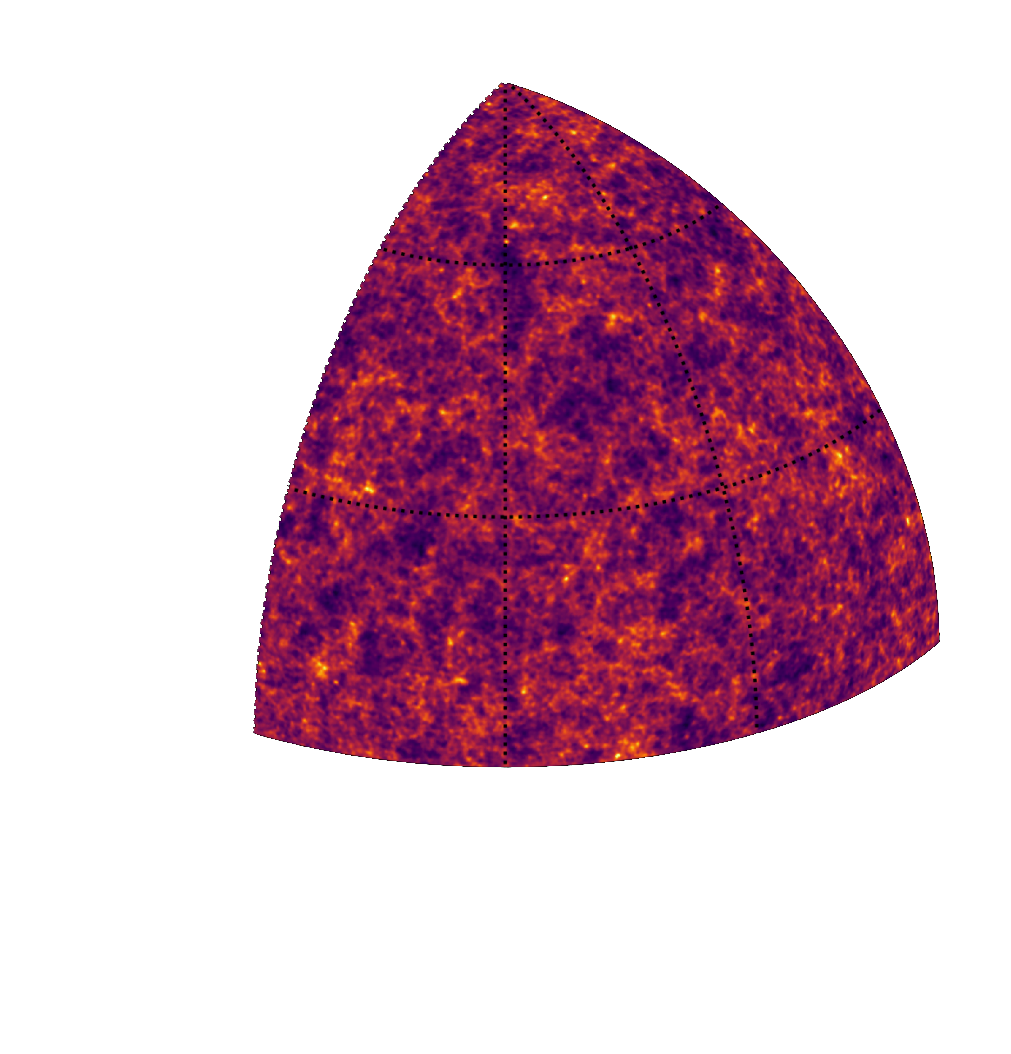
Suite of N-body + raytracing simulations: $\mathcal{D}$

Towards Optimal Full-Field Implicit Inference
by Neural Summarisation and Density Estimation

Open In Colab

Work led by Denise Lanzieri and Justine Zeghal




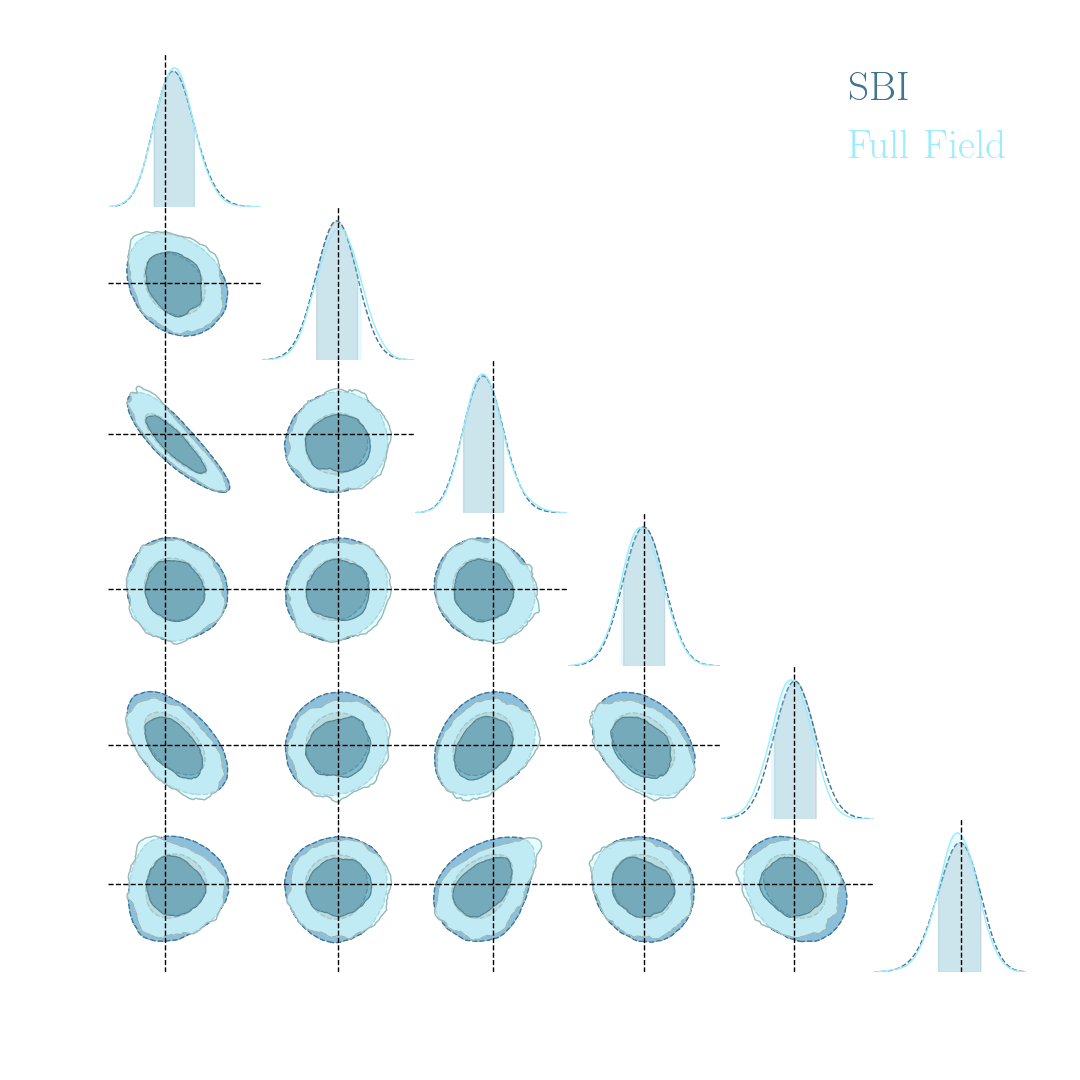
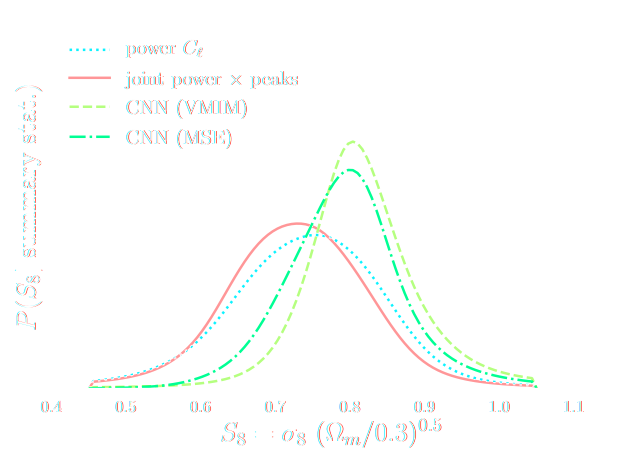
An easy-to-use validation testbed: log-normal lensing simulations


DifferentiableUniverseInitiative/sbi_lens
JAX-based log-normal lensing simulation package
  • 10x10 deg$^2$ maps at LSST Y10 quality, conditioning the log-normal shift parameter on $(\Omega_m, \sigma_8, w_0)$

  • Infer full-field posterior on cosmology:
    • explicitly using an Hamiltonian-Monte Carlo (NUTS) sampler
    • implicitly using a learned summary statistics and conditional density estimation.

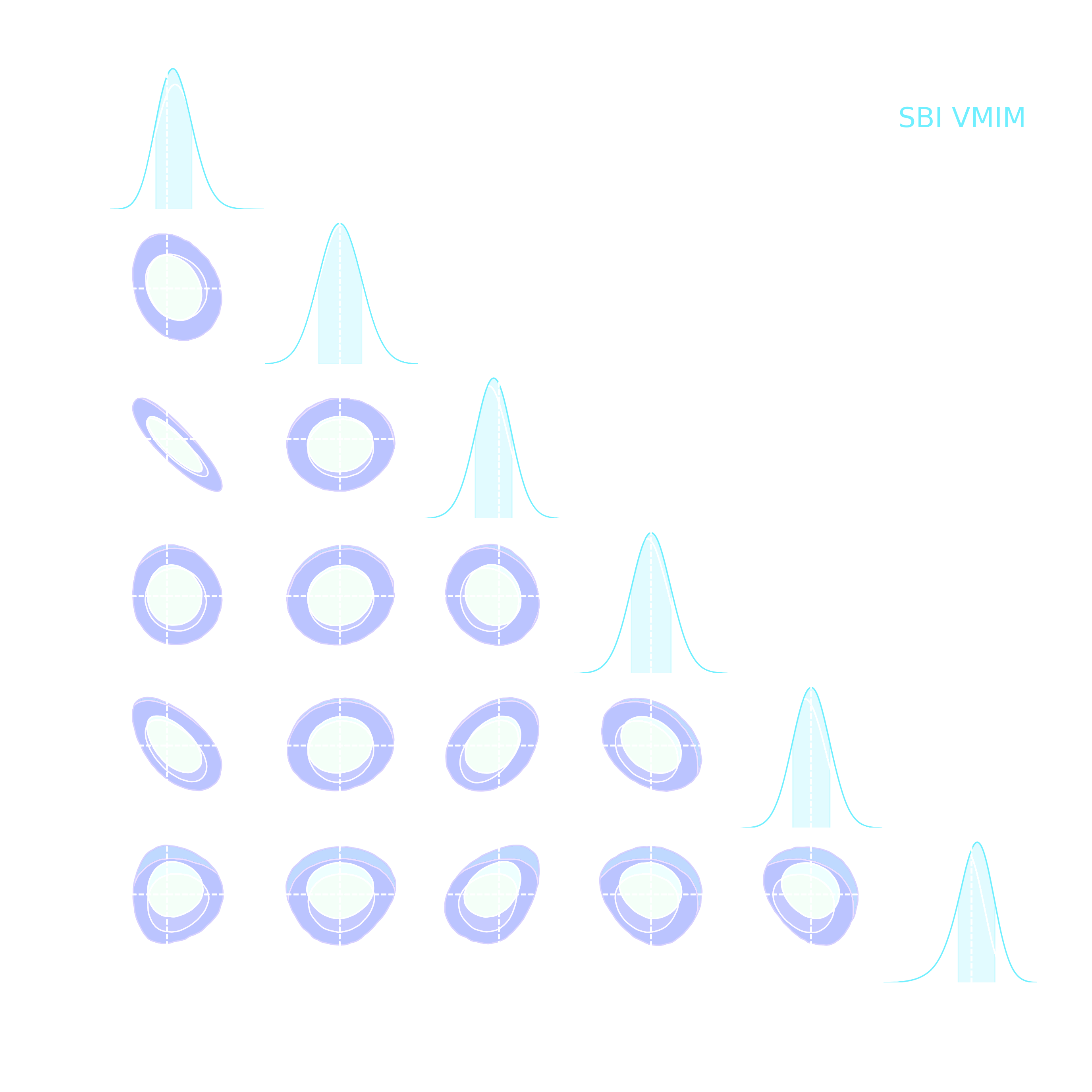
but explicit inference yields intermediate data products


simulated observed data

posterior samples $\kappa = f(z,\theta)$ with $z \sim p(z, \theta | x)$

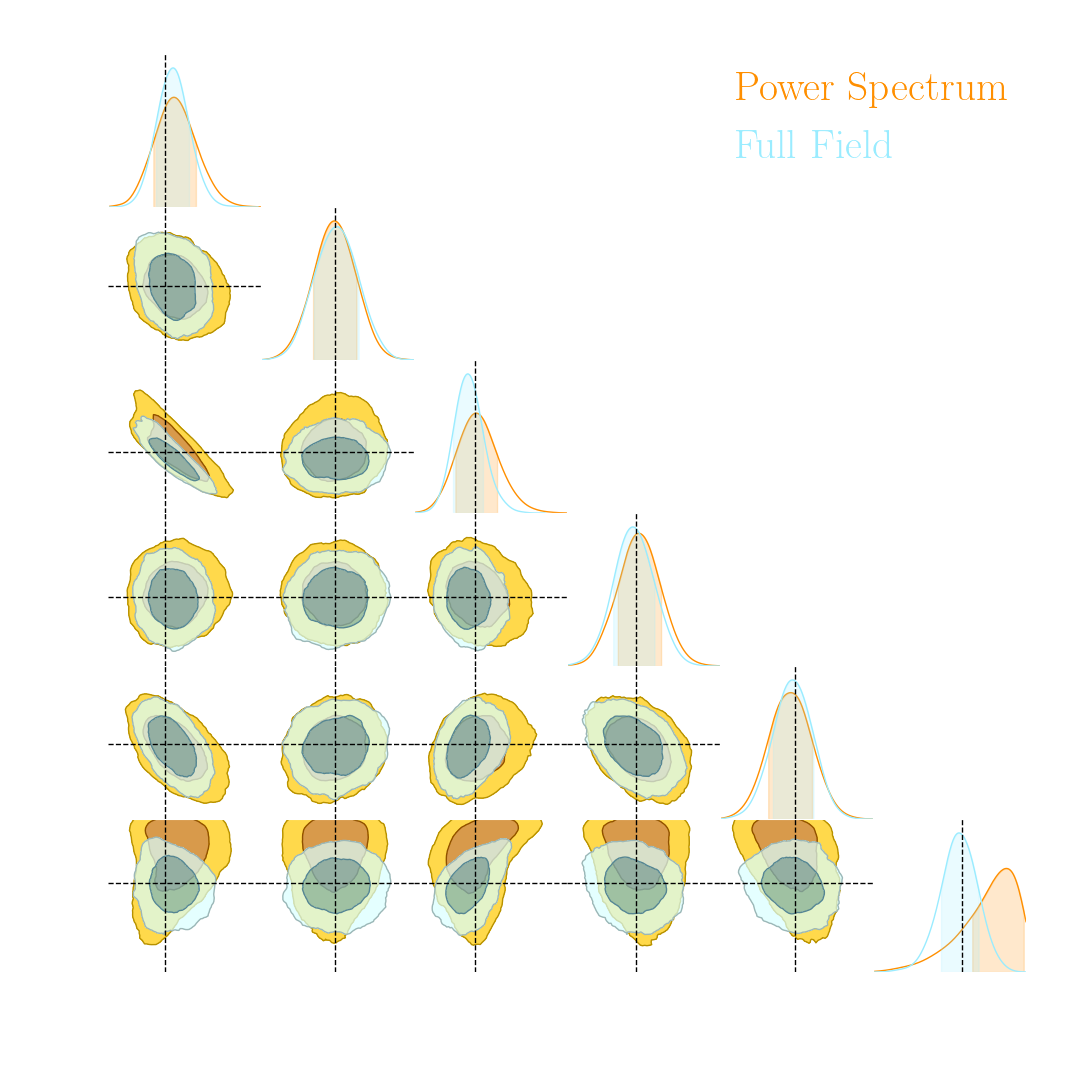
and not all neural compression techniques are equivalent


  • Most papers applying neural techniques for inference have used sub-optimal compression techniques, e.g. Mean Square Error $$ \mathcal{L} = || f_\varphi(x) - \theta ||_2^2 $$ $\Longrightarrow$ This is ok, contours will simply be larger than they could be.


  • A lot of papers are still relying on assuming a proxy Gaussian likelihoods, i.e. estimating a mean and covariance from simulations.
    $\Longrightarrow$ This is dangerous, can lead to biased contours.

Explicit Inference

Where the JAX things are

Simulators as Hierarchical Bayesian Models

  • If we have access to all latent variables $z$ of the simulator, then the joint log likelihood $p(x | z, \theta)$ is explicit.

  • We need to infer the joint posterior $p(\theta, z | x)$ before marginalization to yield $p(\theta | x) = \int p(\theta, z | x) dz$.
    $\Longrightarrow$ Extremely difficult problem as $z$ is typically very high-dimensional.

  • Necessitates inference strategies with access to gradients of the likelihood. $$\frac{d \log p(x | z, \theta)}{d \theta} \quad ; \quad \frac{d \log p(x | z, \theta)}{d z} $$ For instance: Maximum A Posterior estimation, Hamiltonian Monte-Carlo, Variational Inference.

$\Longrightarrow$ The only hope for explicit cosmological inference is to have fully-differentiable cosmological simulations!

the hammer behind the Deep Learning revolution: Automatic Differentation

  • Automatic differentiation allows you to compute analytic derivatives of arbitraty expressions:
    If I form the expression $y = a * x + b$, it is separated in fundamental ops: $$ y = u + b \qquad u = a * x $$ then gradients can be obtained by the chain rule: $$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{ \partial u}{\partial x} = 1 \times a = a$$

  • This is a fundamental tool in Machine Learning, and autodiff frameworks include TensorFlow and PyTorch.


Enters JAX: NumPy + Autograd + GPU
  • JAX follows the NumPy api! 
    
						   import jax.numpy as np
  • Arbitrary order derivatives
  • Accelerated execution on GPU and TPU

jax-cosmo: Finally a differentiable cosmology library, and it's in JAX!

Campagne, Lanusse, Zuntz et al. (2023) 

						import jax.numpy as np
						import jax_cosmo as jc

						# Defining a Cosmology
						cosmo = jc.Planck15()

						# Define a redshift distribution with smail_nz(a, b, z0)
						nz = jc.redshift.smail_nz(1., 2., 1.)

						# Build a lensing tracer with a single redshift bin
						probe = probes.WeakLensing([nz])

						# Compute angular Cls for some ell
						ell = np.logspace(0.1,3)
						cls = angular_cl(cosmo_jax, ell, [probe])
Current main features
  • Weak Lensing and Number counts probes
  • Eisenstein & Hu (1998) power spectrum + halofit
  • Angular $C_\ell$ under Limber approximation
$\Longrightarrow$ 3x2pt DES Y1 capable

Validated against the DESC Core Cosmology Library

let's compute a Fisher matrix


$$F = - \mathbb{E}_{p(x | \theta)}[ H_\theta(\log p(x| \theta)) ] $$ 

	import jax
	import jax.numpy as np
	import jax_cosmo as jc

	# .... define probes, and load a data vector

	def gaussian_likelihood( theta ):
	  # Build the cosmology for given parameters
	  cosmo = jc.Planck15(Omega_c=theta[0], sigma8=theta[1])

	  # Compute mean and covariance
	  mu, cov = jc.angular_cl.gaussian_cl_covariance_and_mean(cosmo,
														ell, probes)
	  # returns likelihood of data under model
	  return jc.likelihood.gaussian_likelihood(data, mu, cov)

	# Fisher matrix in just one line:
	F = - jax.hessian(gaussian_likelihood)(theta)
Open In Colab


  • No derivatives were harmed by finite differences in the computation of this Fisher!
  • Only a small additional compute time compared to one forward evaluation of the model

Inference becomes fast and scalable

  • Current cosmological MCMC chains take days, and typically require access to large computer clusters.

  • Gradients of the log posterior are required for modern efficient and scalable inference techniques:
    • Variational Inference
    • Hamiltonian Monte-Carlo

  • In jax-cosmo, we can trivially obtain exact gradients: 
    
										def log_posterior( theta ):
											return gaussian_likelihood( theta ) + log_prior(theta)

										score = jax.grad(log_posterior)(theta)

  • On a DES Y1 analysis, we find convergence in 70,000 samples with vanilla HMC, 140,000 with Metropolis-Hastings

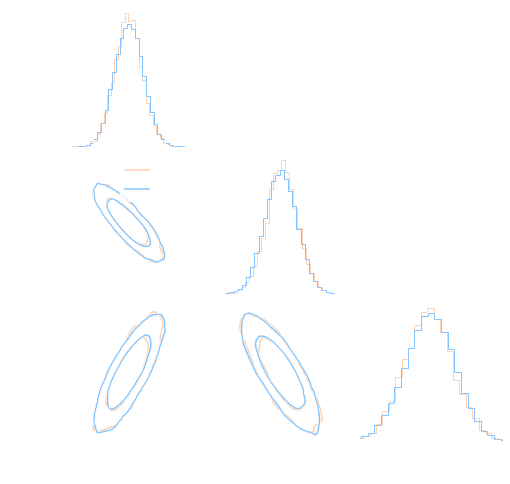
DES Y1 posterior, jax-cosmo HMC vs Cobaya MH
(credit: Joe Zuntz)

the Fast Particle-Mesh scheme for N-body simulations

The idea: approximate gravitational forces by estimating densities on a grid.
  • The numerical scheme:

    • Estimate the density of particles on a mesh
      => compute gravitational forces by FFT

    • Interpolate forces at particle positions

    • Update particle velocity and positions, and iterate

  • Fast and simple, at the cost of approximating short range interactions.
$\Longrightarrow$ Only a series of FFTs and interpolations.

introducing FlowPM: Particle-Mesh Simulations in TensorFlow

Modi, Lanusse, Seljak (2020) 

																		 import tensorflow as tf
																		 import flowpm
																		 # Defines integration steps
																		 stages = np.linspace(0.1, 1.0, 10, endpoint=True)

																		 initial_conds = flowpm.linear_field(32,       # size of the cube
																											100,       # Physical size
																											ipklin,    # Initial powerspectrum
																											batch_size=16)

																		 # Sample particles and displace them by LPT
																		 state = flowpm.lpt_init(initial_conds, a0=0.1)

																		 # Evolve particles down to z=0
																		 final_state = flowpm.nbody(state, stages, 32)

																		 # Retrieve final density field
																		 final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions),
																										final_state[0])
  • Seamless interfacing with deep learning components









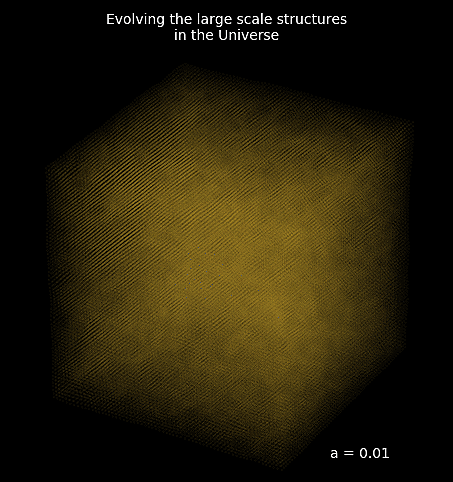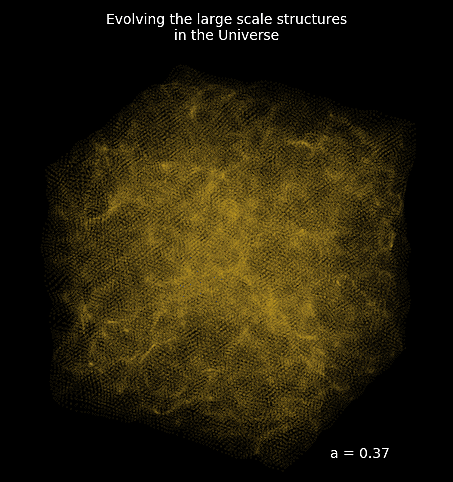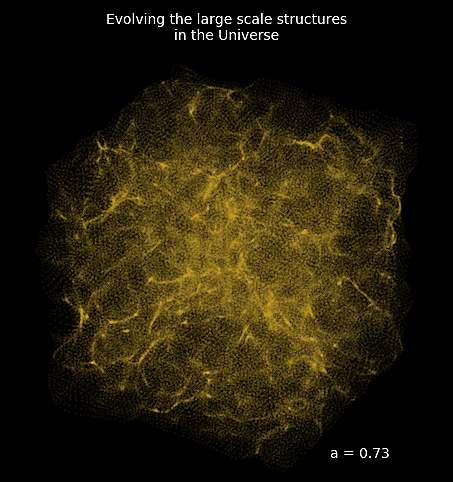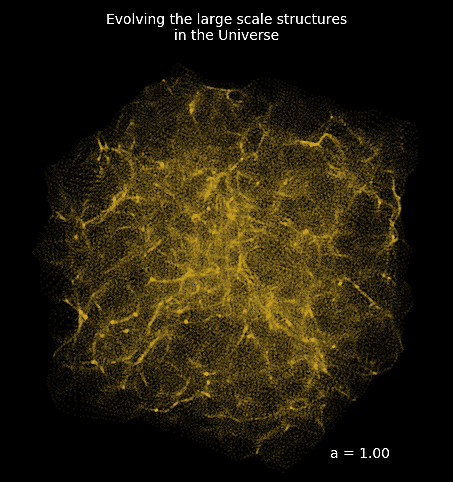
Mesh FlowPM: distributed, GPU-accelerated, and automatically differentiable simulations

  • We developed a Mesh TensorFlow implementation that can scale on GPU clusters (horovod+NCCL).

  • For a $2048^3$ simulation:
    • Distributed on 256 NVIDIA V100 GPUs

  • Don't hesitate to reach out if you have a use case for model parallelism!


  • Now developing the next generation of these tools in JAX
    • pmwd Differentiable PM library, (Li et al. 2022) arXiv:2211.09958
    • jaxdecomp: Domain Decomposition and Parallel FFTs

Hybrid physical/neural differential equations

Lanzieri, Lanusse, Starck (2022)
$$\left\{ \begin{array}{ll} \frac{d \color{#6699CC}{\mathbf{x}} }{d a} & = \frac{1}{a^3 E(a)} \color{#6699CC}{\mathbf{v}} \\ \frac{d \color{#6699CC}{\mathbf{v}}}{d a} & = \frac{1}{a^2 E(a)} F_\theta( \color{#6699CC}{\mathbf{x}} , a), \\ F_\theta( \color{#6699CC}{\mathbf{x}}, a) &= \frac{3 \Omega_m}{2} \nabla \left[ \color{#669900}{\phi_{PM}} (\color{#6699CC}{\mathbf{x}}) \right] \end{array} \right. $$
  • $\mathbf{x}$ and $\mathbf{v}$ define the position and the velocity of the particles
  • $\phi_{PM}$ is the gravitational potential in the mesh

$\to$ We can use this parametrisation to complement the physical ODE with neural networks.


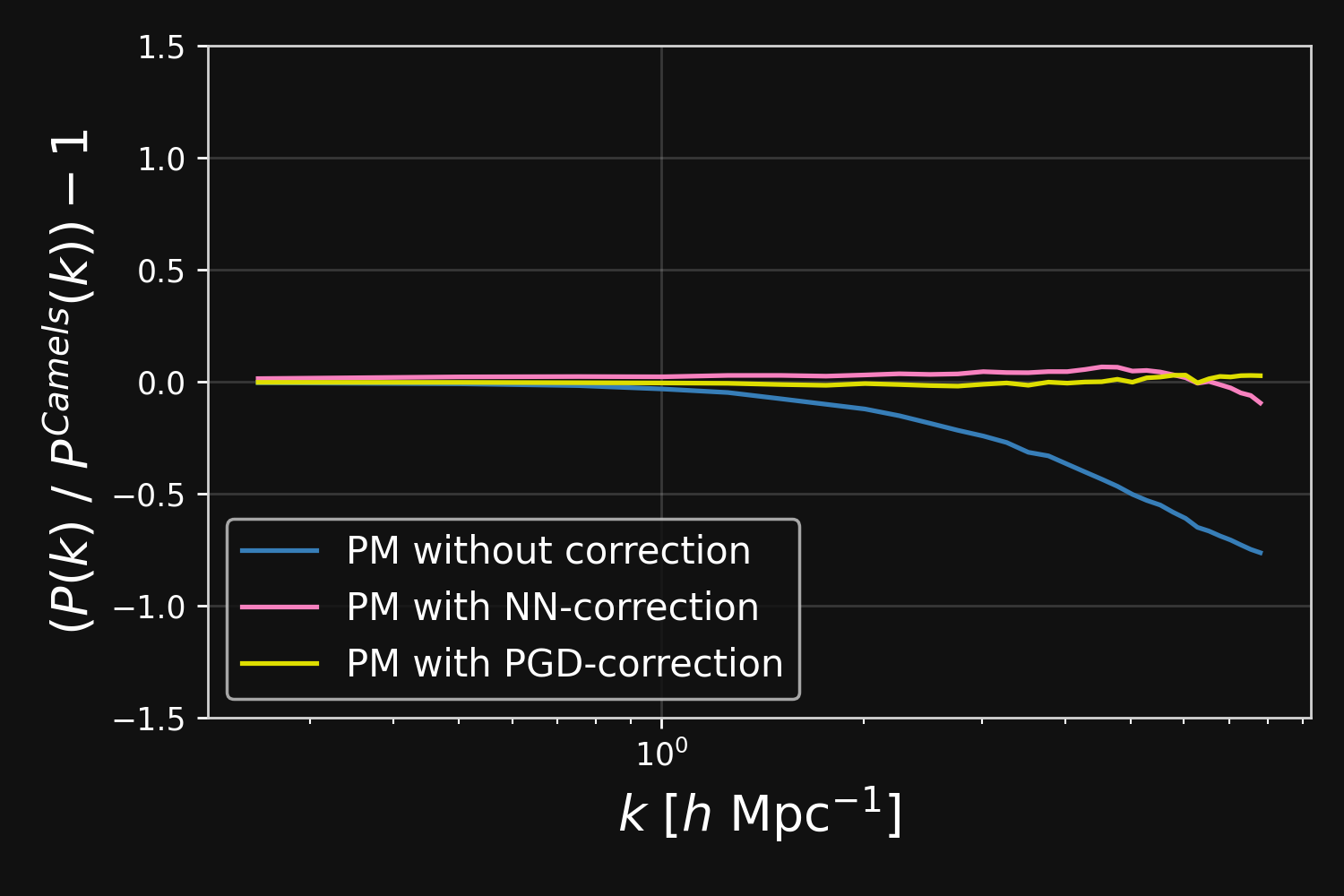
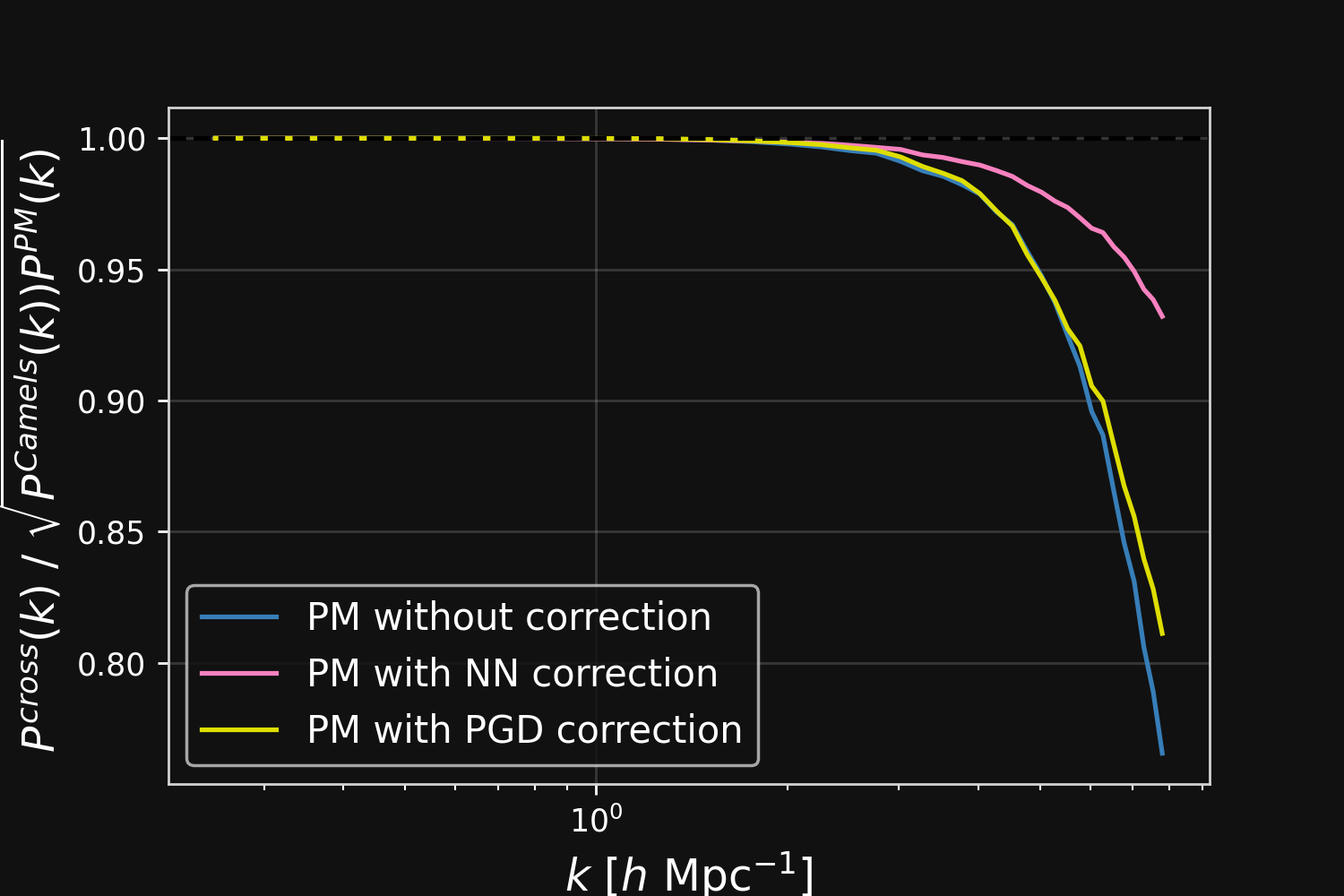
$$F_\theta(\mathbf{x}, a) = \frac{3 \Omega_m}{2} \nabla \left[ \phi_{PM} (\mathbf{x}) \ast \mathcal{F}^{-1} (1 + \color{#996699}{f_\theta(a,|\mathbf{k}|)}) \right] $$


Correction integrated as a Fourier-based isotropic filter $f_{\theta}$ $\to$ incorporates translation and rotation symmetries

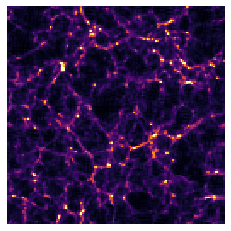
Projections of final density field



Camels simulations
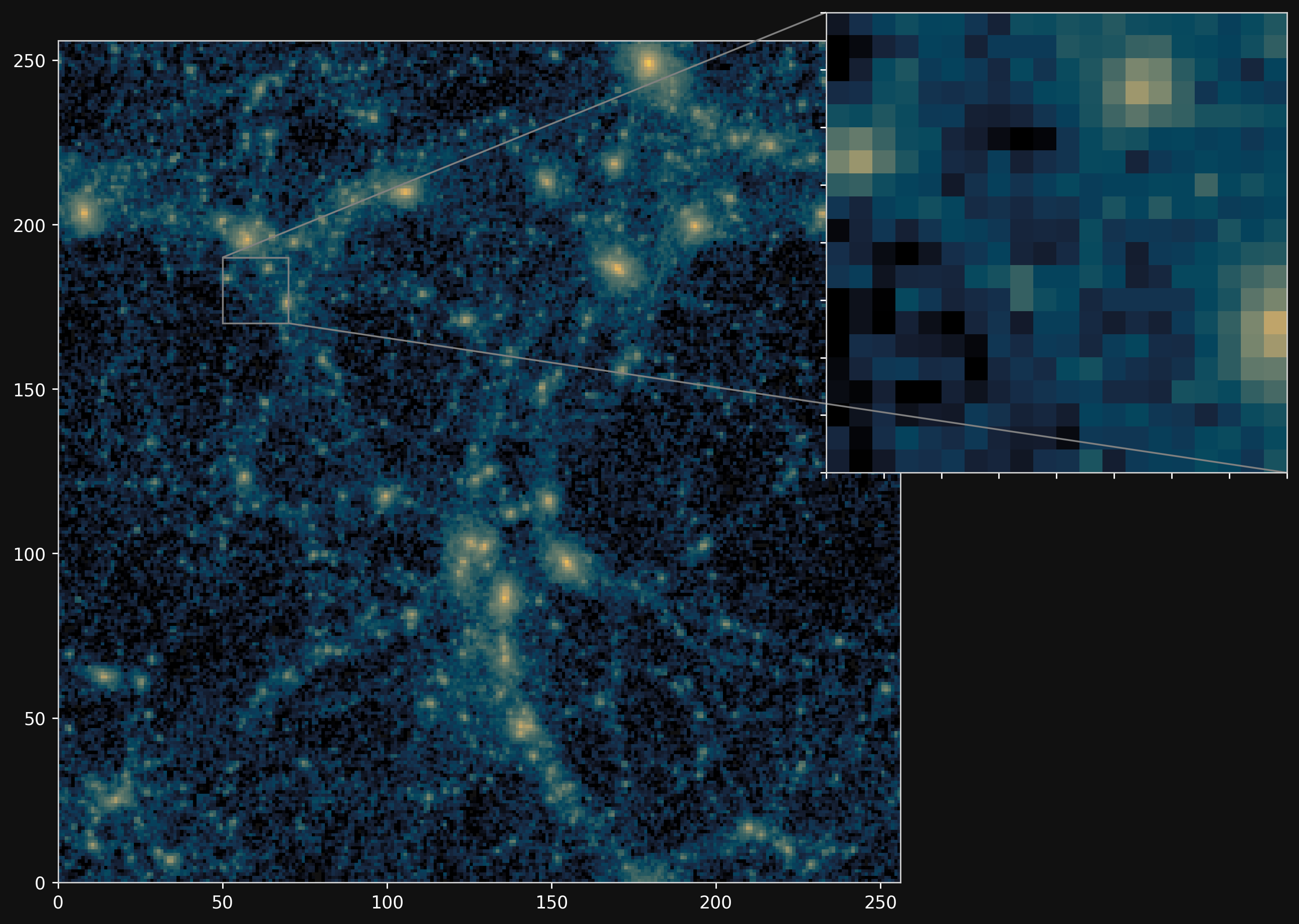
PM simulations
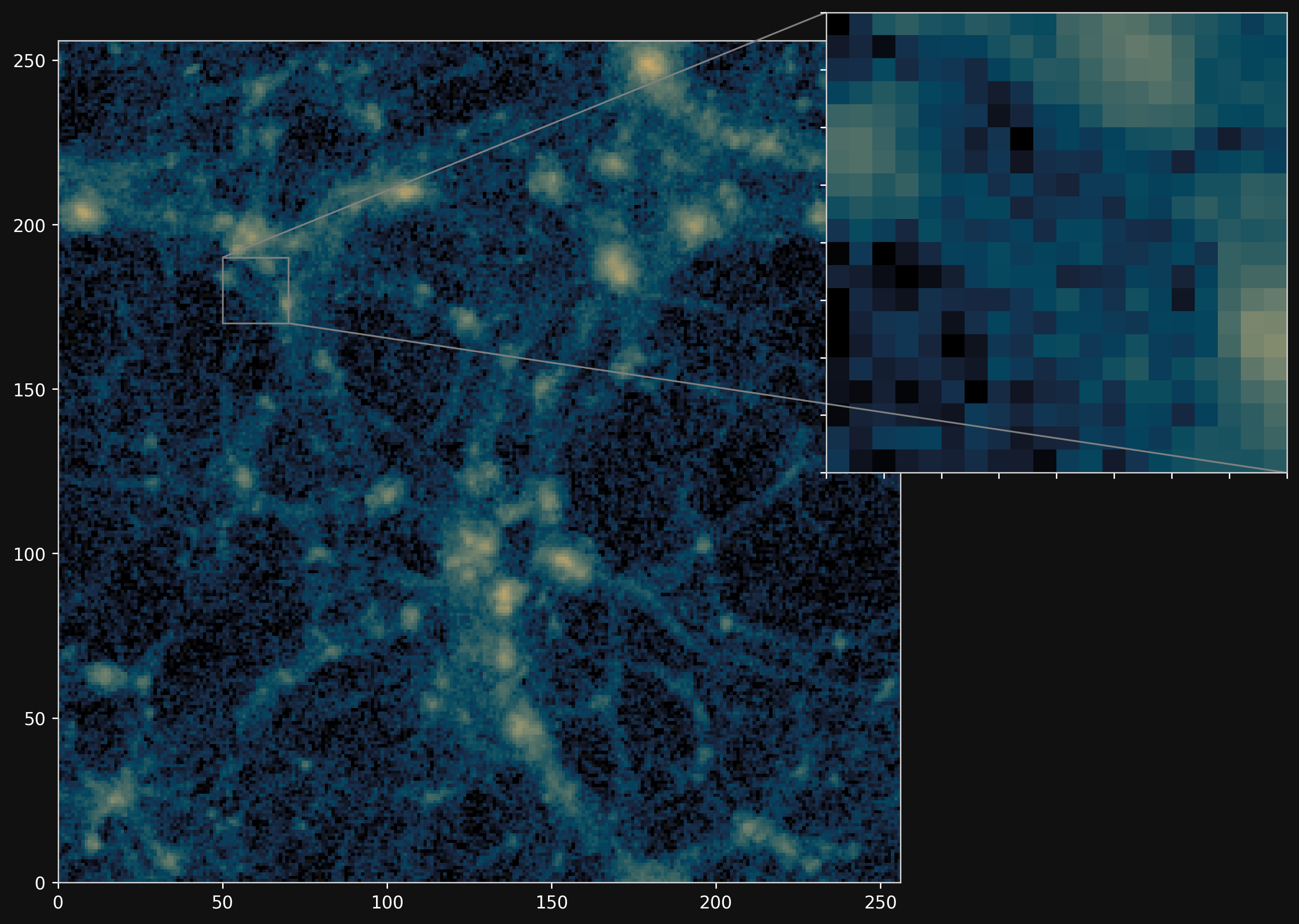
PM+NN correction

Results


  • Neural network trained using single CAMELS simulation of $25^3$ ($h^{-1}$ Mpc)$^3$ volume and $64^3$ dark matter particles at the fiducial cosmology of $\Omega_m = 0.3$


    • Forward Models in Cosmology

    Linear Field
    Final Dark Matter
    Dark Matter Halos
    Galaxies
    $\longrightarrow$
    N-body simulations
    $\longrightarrow$
    Group Finding
    algorithms
    $\longrightarrow$
    HOD models

    Differentiable sampling from Halo Occupation Distributions

    Horowitz, Hahn, Lanusse, Modi, Ferraro (2022)

    https://github.com/DifferentiableUniverseInitiative/DHOD

    • Sampling from a discrete random distribution is classically not a differentiable operation
    • Relaxed and reparameterized HOD sampling
      • Relaxed Bernoulli distributions for centrals
        $$ N_{\rm cen} = \frac{1}{1 + \exp( - (\log(\frac{p}{1 - p}) + \epsilon)/\tau) } \mbox{ with } \epsilon \sim \mathrm{Logistic}(0,1) \;. $$ where $\tau$ is a temperature parameter
      • Relaxed Binomial distribution for satelittes
        $$ N_{\rm sat} \sim \mathrm{Binomial}\left(N, p=\frac{ \left\langle N_{\rm sat}\right\rangle }{N} \right)$$

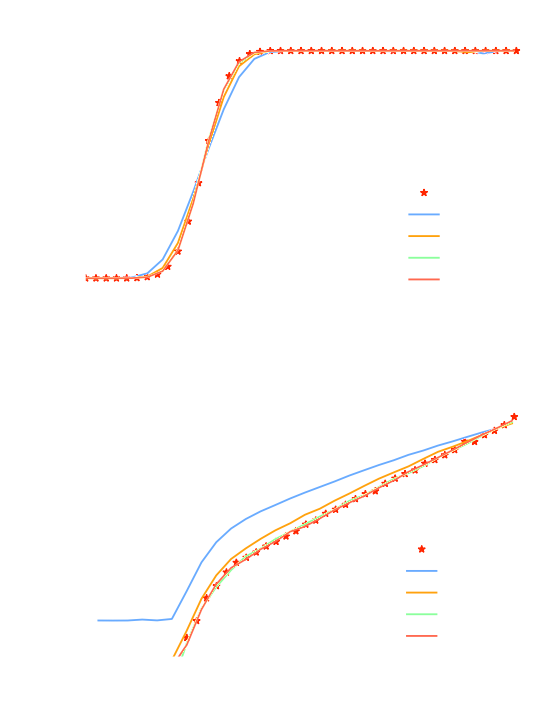
    But where are your full-field constraints with Hierarchical Bayesian Inference?

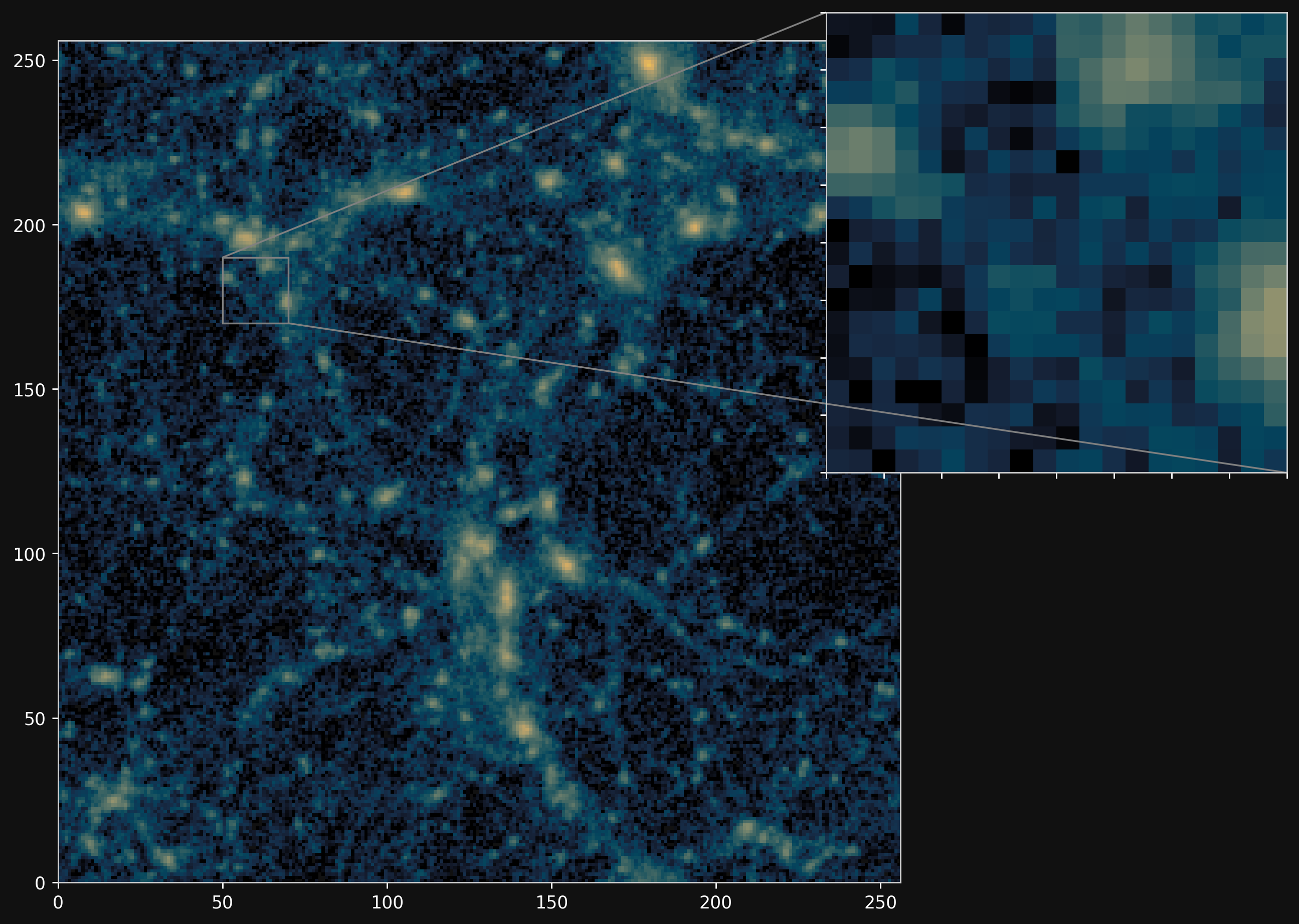
    towards reasonable resolution differentiable lensing simulations

    Lanzieri, Lanusse, et al. (2023)

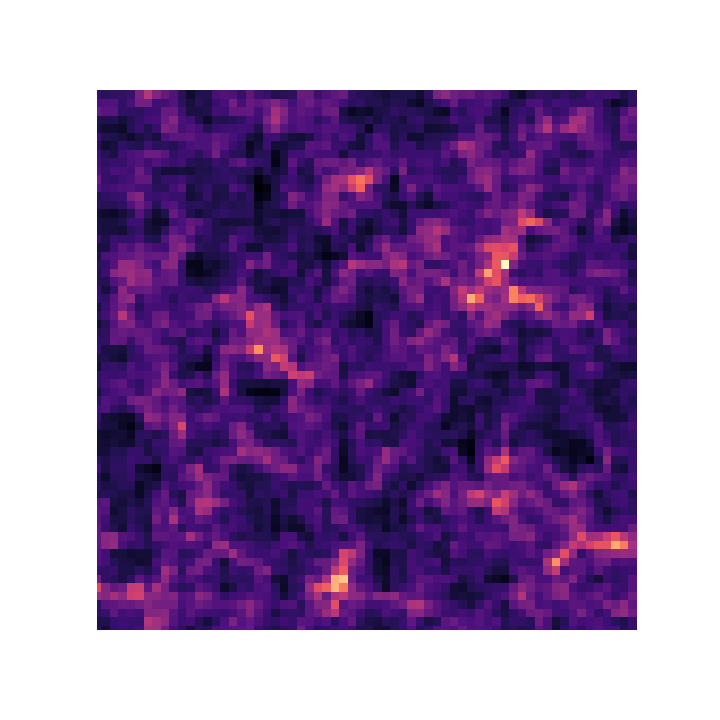
    5x5 sq deg^2 convergence field, with sources at z=0.9

    FlowPM simulation with 128^3 particles

    Conclusion

    Conclusion



    Methodology for inference over simulators
    • A change of paradigm from analytic likelihoods to simulators as physical model.

      • State of the art Machine Learning models enable Likelihood-Free Inference over black-box simulators.

      • Progress in differentiable simulators and inference methodology paves the way to full inference over probabilistic model.

    • Ultimately, promises optimal exploitation of survey data, although the "information gap" against analytic likelihoods in realistic settings remains uncertain.


    Thank you!