Implicit and Explicit Simulation-Based Inference for Cosmology
François Lanusse
slides at eiffl.github.io/talks/Paris2024
the Rubin Observatory Legacy Survey of Space and Time
- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed $\sim1000$ times
Previous generation survey: SDSS
Image credit: Peter Melchior
Current generation survey: DES
Image credit: Peter Melchior
LSST precursor survey: HSC
Image credit: Peter Melchior
We need to rethink all stages of data analysis for modern surveys
Bosch et al. 2017
Jeffrey, Lanusse, et al. 2020
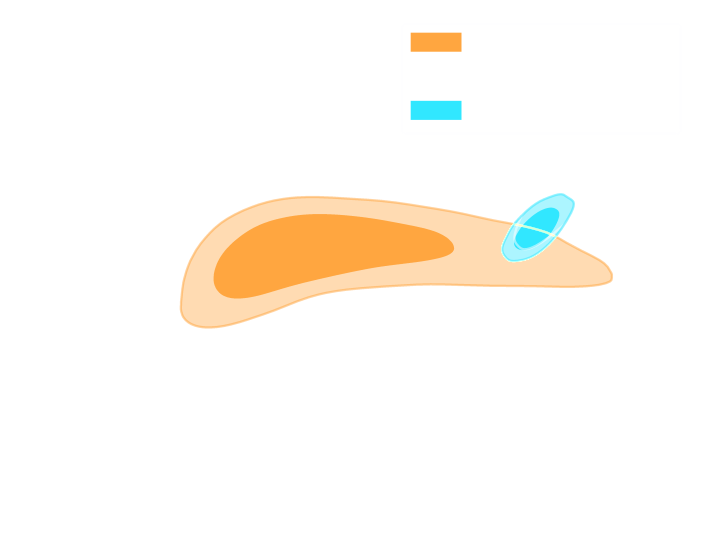
(Hikage et al. 2018)
Cheng et al. 2020
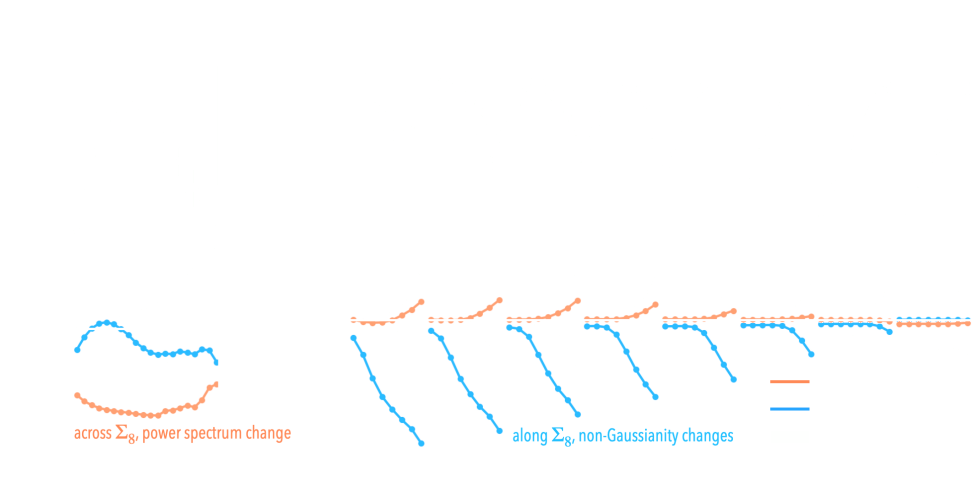
- Galaxies are no longer blobs.
- Signals are no longer Gaussian.
- Cosmological likelihoods are no longer tractable.
$\Longrightarrow$ This is the end of the analytic era...
Cosmological Simulation-Based Inference
- Instead of trying to analytically evaluate the likelihood of
sub-optimal summary statistics, let us build a forward model of the full observables.
$\Longrightarrow$ The simulator becomes the physical model. - Each component of the model is now tractable, but at the cost of a large number of latent variables.
Benefits of a forward modeling approach
- Fully exploits the information content of the data (aka "full field inference").
- Easy to incorporate systematic effects.
- Easy to combine multiple cosmological probes by joint simulations.
(Porqueres et al. 2021)
How to perform inference over forward simulation models?
- Implicit Inference: Treat the simulator as a black-box with only the ability to sample from the joint distribution
$$(x, \theta) \sim p(x, \theta)$$
a.k.a.
- Simulation-Based Inference (SBI)
- Likelihood-free inference (LFI)
- Approximate Bayesian Computation (ABC)
- Explicit Inference: Treat the simulator as a probabilistic model and perform inference over the joint posterior
$$p(\theta, z | x) \propto p(x | z, \theta) p(z, \theta) p(\theta) $$
a.k.a.
- Bayesian Hierarchical Modeling (BHM)
$\Longrightarrow$ For a given simulation model, both methods should converge to the same posterior!
Main Questions for This Talk
- Do we have the practical methodologies for both form of inference
to converge to the same solution?
- What are the tradeoffs between the two approaches?
Implicit Inference
Optimal Neural Summarisation for Full-Field Weak Lensing Cosmological Implicit Inference
Work led by:
Denise Lanzieri (now at Sony Computer Science Laboratory)
Justine Zeghal (now at University of Montreal/MILA)
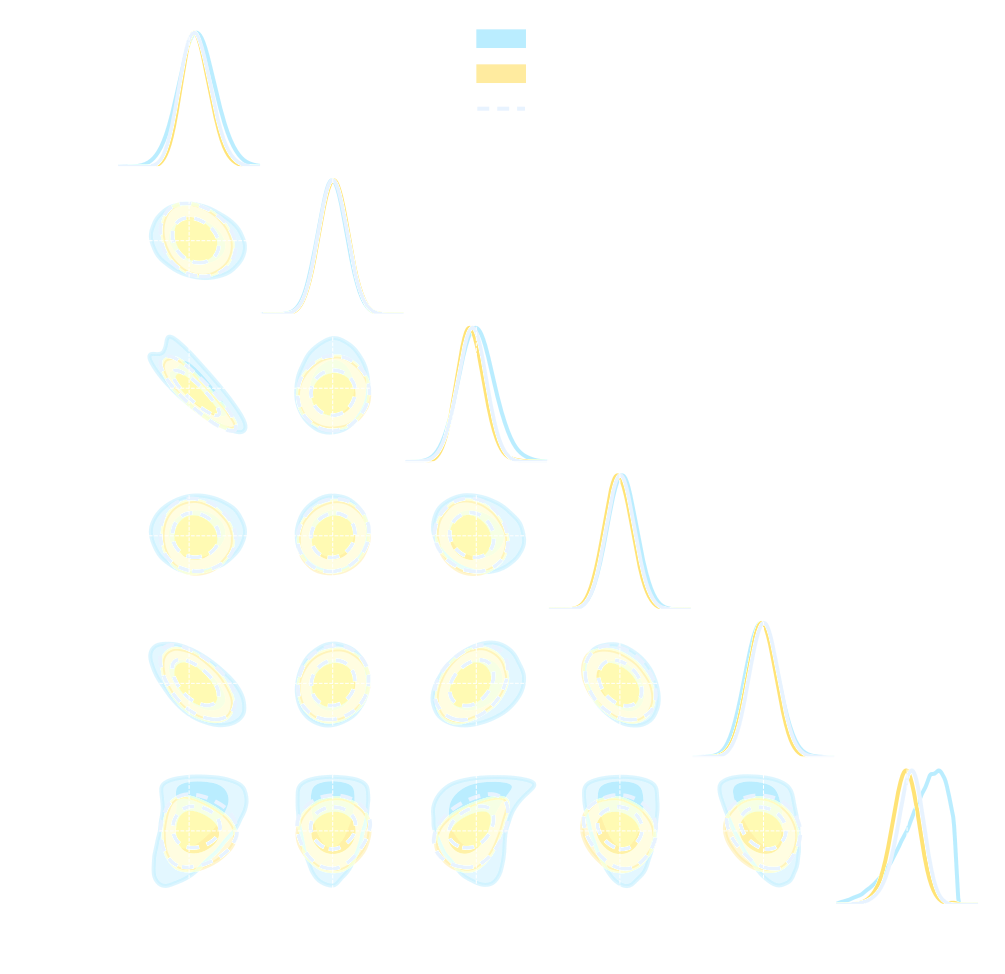
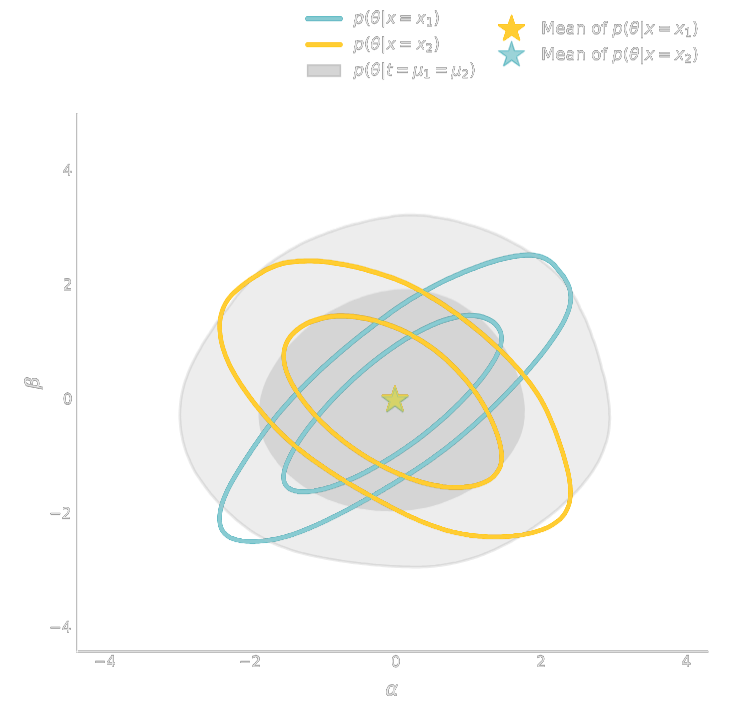
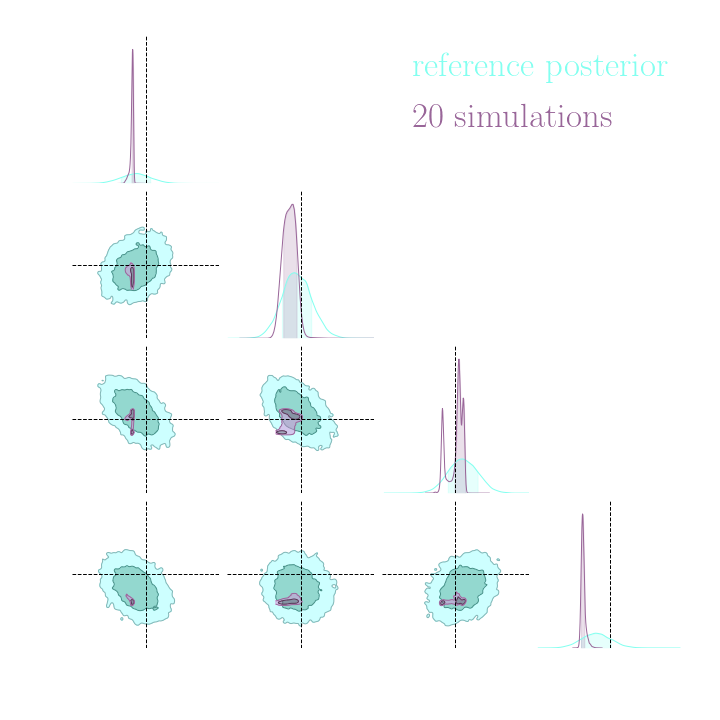
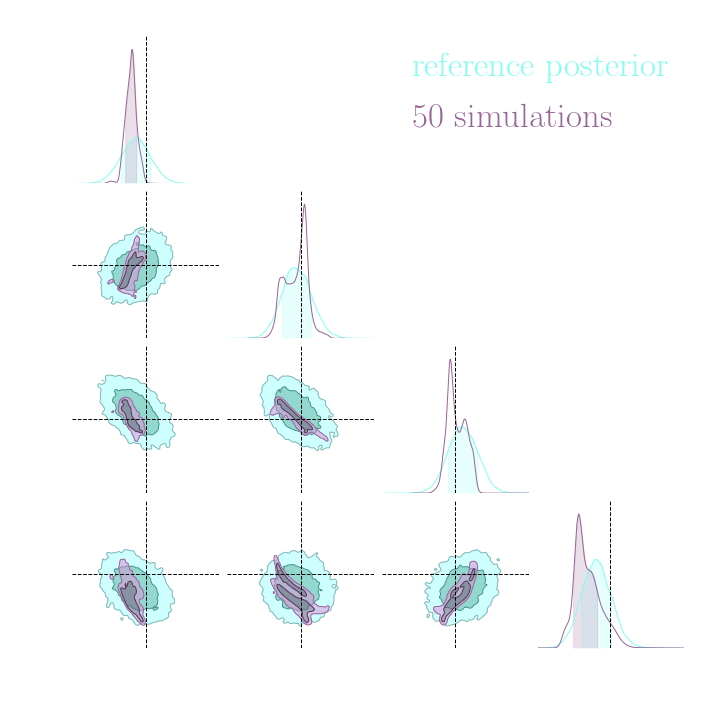
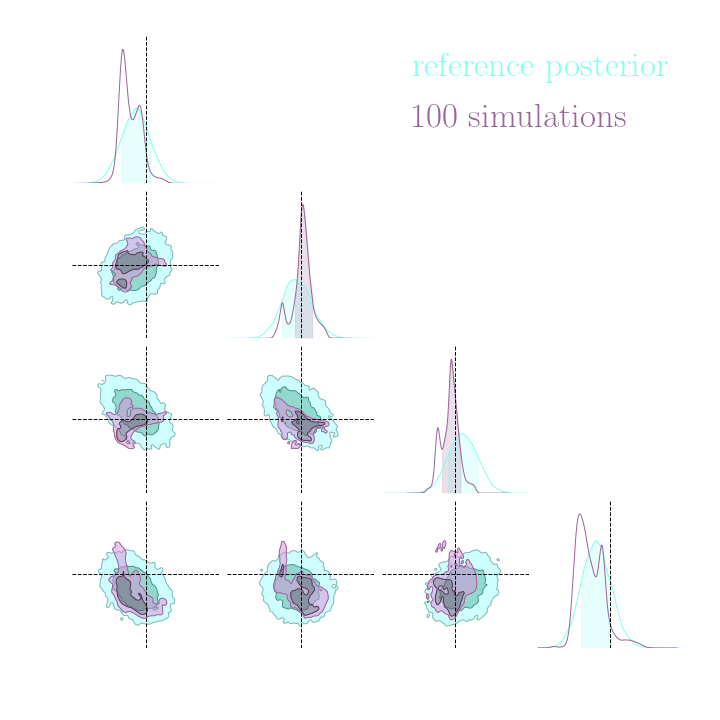
$\Longrightarrow$ Compare strategies for neural compression in setting where explicit posterior is available.
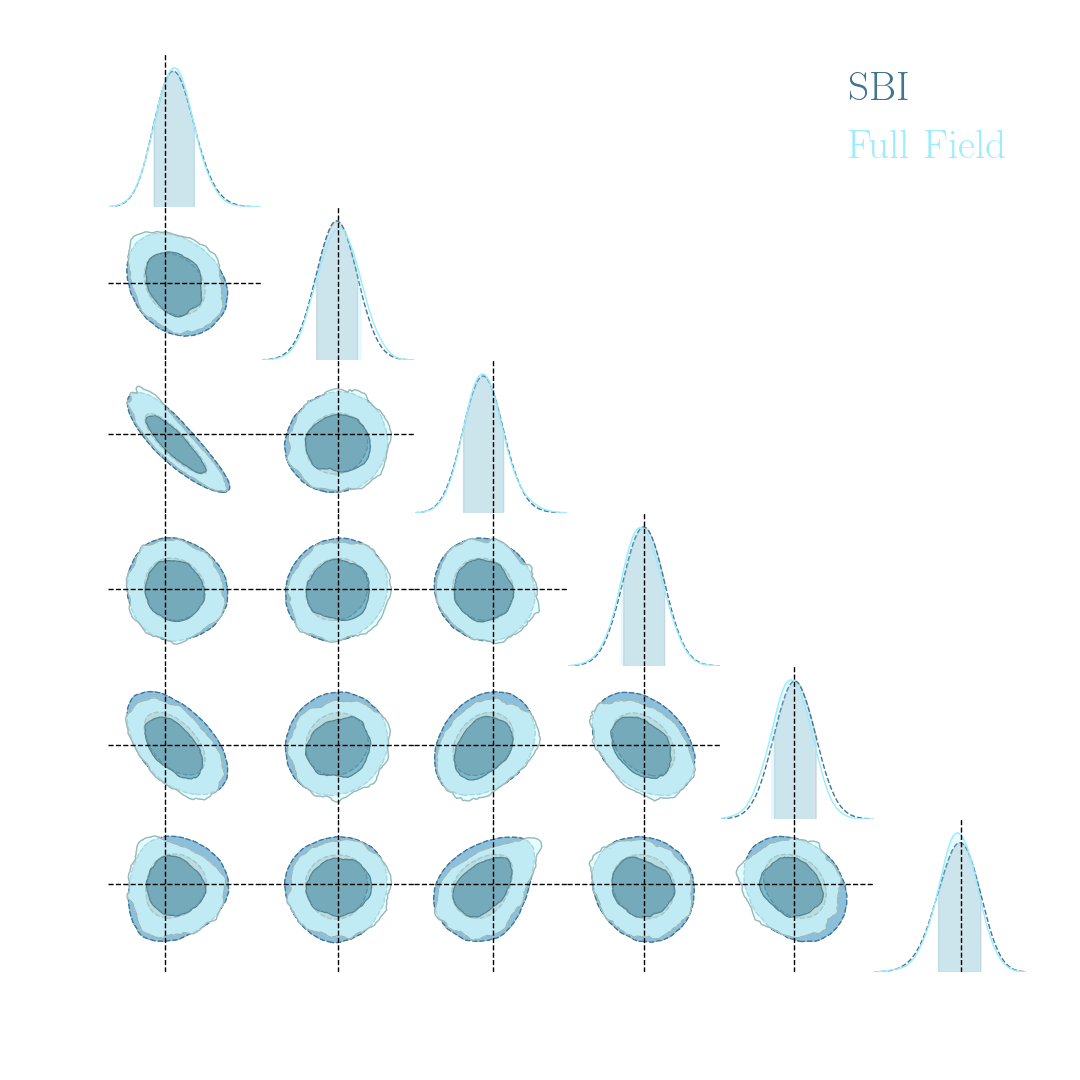
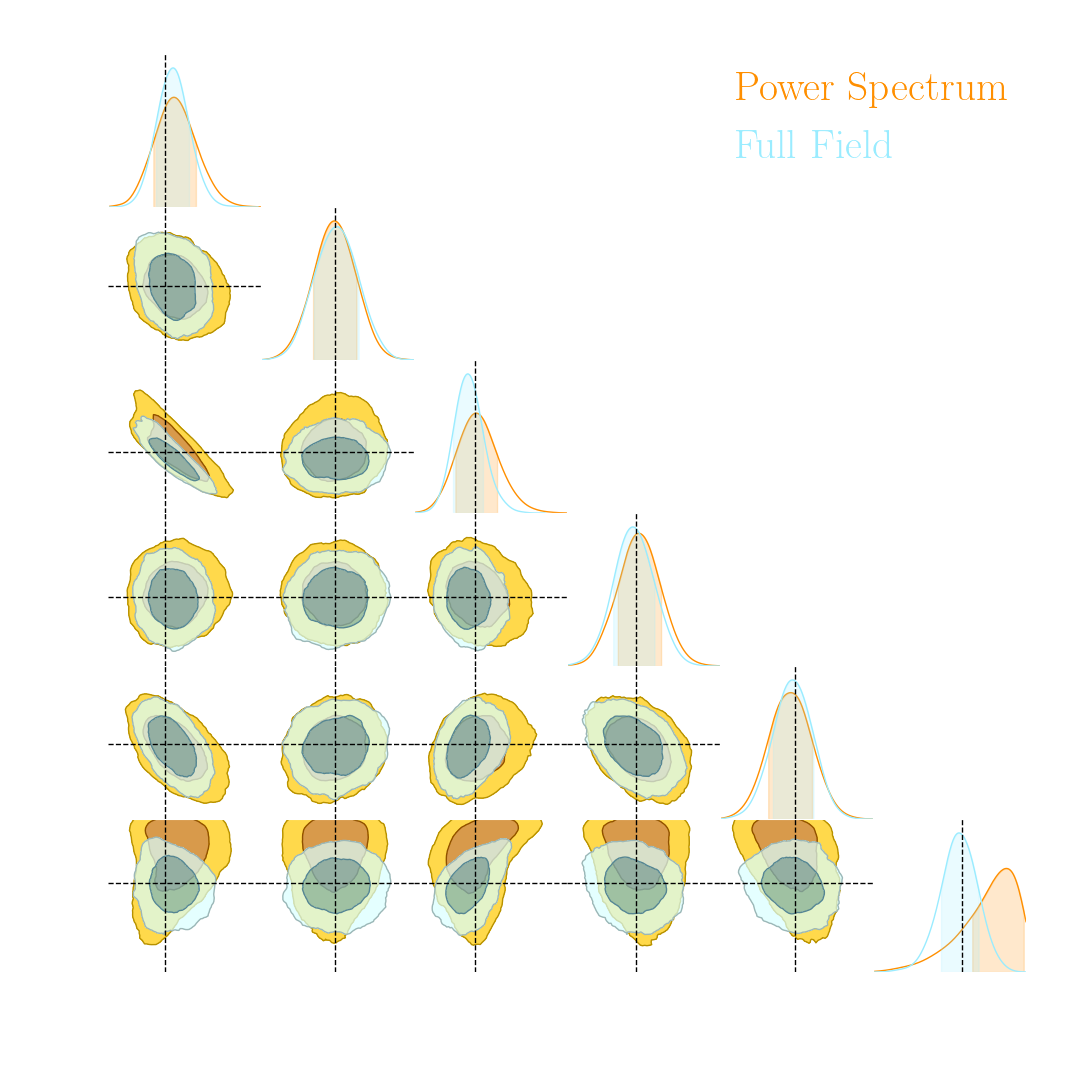
Conventional Recipe for Full-Field Implicit Inference...
A two-steps approach to Implicit Inference
- Automatically learn an optimal low-dimensional summary statistic $$y = f_\varphi(x) $$
- Use Neural Density Estimation to either:
- build an estimate $p_\phi$ of the likelihood function $p(y \ | \ \theta)$ (Neural Likelihood Estimation)
- build an estimate $p_\phi$ of the posterior distribution $p(\theta \ | \ y)$ (Neural Posterior Estimation)
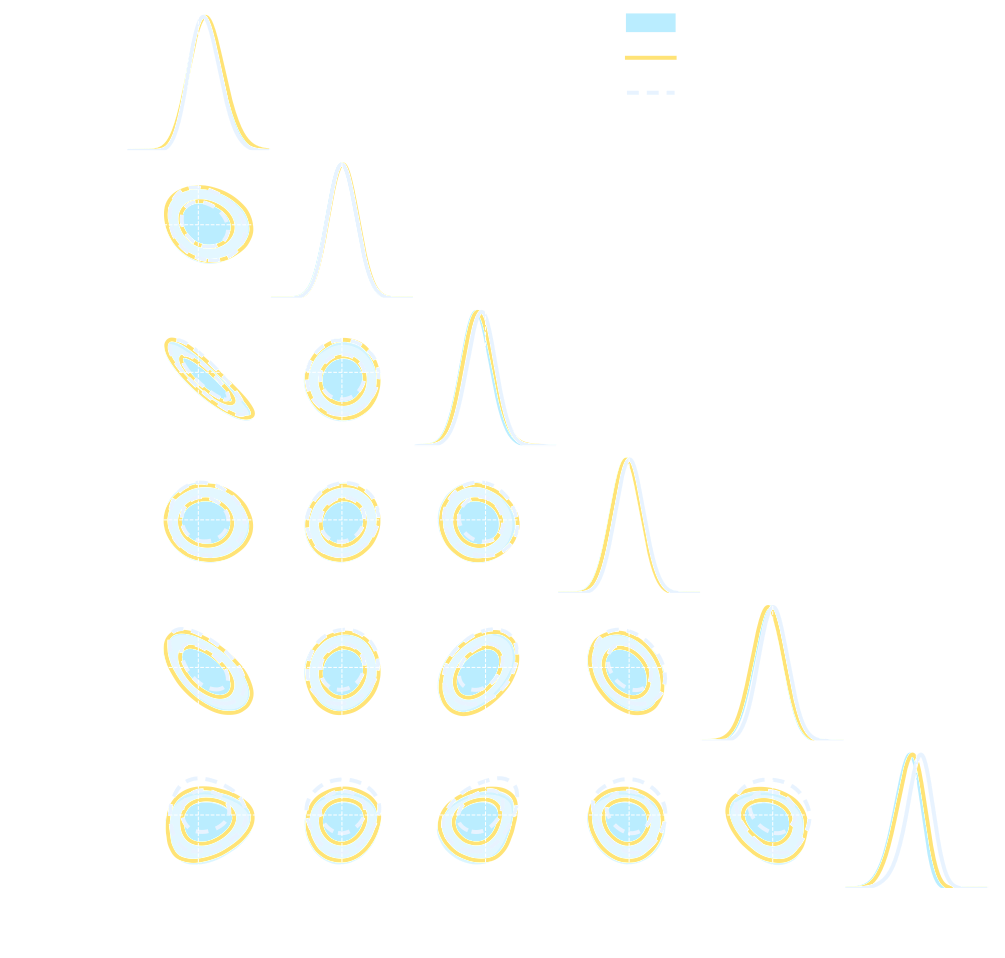
But a lot of variants!
* grey rows are papers analyzing survey data
An easy-to-use experimentation testbed: log-normal lensing simulations
DifferentiableUniverseInitiative/sbi_lens
JAX-based log-normal lensing simulation package
- 10x10 deg$^2$ maps at LSST Y10 quality, conditioning the log-normal shift parameter on $(\Omega_m, \sigma_8, w_0)$
- Provides explicit posterior by Hamiltonian-Monte Carlo (NUTS) sampling in reasonable time
- Can be used to sample a practically infinite number of maps for implicit inference
Information Point of View on Neural Summarisation
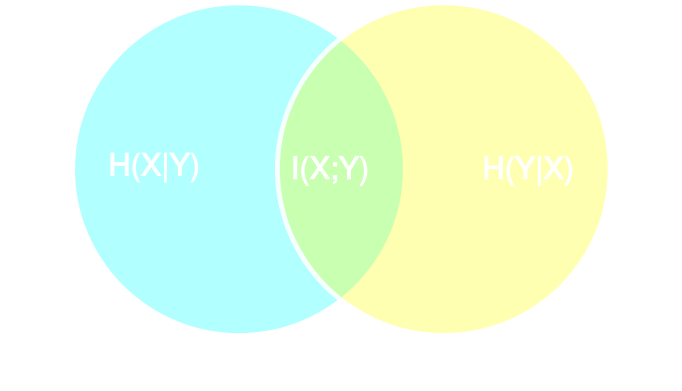
Learning Sufficient Statistics
- Summary statistics $y$ is sufficient for $\theta$ if $$ I(Y; \Theta) = I(X; \Theta) \Leftrightarrow p(\theta | x ) = p(\theta | y) $$
- Variational Mutual Information Maximization
$$ \mathcal{L} \ = \ \mathbb{E}_{x, \theta} [ \log q_\phi(\theta | y=f_\varphi(x)) ] \leq I(Y; \Theta) $$
(Barber & Agakov variational lower bound)
Jeffrey, Alsing, Lanusse (2021)
Main takeaways
- Asymptotically VMIM yields a sufficient statistics
- No reason not to use it in practice, it works well, and is asymptotically optimal
- Mean Squared Error (MSE) DOES NOT yield a sufficient statistics even asymptotically
- Same for Mean Absolute Error (MAE) and weighted versions of MSE
![]()
Accelerating Neural Density Estimation with Differentiable Simulators
Work led by:
Justine Zeghal (now at University of Montreal/MILA)
Benjamin Remy (now at Princeton)
$\Longrightarrow$ Can knowledge of gradients of the simulation model help implicit inference?
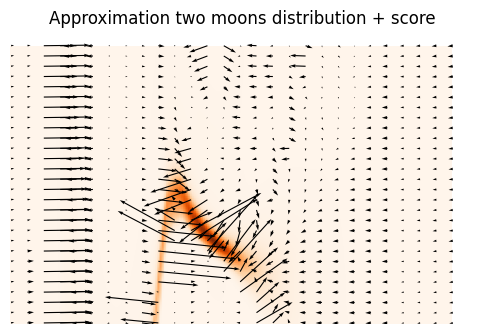
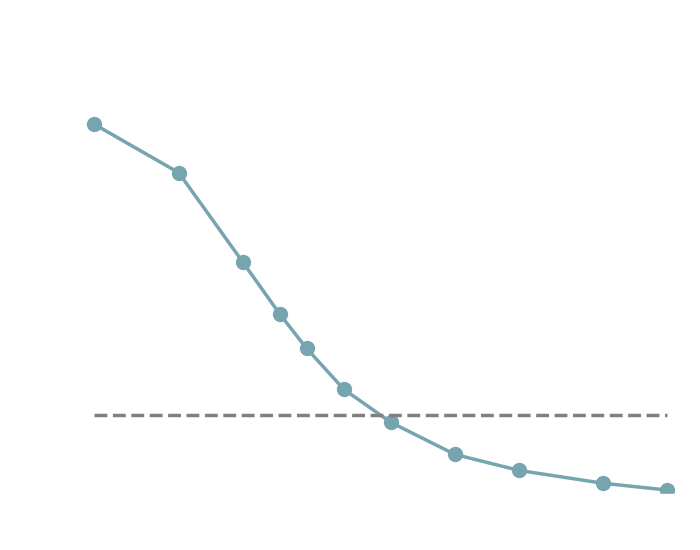
Neural Density Estimation in the low sample regime
Training a NF on two-moons by NLL with 64 samples
- It requires a lot of samples for the model to discover regularity in $\log p(x)$.
- Direct issue for Simulation Based-Inference, where the cost of each sample is high.
- Mining Gold (Brehmer et al. 2020): Having access to the score of the simulation model adds information: $$ \frac{d \log p(x)}{d x} $$
Can you train any Normalizing Flow by Score Matching?
- Let us assume an analytic distribution with known score, and train $p_\varphi(x)$ by Score Matching: $$ \mathcal{L} = \mathbb{E}_{x \sim p} \left[ \left| \nabla_x \log p(x) - \nabla_x \log p_\varphi(x) \right|^2 \right] $$
True distribution and score
Trained RealNVP and model score
Why? The score of a RealNVP with affine coupling are trivial.
$$
\left\{
\begin{array}{ll}
x_{1:d} &= z_{1:d} \\
x_{d+1:D} &= a(z_{1:d}) \times z_{d+1:D} + b(z_{1:d})
\end{array}
\right.
$$
Smooth Normalizing Flows
Adapted from Kohler et al. 2021- Key idea I: Use $\mathcal{C}^\infty$ coupling layers
$$
\left\{
\begin{array}{ll}
x_{1:d} &= z_{1:d} \\
x_{d+1:D} &= \sigma_{(a,b,c)}(z_{d+1:D})
\end{array}
\right.
$$
with $\sigma(x) := c\cdot x + \frac{1-c}{1+\exp({-\rho(x)})}$, $\rho(x) := a \cdot \left(\log\left(\frac{x}{1-x}\right) + b\right)$
and $a$, $b$, $c$ learned using a neural network.
$\Longrightarrow$ Retains non-trivial and expressive gradients. but is generally non-analytically invertible. - Key Idea II: Use a numerical inverse for $\sigma^{-1}(x)$ and implicit function theorem to compute its gradient.
$\Longrightarrow$ Computes inverse function and its gradients by solving a root-finding problem.
Illustration on two-moons
$$ \mathcal{L} = \mathbb{E}_{x \sim p} \left[ - \log p_\varphi(x) + \lambda \left| \nabla_x \log p(x) - \nabla_x \log p_\varphi(x) \right|^2 \right] $$
Training a NF on two-moons by NLL
with 64 samples
Training a NF on two-moons by combined NLL and Score Matching losses with 64 samples
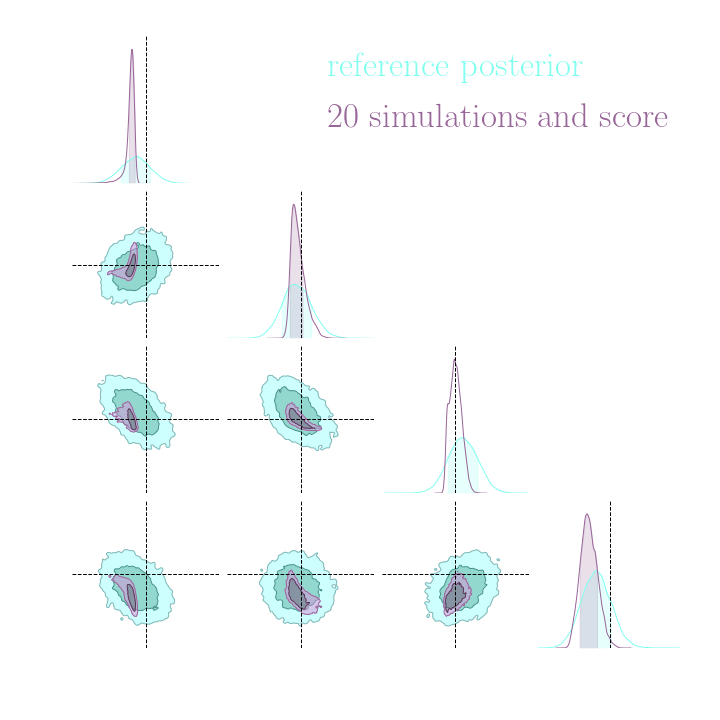
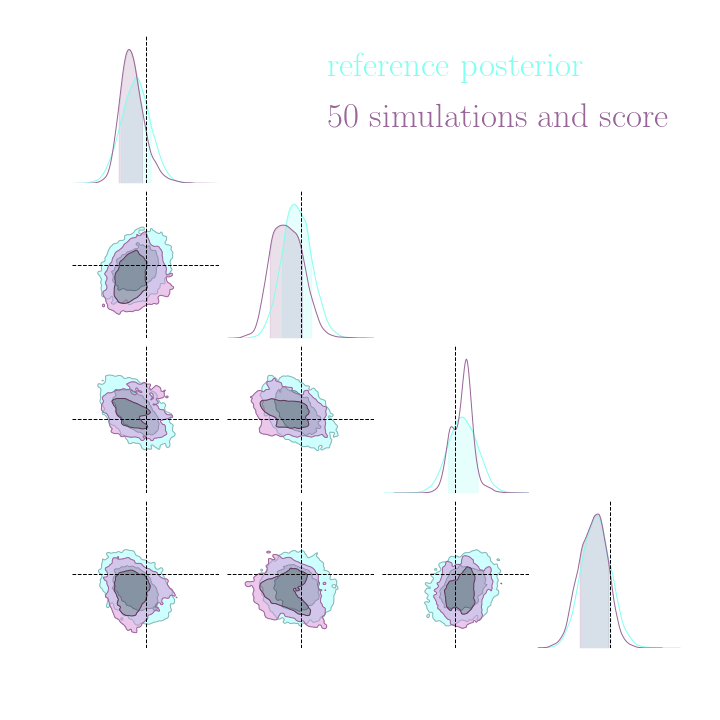
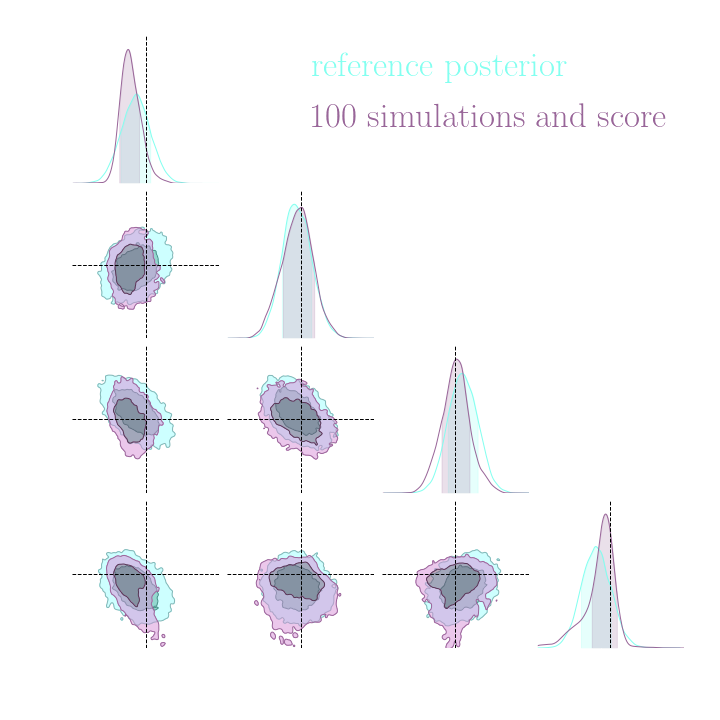
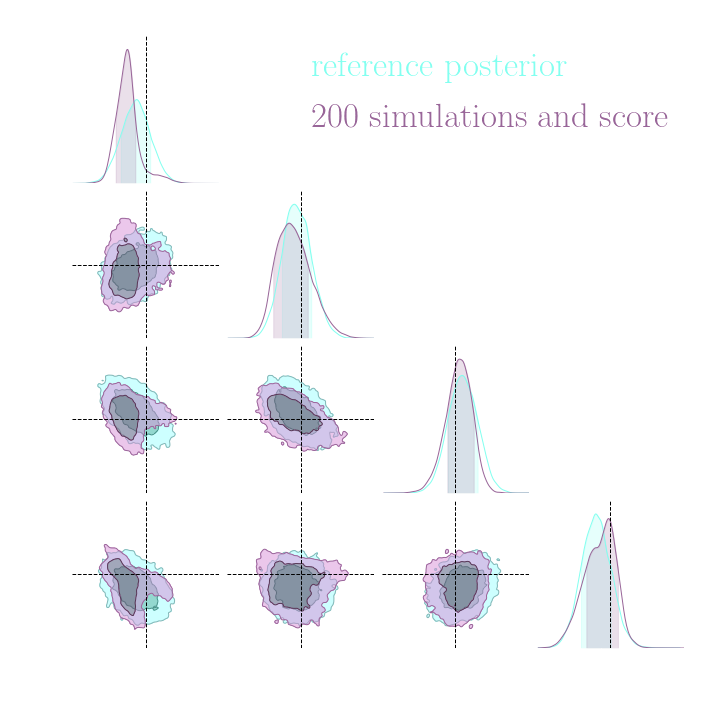
Neural Posterior Estimation with Differentiable Simulators
Zeghal, et al. (2022)
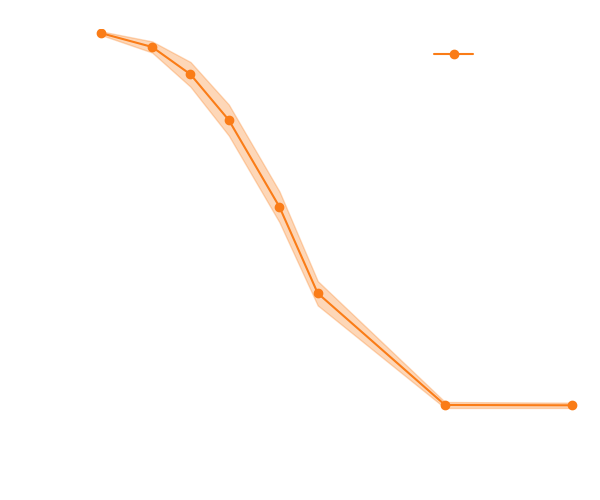
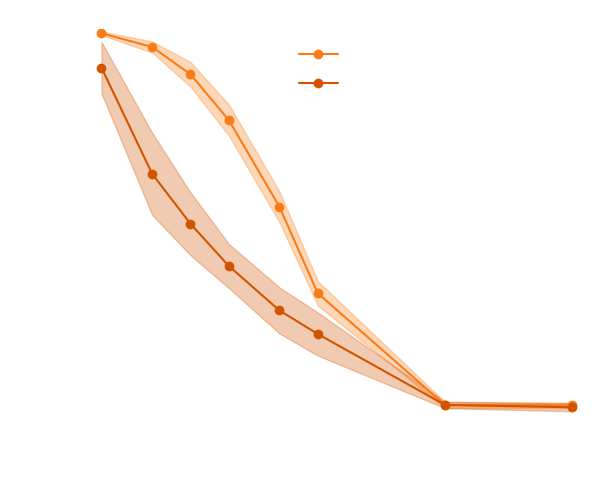
Illustration on Lotka-Volterra
With simulations only
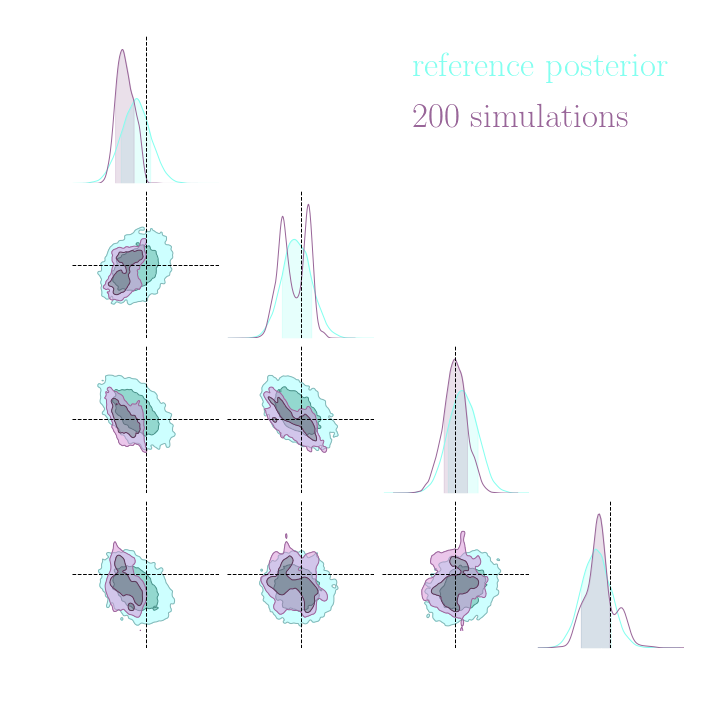
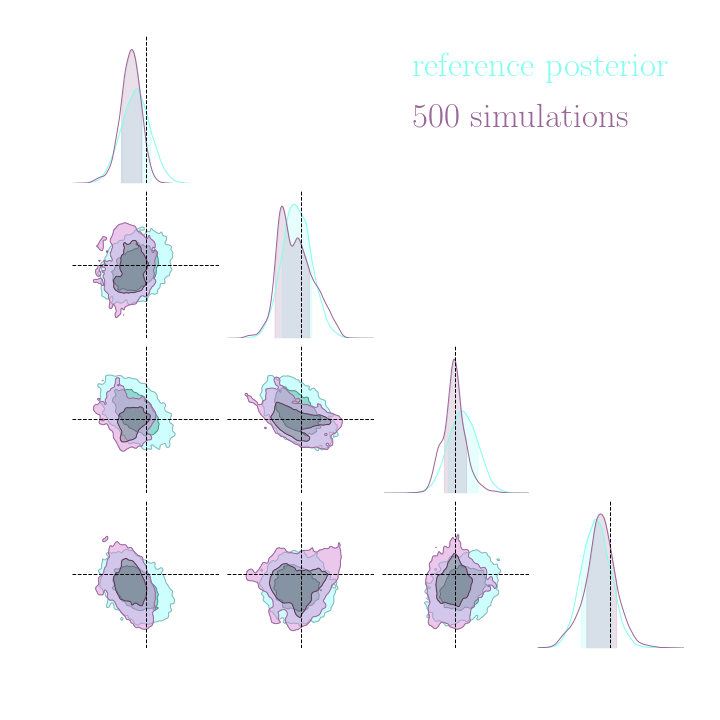
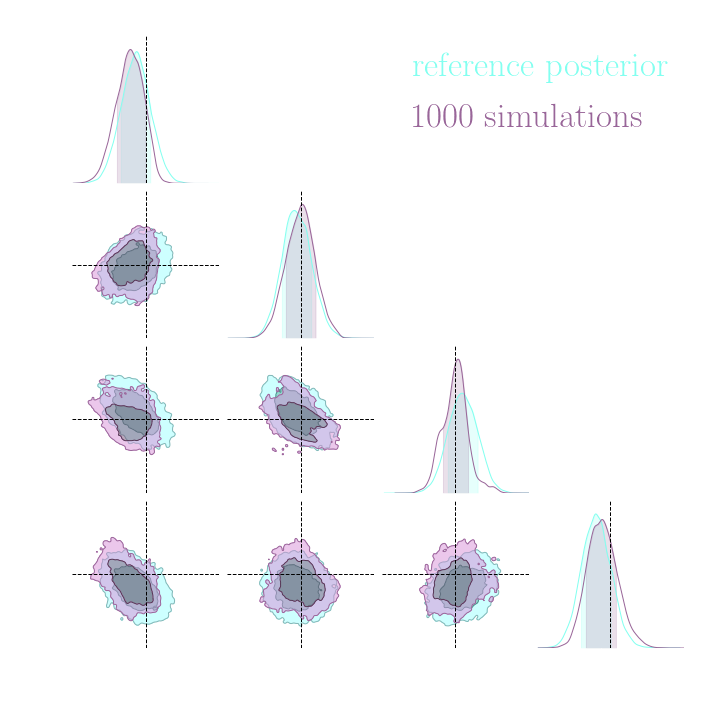
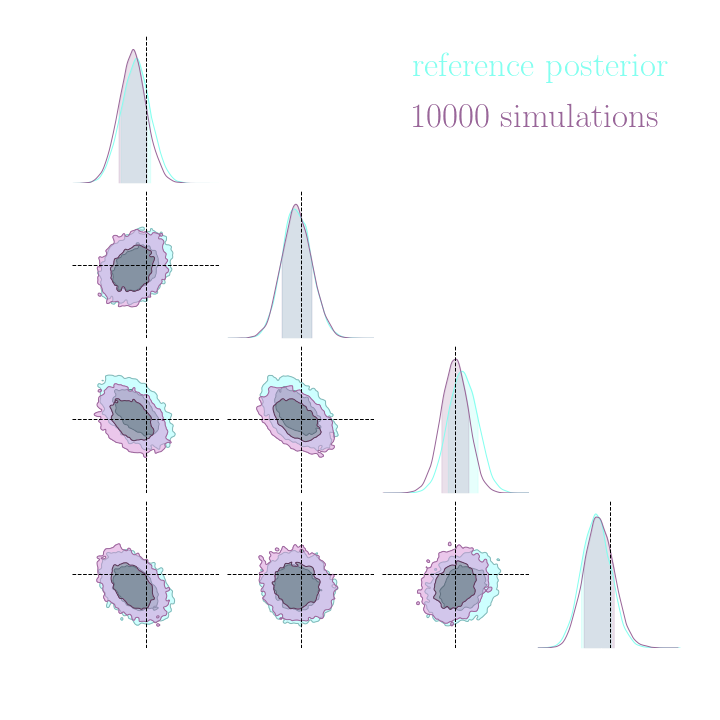
With simulations and score
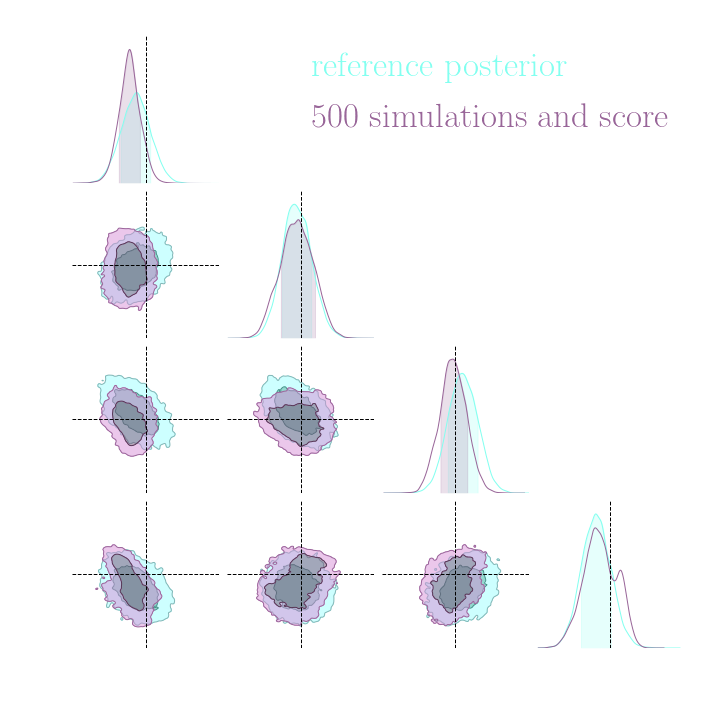
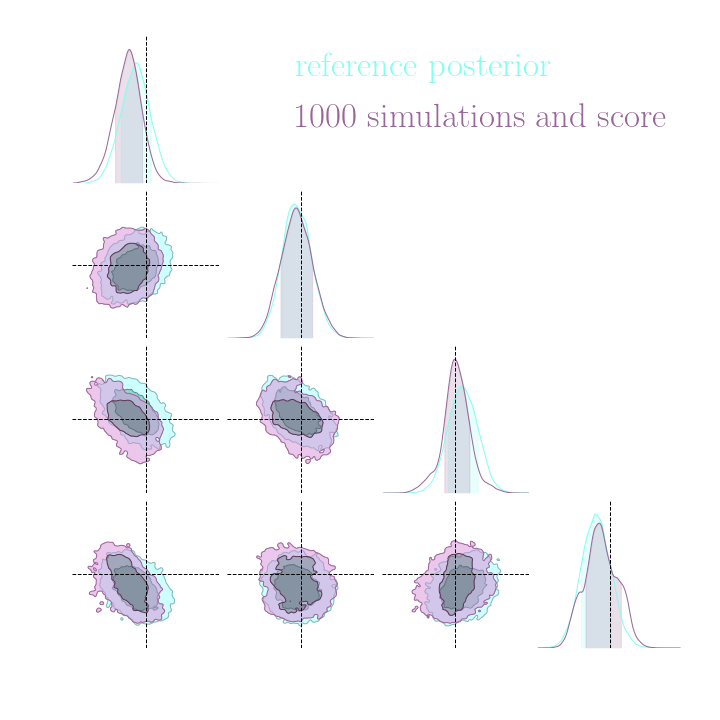
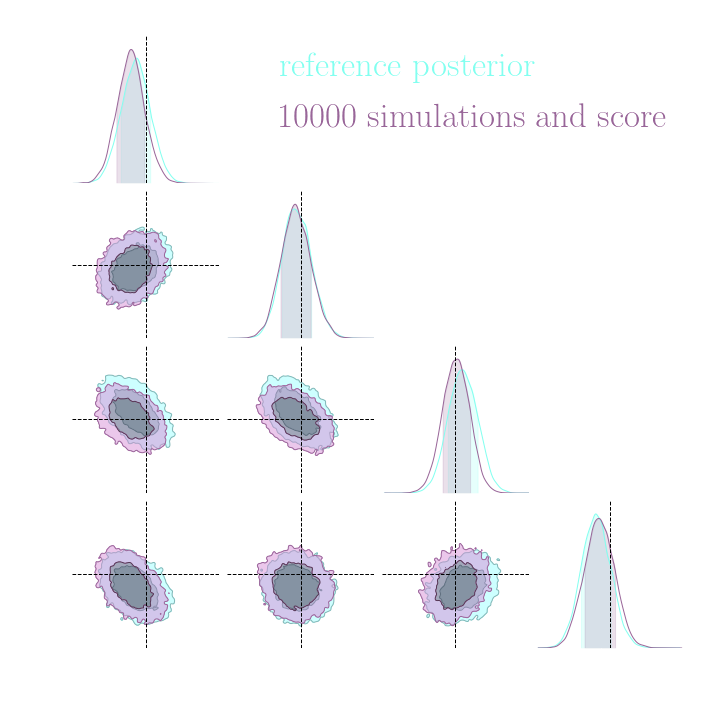
Benchmarking Inference Costs for Rubin LSST Weak Lensing Cosmology
Zeghal, Lanzieri, Lanusse, Boucaud, Louppe, et al. (2024)
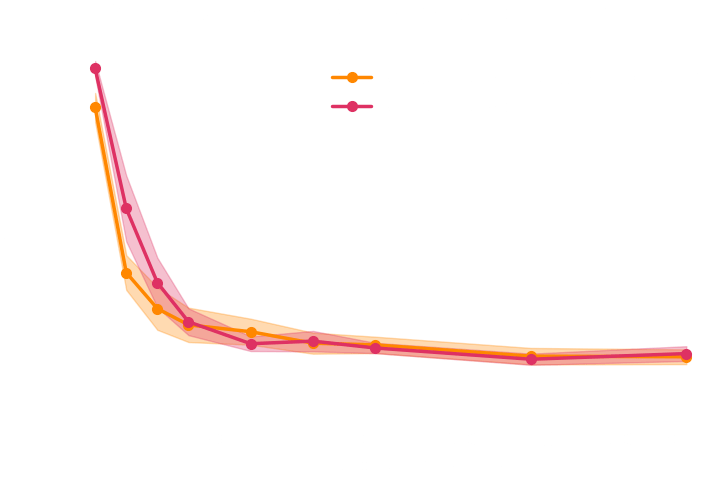
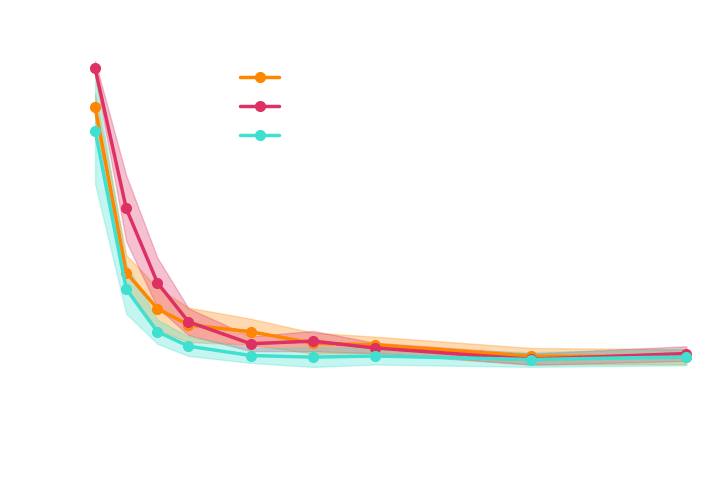
- Setting: Inference of cosmological parameters from simulated log normal weak lensing data using sbi_lens.
Main takeaways
- Gold mining can be extended to NPE with appropriate neural architectures.
- Significance of efficiency boost is problem dependent. Benefits may not be worth the added computational cost of gradient computation.
- Some good news: Even without gradients, Implicit inference is orders of magnitudes more efficient than Explicit inference.
Infusing Realistic Galaxy Properties on Large
Cosmological Simulations with SO(3) Diffusion
Work led by:
Yesukhei Jagvaral (Carnegie Mellon University)
$\Longrightarrow$ How to transfer the realism of small high resolution simulations to large cosmological volumes?
A few words about my science
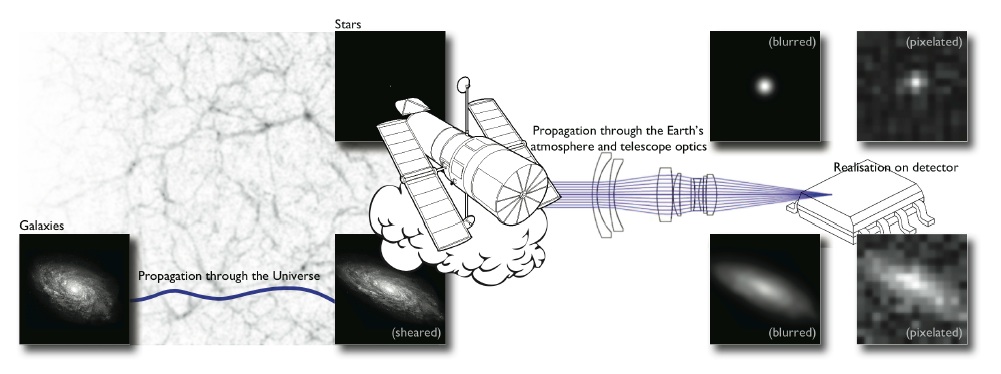
If only things were that easy...
Kiessling et al. (2015)
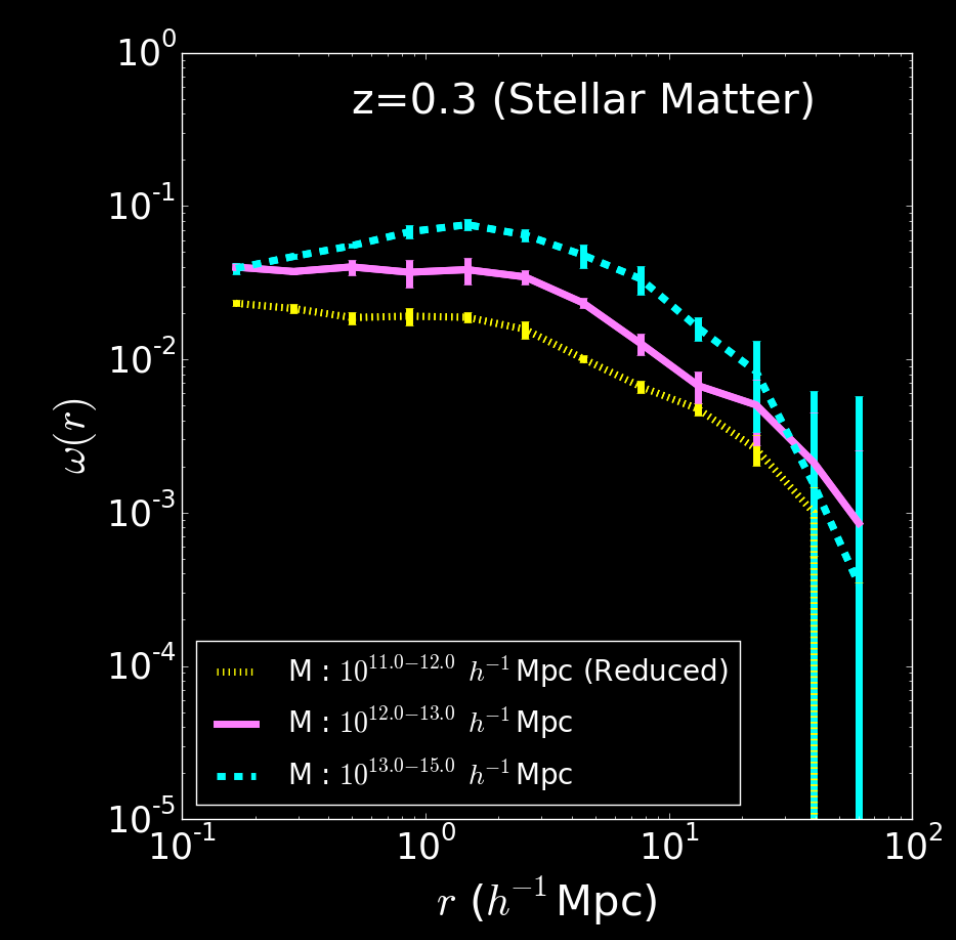
Tenneti et al. (2015)
-
Tidal interactions with local gravitational potential can lead to coherent intrinsic galaxy alignments which mimics gravitational lensing.
-
Very complicated effect in details, no single analytic model for all galaxy
types
$\Longrightarrow$ study requires expensive hydrodynamical simulations
Kiessling et al. (2015)
Our goal: inpainting galaxy orientations in affordable large scale simulations
Expensive hydrodynamical simulation
Affordable Dark Matter Only simulation
$gal \sim$ $ p( \mathbf{R} \ | \ x_{DM}, M_{DM}, \mathbf{T}_{DM}, \ldots ) \mbox{ with } \mathbf{R} \in \mathrm{SO}(3) \mathbf{} $
Let's take a step back: The 3D pose estimation problem
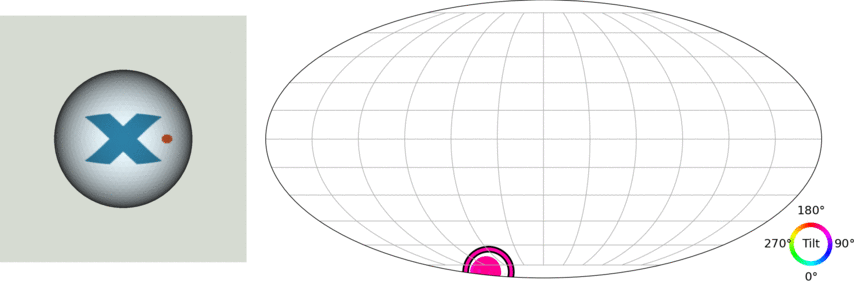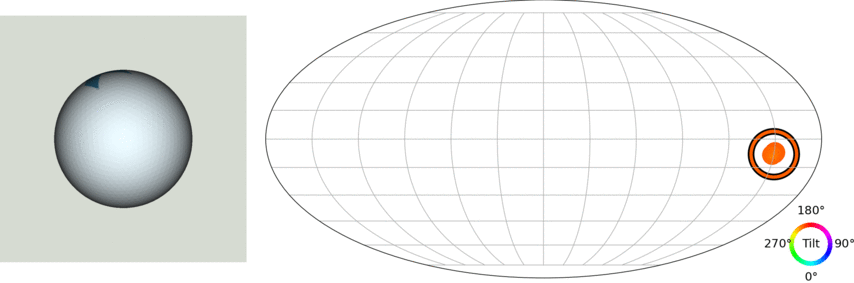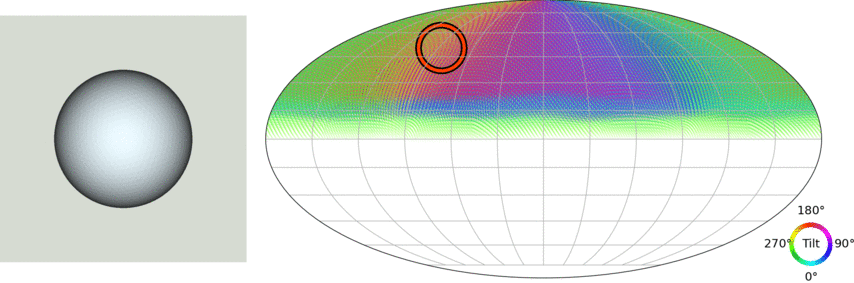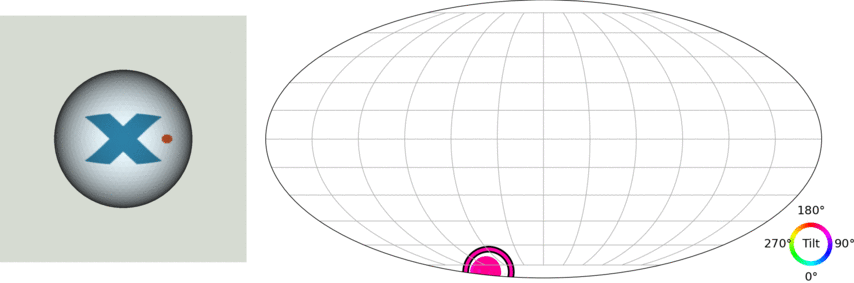
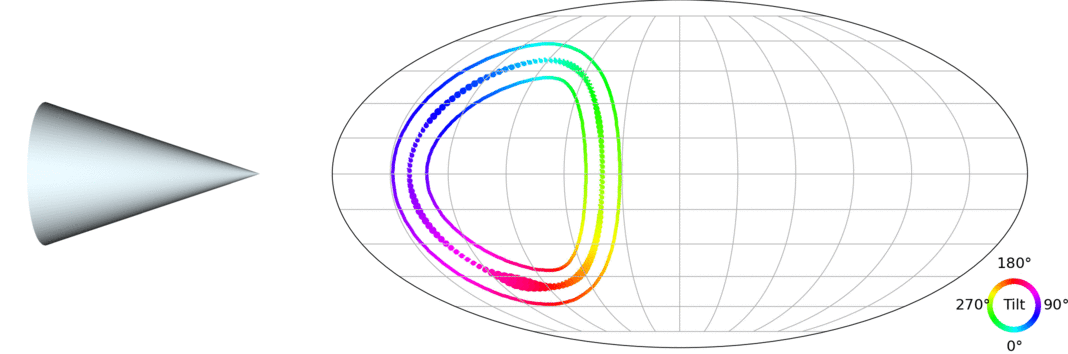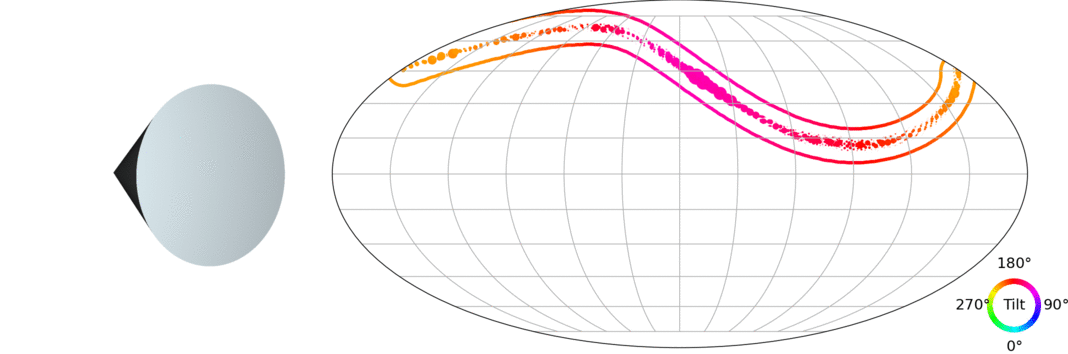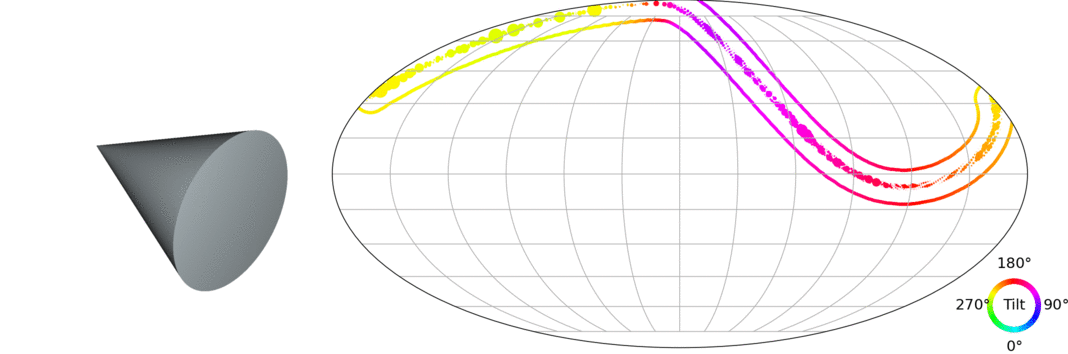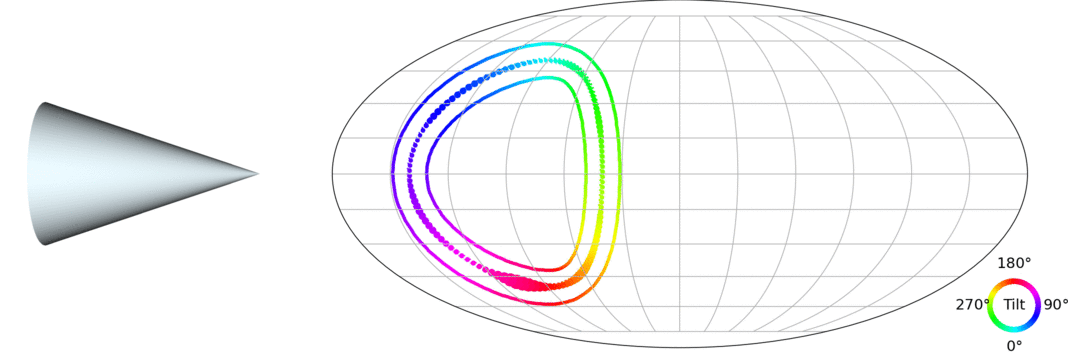
(credit: Murphi et al. 2021)
$\Longrightarrow$ We want to model a distribution $p(\mathbf{R} | y)$ where $\mathbf{R} \in \mathrm{SO}(3)$, the Lie group of 3D rotations.
Why is this not completely trivial?
- In 2024, we are very good at learning conditional distributions!
- However, 3D rotations are constrained to a non-Euclidean manifold.
- You can associate 3D rotations with the unit sphere in 4 dimensions.
How to do density estimation on SO(3) with modern tools?
What you need to know about diffusion models in $\mathbb{R}^n$
Song et al. (2021)
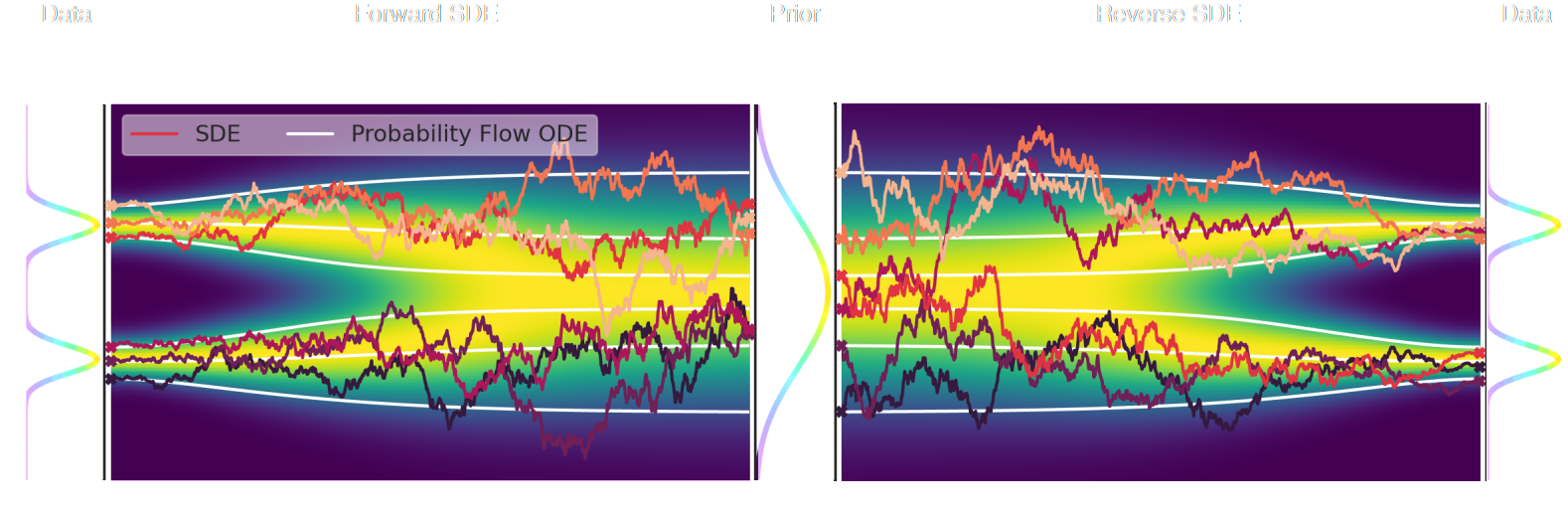
- The SDE defines a marginal distribution $p_t(x)$ as the convolution of the target distribution $p(x)$ with a noise kernel $p_{t|s}(\cdot | x_s)$: $$p_t(x) = \int p(x_s) p_{t|s}(x | x_s) d x_s$$
- For a given forward SDE that evolves $p(x)$ to $p_T(x)$, there exists a reverse SDE that evolves $p_T(x)$ back into $p(x)$. It involves having access to the marginal score $\nabla_x \log_t p(x)$.
- You can sample by solving the associated ODE (aka probability flow ODE): $\mathrm{d} \mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g(t)^2 \nabla \log p_t(\mathbf{x})] \mathrm{d} t $
Extending this framework to the $\mathrm{SO}$(3) manifold
- There are some good news: The same result of existence of reverse SDE holds.
Things we need to figure out:
- How do we define this noise process as to remain on the manifold
- How do we solve differential equations on the manifold
Going back to the heat equation
The heat kernel is the solution of the heat diffusion equation and corresponds to the
transition density of Brownian motion $p_{t | s}(\cdot | x_s)$ for $t>s$.
- On $\mathbb{R}^n$ the heat kernel is a Gaussian distribution $\mathcal N(0, t \mathbf{I})$
- Knowing the solution of the heat equation allows us to easily sample the marginal distribution $p_t(x) = \int p_s( x_s ) p_{t|s}(x | x_s) d x_s $
$\Longrightarrow$ On a closed manifold like $\mathrm{SO}(3)$, the heat kernel is not a Gaussian distribution anymore!
Solution of the heat equation on SO(3)
$\Longrightarrow$ Can be robustly approximated by truncation or closed form expressions (Matthies et al. 1988).
Isotropic Gaussian Distribution on SO(3)
- The isotropic Gaussian distribution on SO(3) is defined as: $$\mathcal{IG}_{\mathrm{SO(3)}}(\mathbf{x}; \mathbf{\mu}, \epsilon) = f_\epsilon(\arccos( 2^{-1} \mathrm{tr}(\mathbf{\mu}^T \mathbf{x}) - 1 ) ) $$ where $\mathbf{x}$ and $\mathbf{\mu}$ are rotation matrices and $f_\epsilon$ is the density function with variance $\epsilon$.
- Like the Gaussian distribution, it is closed under convolution, corresponds to the solution of the heat diffusion process on SO(3).
$\Longrightarrow$ Sampling from the marginal distribution at time $t$ becomes very easy: $$x \sim p(x), \mathbf{u} \sim \mathcal{IG}_{\mathrm{SO(3)}}(\mathbf{Id}, \epsilon(t)), \mathbf{x}^\prime = \mathbf{u} \mathbf{x}$$
Denoising Score Matching on SO(3)
- We introduce a neural score estimator $s_\theta(\mathbf{x}, \epsilon) : \text{SO(3)}\times\mathbb{R}^{+ \star} \rightarrow T_{\mathbf{x}}$SO(3). In practice a simple MLP.
![]()
- Similarly to the Euclidean case, we ca define a Denoising Score Matching loss $$ \mathcal{L}_{DSM} = \mathbb{E}_{p_\text{data}(\mathbf{x})} \mathbb{E}_{\epsilon \sim \mathcal{N}(0, \sigma_\epsilon^2)} \mathbb{E}_{p_{|\epsilon|}(\tilde{\mathbf{x}} | \mathbf{x} )} \left[ |\epsilon| \ \parallel s_\theta(\tilde{\mathbf{x}}, \epsilon) - \nabla_{X} \log p_{|\epsilon|}( \tilde{\mathbf{x}} | \mathbf{x}) \parallel_2^2 \right] $$
Sampling by Solving a Differential Equations on the Manifold
- For speed and simplicity, we propose to sample from the trained model using the probability flow ODE: $$ \mathbf{x}_T \sim \mathcal{U}_\text{SO(3)} \qquad ; \qquad \mathrm{d} \mathbf{x}_t = -\frac{1}{2} \frac{\mathrm{d} \epsilon(t)}{\mathrm{d} t} s_\theta(\mathbf{x}_t, \epsilon(t)) \mathrm{d} t $$
- As the ODE evolves, the solution needs to remain on the manifold (which is not a worry on $\mathbb{R}^3$)
- We adopt a Geometric ODE strategy that remains on the manifold by construction.
Consider $d\mathbf{x} = f(\mathbf{x},t) dt$, we use a geometric Heun's method: $$\mathbf{y_1} = h f(\mathbf{x_n}, t_n)$$ $$\mathbf{y_2} = h f(\exp(\frac{1}{2} \mathbf{y_1}) \mathbf{x_n} , t_n + \frac{1}{2} h)$$ $$\mathbf{x_{n+1}} = \exp(\mathbf{y_2)} \mathbf{x_n} $$
Illustration of Reverse ODE On Analytic problem
Results on toy distributions
Jagvaral, Lanusse, Mandelbaum, AAAI 2024
- Unconditional distribution modeling.
![]()
![]()
- Conditional distribution modeling $p(\mathbf{R} | y)$ simply by making the score network conditional $s_\theta( \mathbf{R}, \epsilon, y)$
![]()
Back to our initial problem: Let's make it even more fun with graphs!
Adapted from
the network behind the cosmic web
(credit: Kim Albrecht)
Joint modeling of galaxy properties and orientations with E(3)-GNN and SO(3) Diffusion
Jagvaral, Lanusse, Mandelbaum (2024)
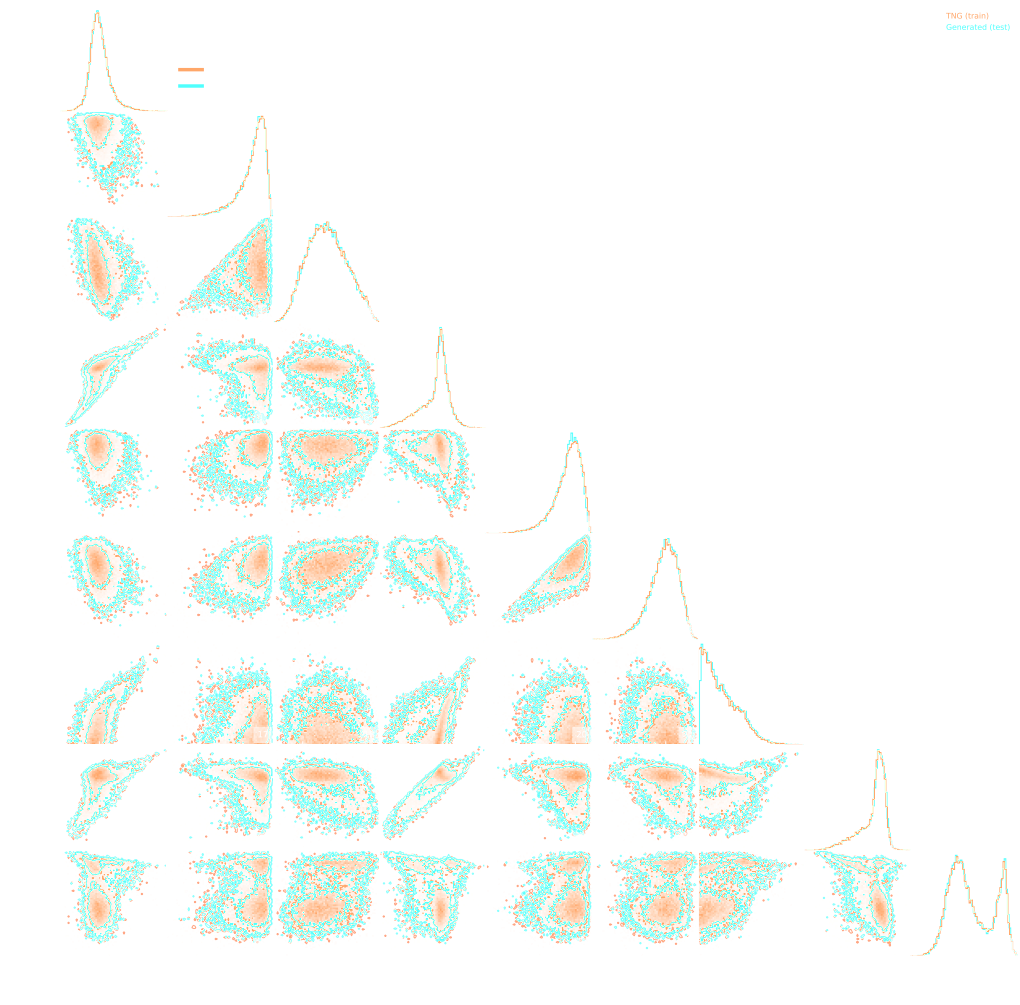
Implicit Inference is easier, cheaper, and yields the same results as Explicit Inference...
But Explicit Inference is cool though...
Credit: Yuuki Omori, Chihway Chang, Justine Zeghal, EiffL
https://github.com/EiffL/LPTLensingComparison
More seriously, Explicit Inference has some advantages:
- More introspectable results to identify systematics
- Allows for fitting parametric corrections/nuisances from data
- Provides validation of statistical inference with a different method
Explicit Inference
Where the JAX things are
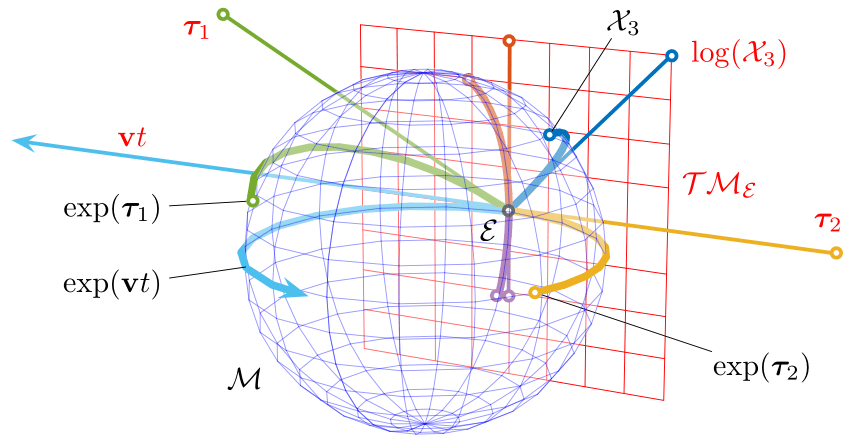
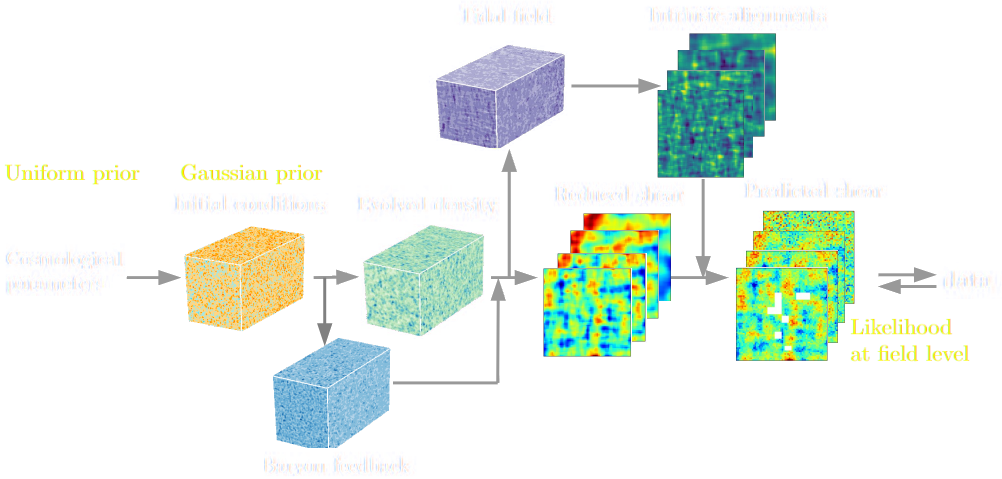
Simulators as Hierarchical Bayesian Models
- If we have access to all latent variables $z$ of the simulator, then the joint log likelihood $p(x | z, \theta)$ is explicit.
- We need to infer the joint posterior $p(\theta, z | x)$ before marginalization to
yield $p(\theta | x) = \int p(\theta, z | x) dz$.
$\Longrightarrow$ Extremely difficult problem as $z$ is typically very high-dimensional. - Necessitates inference strategies with access to gradients of the likelihood. $$\frac{d \log p(x | z, \theta)}{d \theta} \quad ; \quad \frac{d \log p(x | z, \theta)}{d z} $$ For instance: Maximum A Posterior estimation, Hamiltonian Monte-Carlo, Variational Inference.
$\Longrightarrow$ The only hope for explicit cosmological inference is to have fully-differentiable cosmological simulations!
Hybrid Physical-Neural ODEs for Fast N-body Simulations
Work led by:
Denise Lanzieri (now at Sony Computer Science Laboratory)
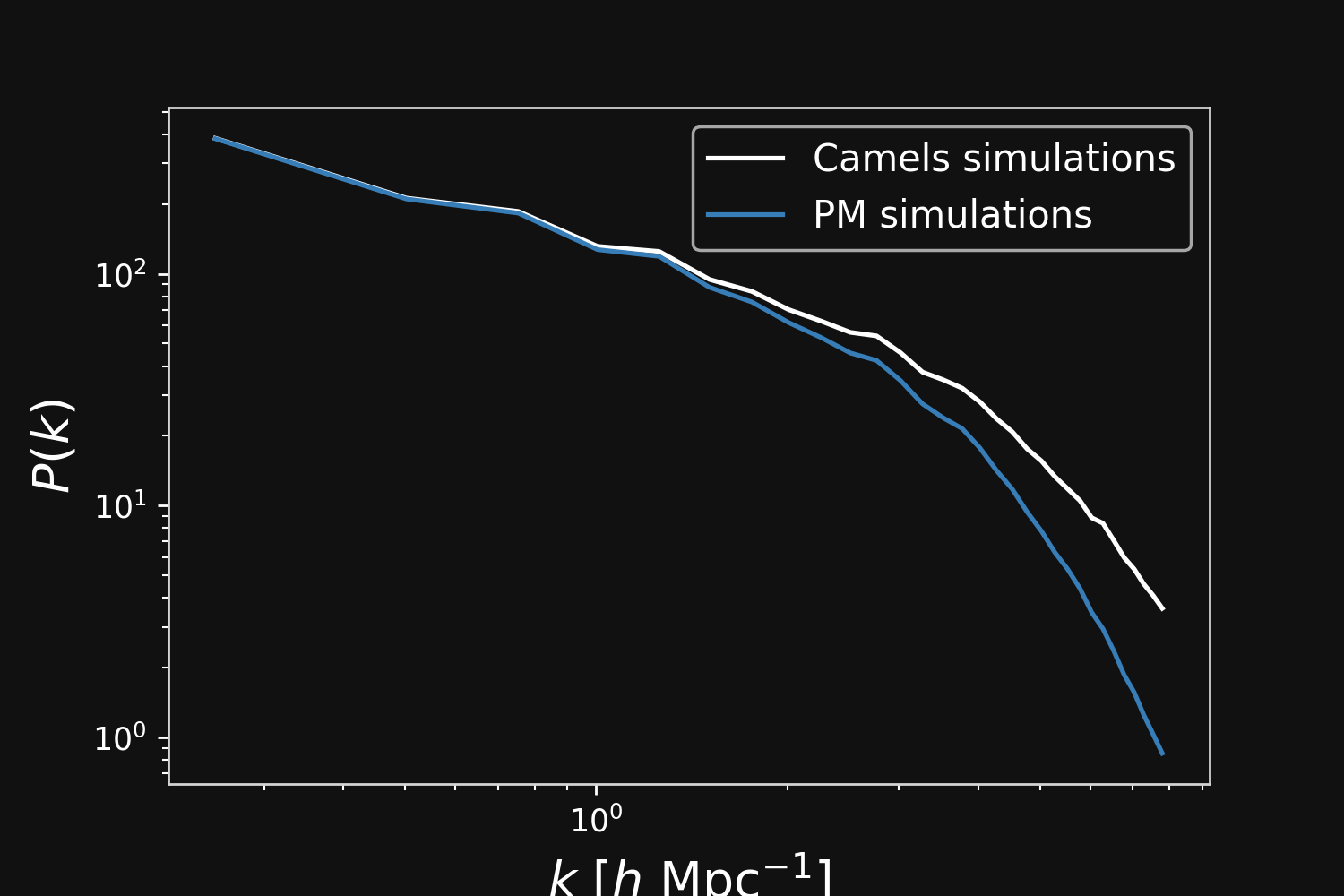
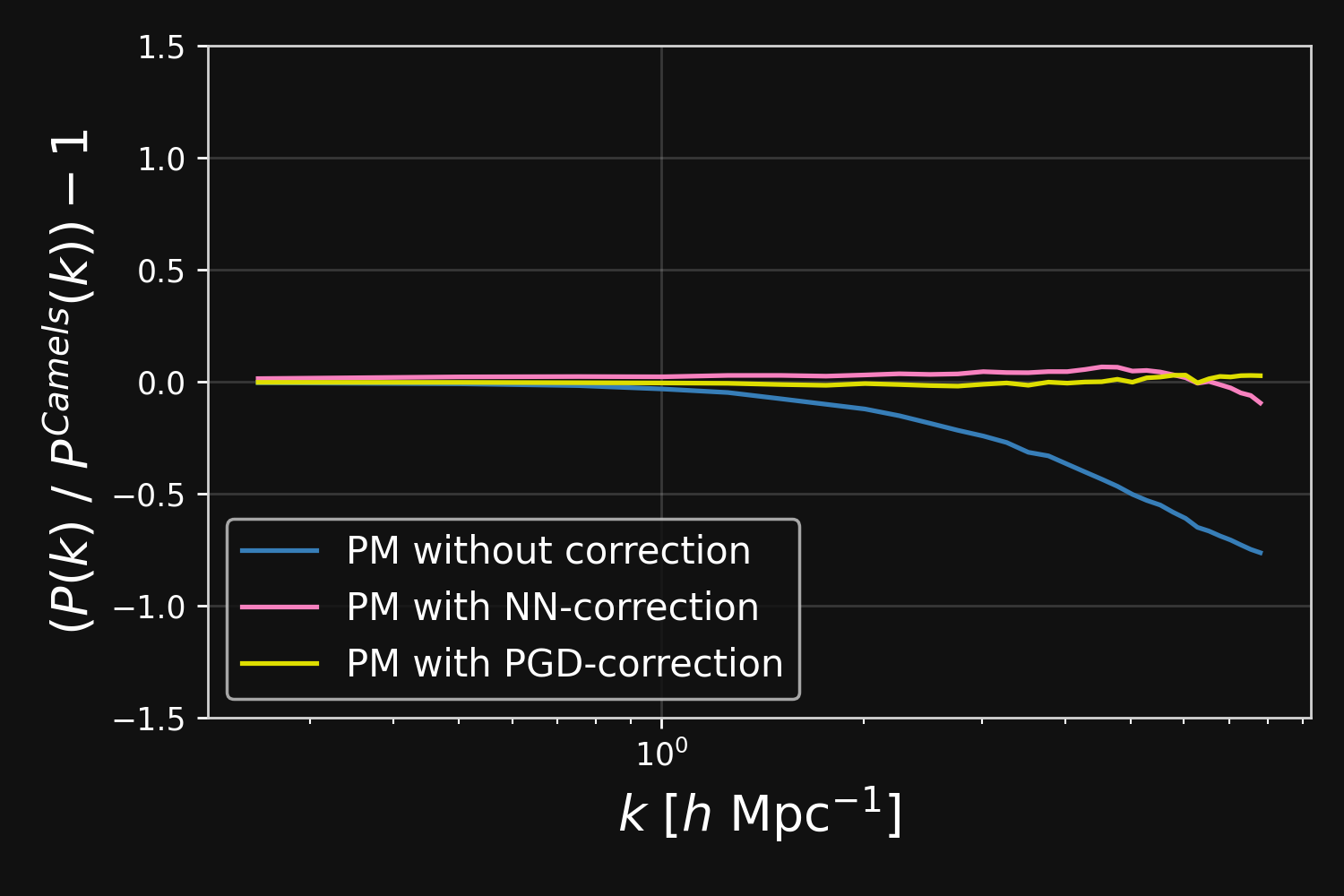
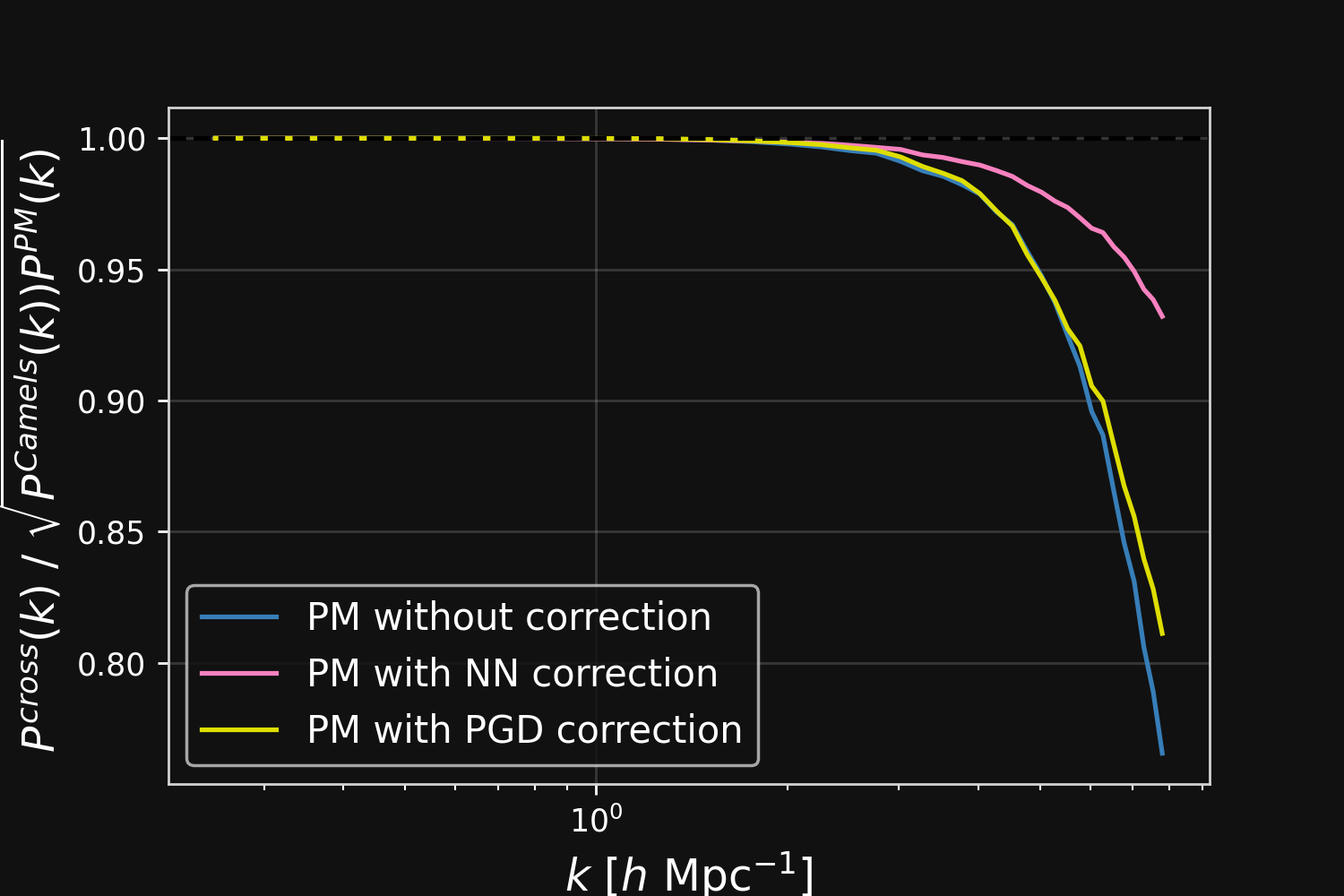
$\Longrightarrow$ Learn residuals to known physical equations to improve accuracy of fast PM simulations.
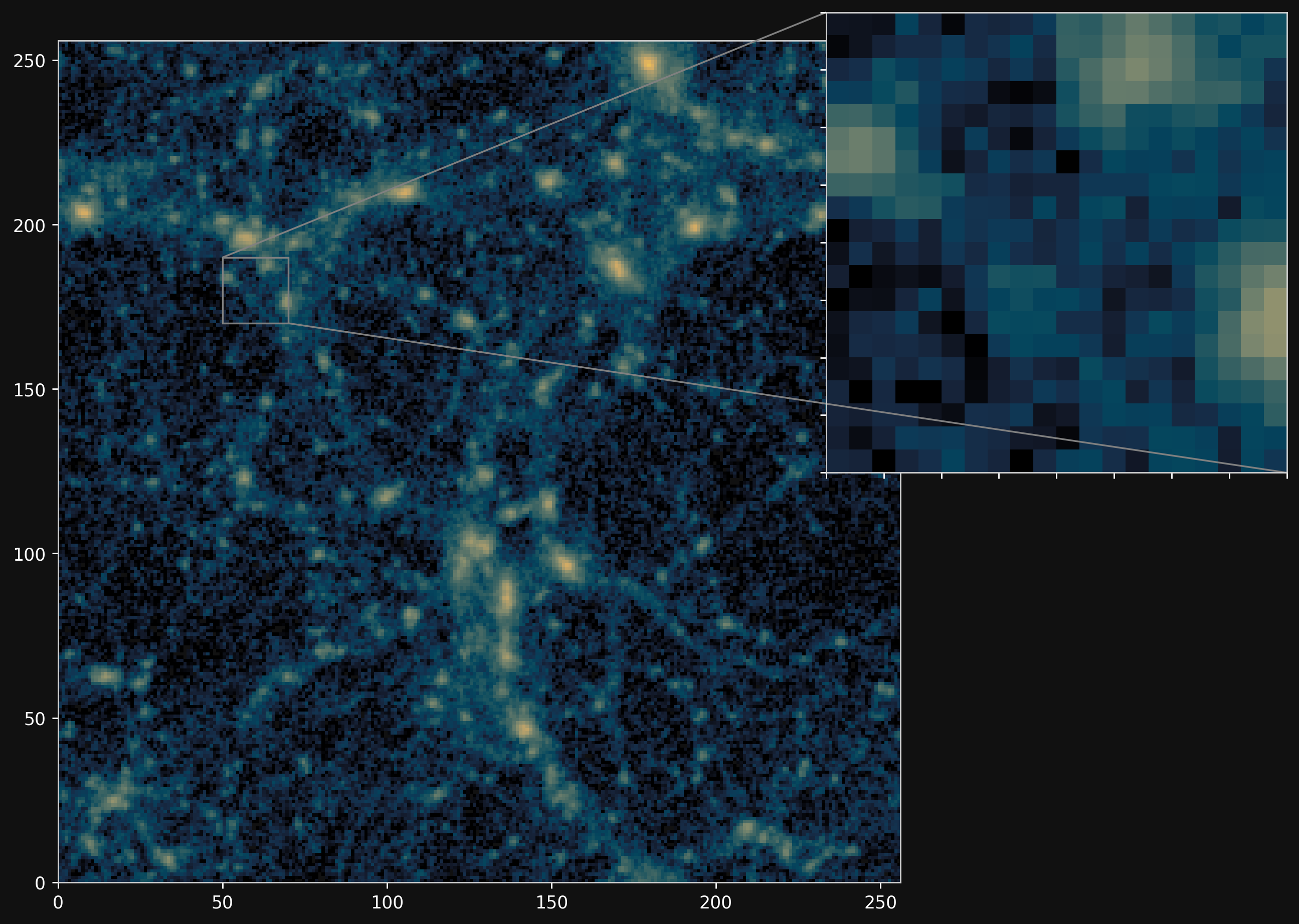
Fill the gap in the accuracy-speed space of PM simulations
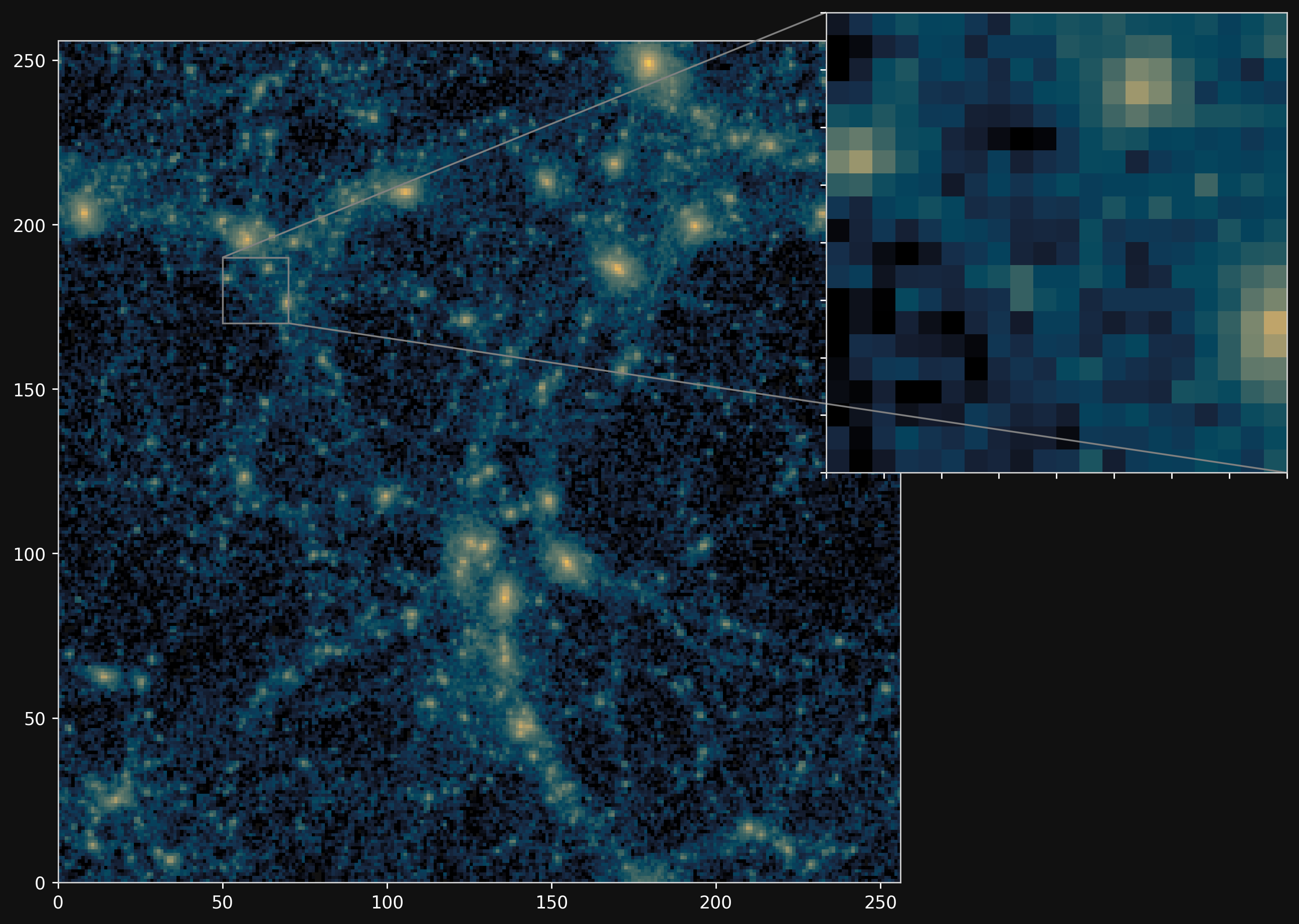
Camels simulations
(differentiable) Particle-Mesh simulations
Hybrid physical/neural differential equations
Lanzieri, Lanusse, Starck (2022)
- $\mathbf{x}$ and $\mathbf{v}$ define the position and the velocity of the particles
- $\phi_{PM}$ is the gravitational potential in the mesh
$\to$ We can use this parametrisation to complement the physical ODE with neural networks.
$$F_\theta(\mathbf{x}, a) = \frac{3 \Omega_m}{2} \nabla \left[ \phi_{PM} (\mathbf{x}) \ast \mathcal{F}^{-1} (1 + \color{#996699}{f_\theta(a,|\mathbf{k}|)}) \right] $$
Correction integrated as a Fourier-based isotropic filter $f_{\theta}$ $\to$ incorporates translation and rotation symmetries
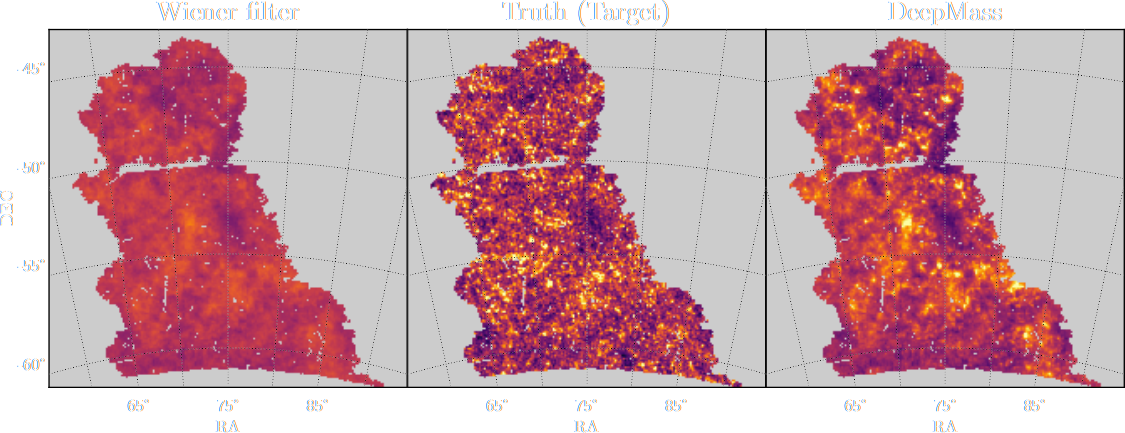
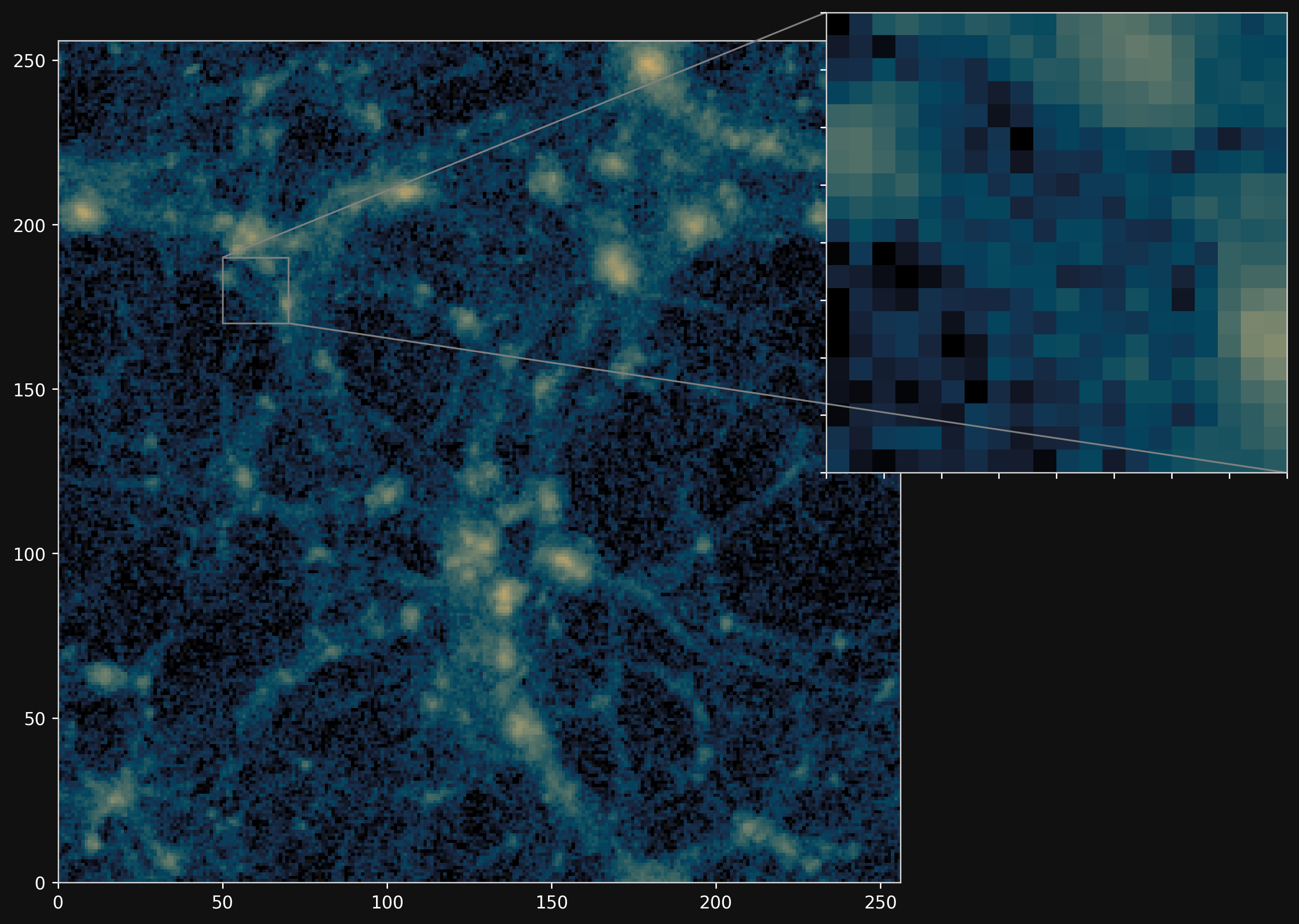
Projections of final density field
Camels simulations
![]()
PM simulations
![]()
PM+NN correction
![]()
Results
Automatically Differentiable High Performance Computing
Work led by:
Wassim Kabalan (PhD Student at IN2P3/APC)
$\Longrightarrow$ Build near compute-optimal distributed simulators in JAX on GPU-based supercomputers
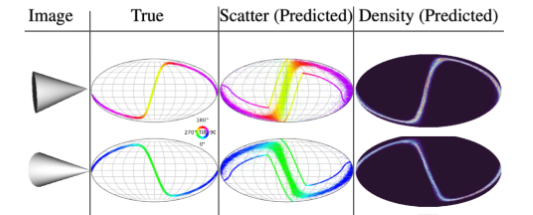
State of the art of differentiable lensing model (Porqueres et al. 2023)
Settings: - 1LPT lightcone
- (1 x 1 x 4.5) $h^{-1}$Gpc
- 64 x 64 x 128 voxels
- 16 x 16 degrees lensing field
- ~2 hours to sample with NUTS on one A100
(our implementation)
Comparison to linear lensing power spectra
$\Longrightarrow$ We need to go bigger!
Mesh FlowPM: Distributed and Automatically Differentiable simulations
Modi, Lanusse, Seljak (2020)
- We developed a Mesh TensorFlow implementation that can scale on GPU clusters.
- Based on low-level NVIDIA NCCL collectives, accessed through Horovod.
- For a $2048^3$ simulation:
- Distributed on 256 NVIDIA V100 GPUs on the Jean Zay supercomputer
- Runtime: ~3 mins
- This is great... but Mesh TensorFlow is now abandonned.
Towards a new generation of JAX-based distributed tools
- JAX v0.4.1 (Dec. 2022) has made a strong push for bringing automated parallelization and support multi-host GPU clusters!
- Scientific HPC still most likely requires dedicated high-performance ops
- jaxDecomp: Domain Decomposition and Parallel FFTs
![]()
- JAX bindings to the high-performance cuDecomp (Romero et al. 2022) adaptive domain decomposition library.
- Provides parallel FFTs and halo-exchange operations.
- Supports variety of backends: CUDA-aware MPI, NVIDIA NCCL, NVIDIA NVSHMEM.
Defining Custom Distributed Ops in JAX
from jax.experimental import mesh_utils
from jax.sharding import PositionalSharding
# Create a Sharding object to distribute a value across devices:
sharding = PositionalSharding(mesh_utils.create_device_mesh((8,)))
# Create an array of random values:
x = jax.random.normal(jax.random.PRNGKey(0), (8192, 8192))
# and use jax.device_put to distribute it across devices:
y = jax.device_put(x, sharding.reshape(4, 2))
jax.debug.visualize_array_sharding(y)
---
┌──────────┬──────────┐
│ TPU 0 │ TPU 1 │
├──────────┼──────────┤
│ TPU 2 │ TPU 3 │
├──────────┼──────────┤
│ TPU 6 │ TPU 7 │
├──────────┼──────────┤
│ TPU 4 │ TPU 5 │
└──────────┴──────────┘
from jaxlib.hlo_helpers import custom_call
def _rms_norm_fwd_cuda_lowering(ctx, x, weight, eps):
[...]
opaque = gpu_ops.create_rms_norm_descriptor([...])
out = custom_call(
b"rms_forward_affine_mixed_dtype",
result_types=[
ir.RankedTensorType.get(x_shape, w_type.element_type),
ir.RankedTensorType.get((n1,), iv_element_type),
],
operands=[x, weight],
backend_config=opaque,
operand_layouts=default_layouts(x_shape, w_shape),
result_layouts=default_layouts(x_shape, (n1,)),
).results
return out
_rms_norm_fwd_p = core.Primitive("rms_norm_fwd")
mlir.register_lowering(
_rms_norm_fwd_p,
_rms_norm_fwd_cuda_lowering,
platform="gpu",
)
def partition(mesh, arg_shapes, result_shape):
result_shardings = jax.tree.map(lambda x: x.sharding, result_shape)
arg_shardings = jax.tree.map(lambda x: x.sharding, arg_shapes)
return mesh, fft, \
supported_sharding(arg_shardings[0], arg_shapes[0]), \
(supported_sharding(arg_shardings[0], arg_shapes[0]),)
def infer_sharding_from_operands(mesh, arg_shapes, result_shape):
arg_shardings = jax.tree.map(lambda x: x.sharding, arg_shapes)
return supported_sharding(arg_shardings[0], arg_shapes[0])
@custom_partitioning
def my_fft(x):
return fft(x)
my_fft.def_partition(
infer_sharding_from_operands=infer_sharding_from_operands,
partition=partition)
JAX cuDecomp interface led by Wassim Kabalan (IN2P3/APC)
- JAX>=v0.4.1 defines sharded tensors and a "computation follows data" philosophy.
- jaxlib provides a helper to define custom CUDA lowering
- Recent API allows us to define custom partitioning schemes compatible with a primitive
Building PM components from these distributed operations
Kabalan, Lanusse, Boucaud (in prep.)
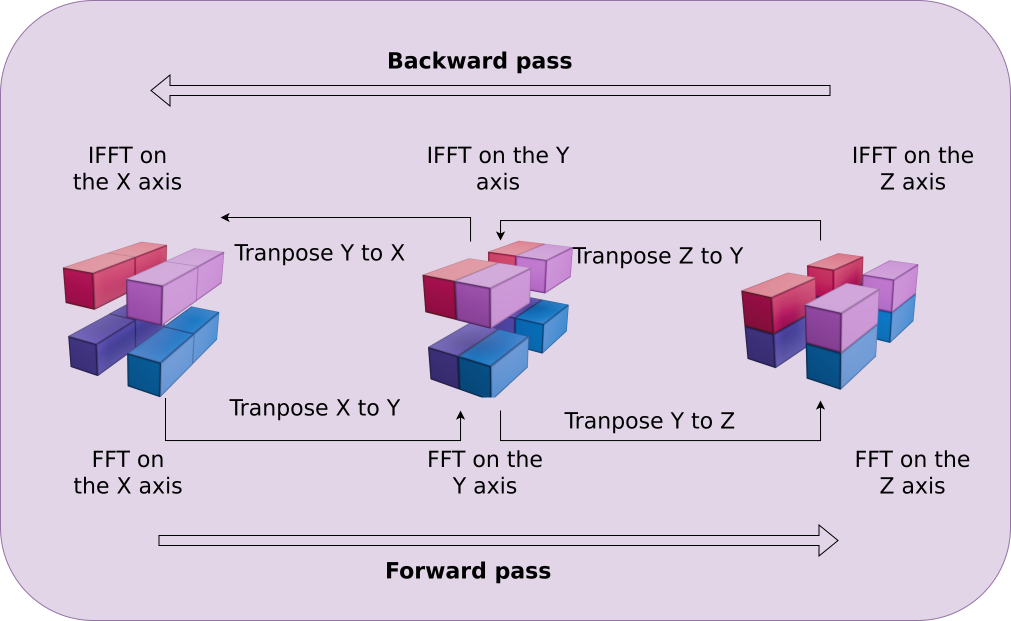
Distributed 3D FFT for force computation
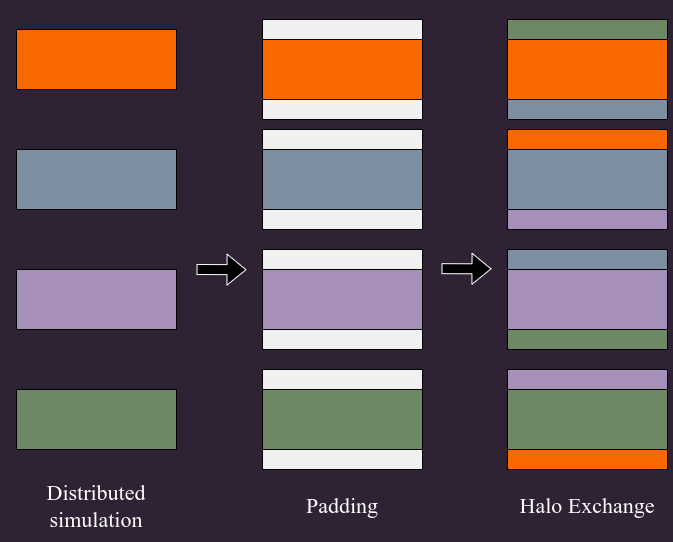
Halo Exchange for CiC painting and reading
$2048^3$ LPT field, 1.02s on 32 H100 GPUs
Performance Benchmark
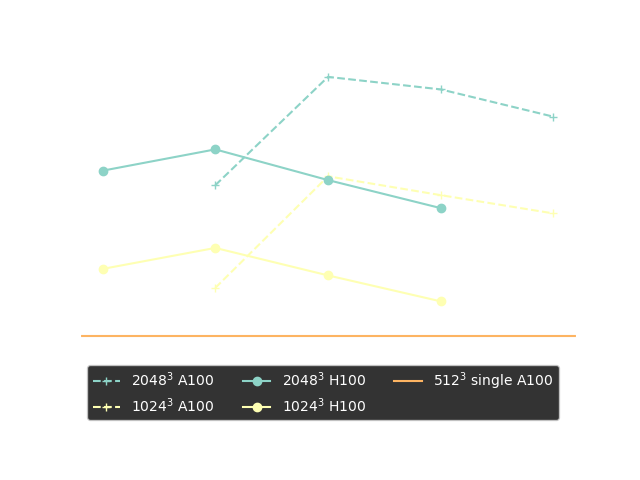
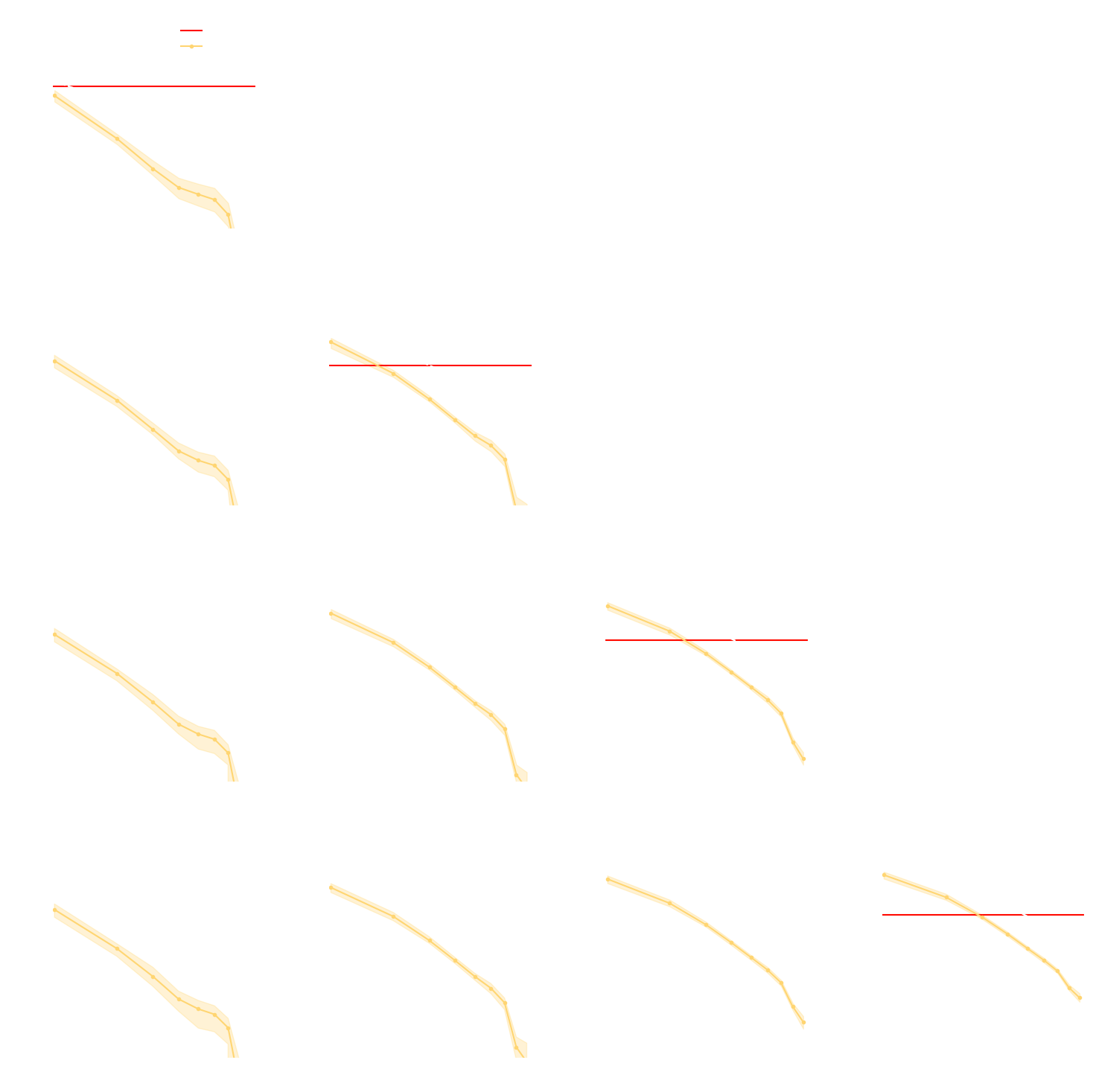
Strong scaling plots of 3D FFT
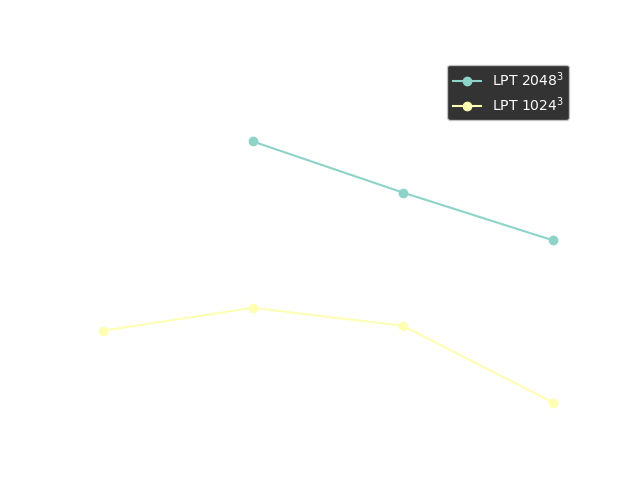
Timing of 1LPT computation
Conclusion
Conclusion
Full-Field Explicit Inference for Cosmological Inference
- A change of paradigm from analytic likelihoods to simulators as physical model.
- Progress in differentiable simulators and inference methodology paves the way to full inference over probabilistic model.
- Still subject to a number of outstanding challenges
- Technical Challenges: model distribution on large-scale GPU supercomputers
- Methodological Challenges: scalable inference methods for high-dimensional and potentially multimodal posteriors.
- Modeling Challenges: more realistic and data-driven forward models while remaining fast and differentiable.
- Ultimately, promises optimal exploitation of cosmological surveys.
Call to action: If you are interested in contributing to building JAX-based HPC tools, please get in touch :-) !
Thank you!
On the topic of JAX codes...
Jax-GalSim: it's GalSim, but Differentiable and GPU-accelerated!
import jax_galsim as galsim
psf_beta = 5 #
psf_re = 1.0 # arcsec
pixel_scale = 0.2 # arcsec / pixel
sky_level = 2.5e3 # counts / arcsec^2
# Define the galaxy profile.
gal = galsim.Exponential(flux=1, scale_radius=2).shear(g1=.3, g2=.4)
gal = gal.shear(g1=0.01, g2=0.05)
# Define the PSF profile.
psf = galsim.Gaussian(flux=1., half_light_radius=psf_re)
# Final profile is the convolution of these.
final = galsim.Convolve([gal, psf])
# Draw the image with a particular pixel scale.
image = final.drawImage(scale=pixel_scale)
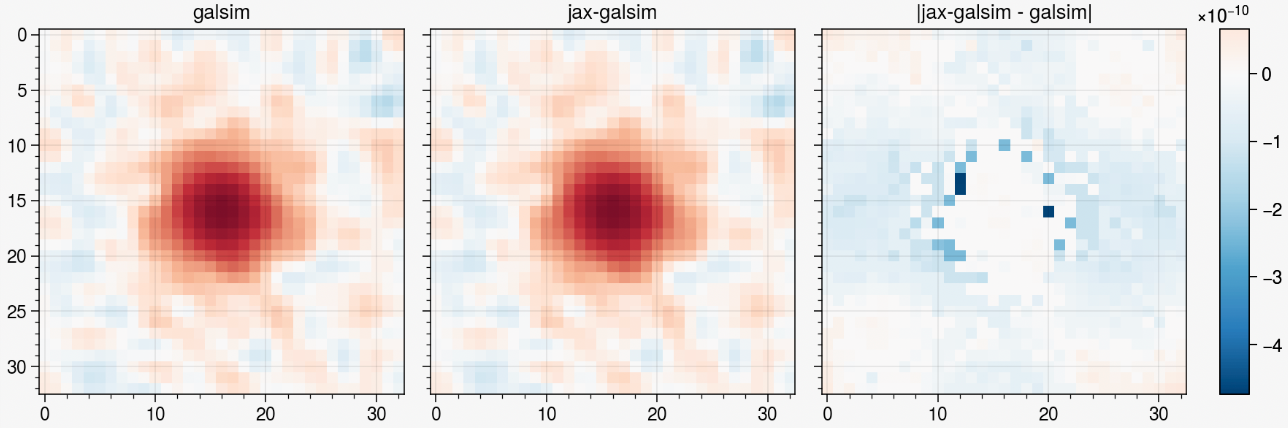
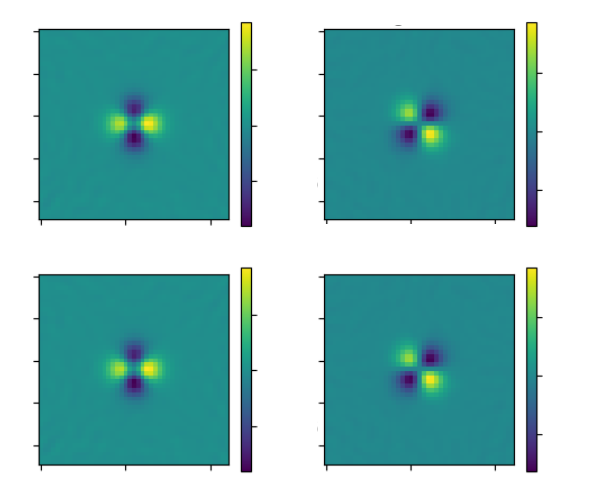
metacalibration residuals, credit: Matt Becker
Guiding principles:
- Strictly follows the GalSim API.
- Validated against GalSim up to numerical accuracy: inherits from GalSim's test suite
- Implementations should be easy to read and understand.
Example use-case: Metacalibration in 3 lines of code!
@jax.jacfwd
def autometacal(shear, image, psf, rec_psf):
# Step 1: Deconvolve the image
deconvolved = jax_galsim.Convolve([image,
jax_galsim.Deconvolve(psf)])
# Step 2: Apply shear
sheared = deconvolved.shear(g1=shear[0], g2=shear[1])
# Step 3: Reconvolve by slightly dilated PSF
reconvolve = jax_galsim.Convolve([sheared, rec_psf])
return reconvolve.drawImage(scale=scale, method='no_pixel').array
