Merging deep learning with physical models
for the analysis of modern cosmological surveys
François Lanusse



slides at eiffl.github.io/talks/Oxford2020
the $\Lambda$CDM view of the Universe



the Rubin Observatory Legacy Survey of Space and Time
- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed $\sim1000$ times
Previous generation survey: SDSS
Image credit: Peter Melchior
Current generation survey: DES
Image credit: Peter Melchior
LSST precursor survey: HSC
Image credit: Peter Melchior
The challenges of modern surveys
$\Longrightarrow$ Modern surveys will provide large volumes of high quality data
A Blessing
- Unprecedented statistical power
- Great potential for new discoveries
A Curse
- Existing methods are reaching their limits at every step of the science analysis
- Control of systematics is paramount
LSST forecast on dark energy parameters
![]()
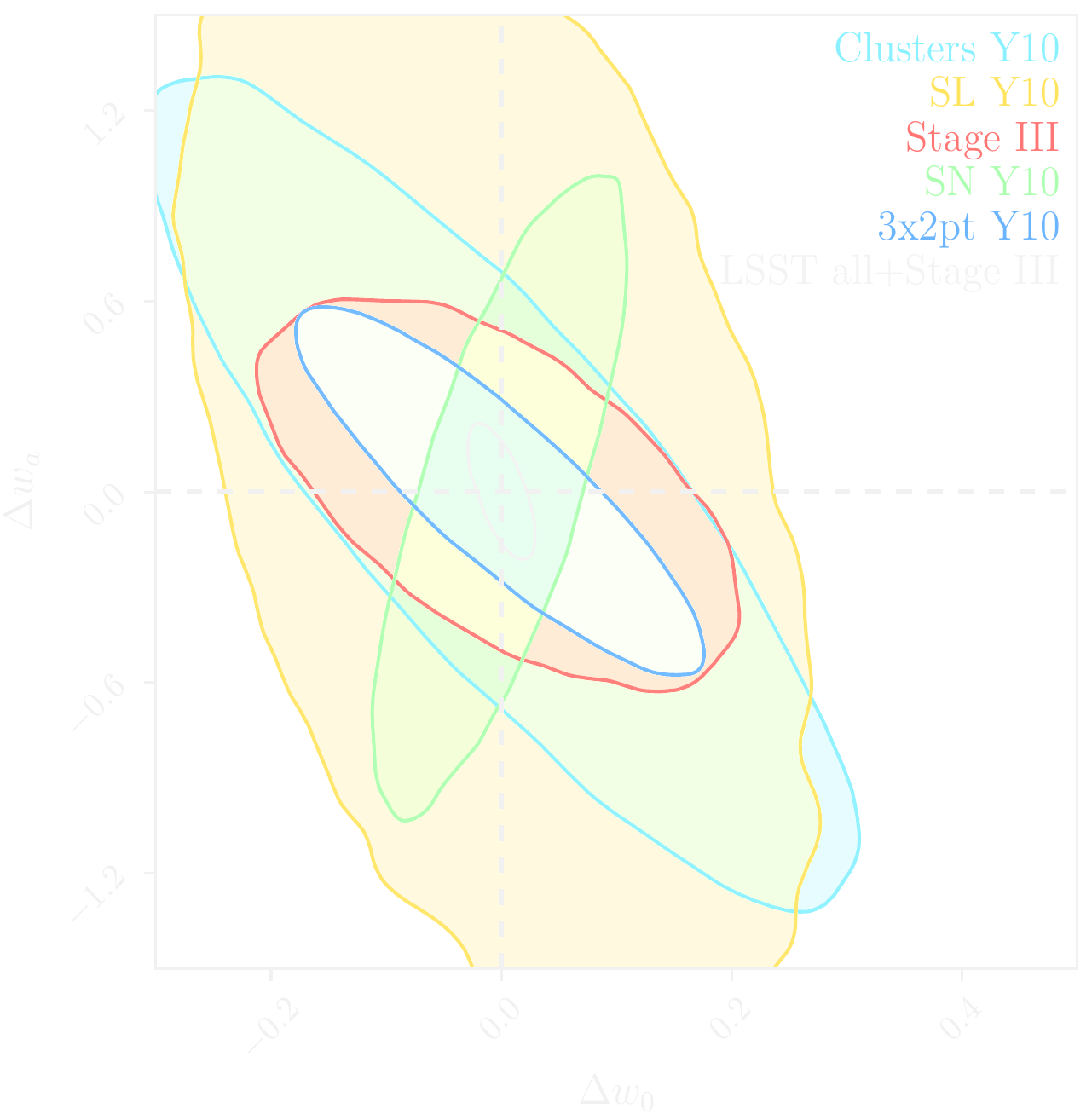
$\Longrightarrow$ Dire need for novel analysis techniques to fully realize the potential of modern surveys.
Can AI solve all of our problems?
Branched GAN model for deblending (Reiman & Göhre, 2018)
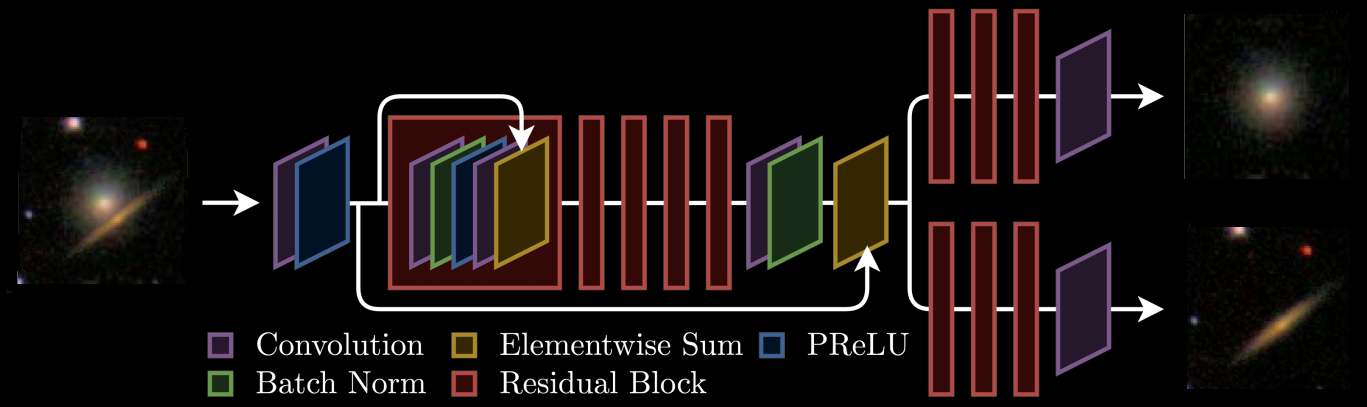
The issue with using deep learning as a black-box
- No explicit control of noise, PSF, depth, number of sources.
- Model would have to be retrained for all observing configurations
- No guarantees on the network output (e.g. flux preservation, artifacts)
- No proper uncertainty quantification.

Outline of this talk
How can we merge Deep Learning and Physical Models to help us make sense
of increasingly complex data?
- Generative Models for Galaxy Image Simulations
- Differentiable models of the Large Scale Structure
- Differentiable cosmological computations
Deep Generative Models for Galaxy Image Simulations

Work in collaboration with
Rachel Mandelbaum, Siamak Ravanbakhsh, Chun-Liang Li, Barnabas Poczos, Peter Freeman
Lanusse et al. (2020)
Ravanbakhsh, Lanusse, et al. (2017)
Ravanbakhsh, Lanusse, et al. (2017)
The weak lensing shape measurement problem
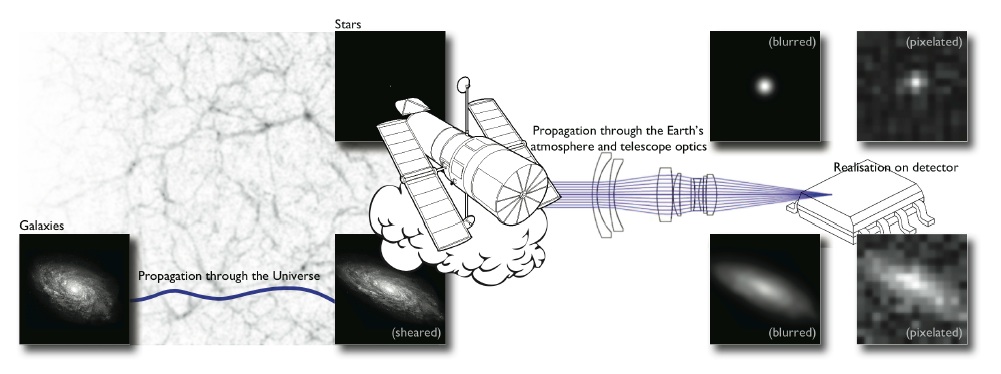
Shape measurement biases
$$ < e> = \ (1 + m) \ \gamma \ + \ c $$
- Can be calibrated on image simulations
- How complex do the simulations need to be?
Impact of galaxy morphology

Mandelbaum, et al. (2013), Mandelbaum, et al. (2014)
The need for data-driven generative models
- Lack or inadequacy of physical model
- Extremely computationally expensive simulations
Can we learn a model for the signal from the data itself?
The evolution of generative models




- Deep Belief Network
(Hinton et al. 2006) - Variational AutoEncoder
(Kingma & Welling 2014) - Generative Adversarial Network
(Goodfellow et al. 2014) - Wasserstein GAN
(Arjovsky et al. 2017)
Complications specific to astronomical images: spot the differences!

CelebA

HSC PDR-2 wide
- There is noise
- We have a Point Spread Function
A Physicist's approach: let's build a model





$\longrightarrow$
$g_\theta$
$g_\theta$
$\longrightarrow$
PSF
PSF
$\longrightarrow$
Pixelation
Pixelation
$\longrightarrow$
Noise
Noise


Probabilistic model
$$ x \sim ? $$
$$ x \sim \mathcal{N}(z, \Sigma) \quad z \sim ? $$
latent $z$ is a denoised galaxy image
latent $z$ is a denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} z, \Sigma) \quad z \sim ?$$
latent $z$ is a super-resolved and denoised galaxy image
latent $z$ is a super-resolved and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast z), \Sigma) \quad z \sim ? $$
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast g_\theta(z)), \Sigma) \quad z \sim \mathcal{N}(0, \mathbf{I}) $$
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
$\Longrightarrow$ Decouples the morphology model from the observing conditions.
How to train your dragon model
- Training the generative amounts to finding $\theta_\star$ that
maximizes the marginal likelihood of the model:
$$p_\theta(x | \Sigma, \Pi) = \int \mathcal{N}( \Pi \ast g_\theta(z), \Sigma) \ p(z) \ dz$$
$\Longrightarrow$ This is generally intractable
- Efficient training of parameter $\theta$ is made possible by Amortized Variational Inference.
Auto-Encoding Variational Bayes (Kingma & Welling, 2014)
- We introduce a parametric distribution $q_\phi(z | x, \Pi, \Sigma)$ which aims to model the posterior $p_{\theta}(z | x, \Pi, \Sigma)$.
- Working out the KL divergence between these two distributions leads to: $$\log p_\theta(x | \Sigma, \Pi) \quad \geq \quad - \mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]$$ $\Longrightarrow$ This is the Evidence Lower-Bound, which is differentiable with respect to $\theta$ and $\phi$.
Illustration on HST/ACS COSMOS images

Fitting observations with VAE and Bulge+Disk parametric model.
- Training set: GalSim COSMOS HST/ACS postage stamps
- 80,000 deblended galaxies from I < 25.2 sample
- Drawn on 128x128 stamps at 0.03 arcsec resolution
- Each stamp comes with:
- PSF
- Noise power spectrum
- Bulge+Disk parametric fit
- Auto-Encoder model:
- Deep residual autoencoder:
7 stages of 2 resnet blocs each - Dense bottleneck of size 16.
- Outputs positive, noiseless, deconvolved, galaxy surface brightness.
- Deep residual autoencoder:
- Generative models are conditioned on:
mag_auto, flux_radius, zphot
Flow-VAE samples

Second order moments

Testing conditional sampling

$\Longrightarrow$ We can successfully condition galaxy generation.
Testing galaxy morphologies

Going one step further: generative models as data-driven priors
$\boxed{y = \mathbf{A}x + n}$
$\mathbf{A}$ is known and encodes our physical understanding of the problem.
$\Longrightarrow$ When non-invertible or ill-conditioned, the inverse problem is ill-posed with no unique solution $x$
$y$
![]()
Simulated Rubin Observatory

Simulated Rubin Observatory
$$ = \qquad \Pi \qquad \ast $$
$x$
![]()
Hubble Space Telescope

Hubble Space Telescope
$$+ \qquad n$$
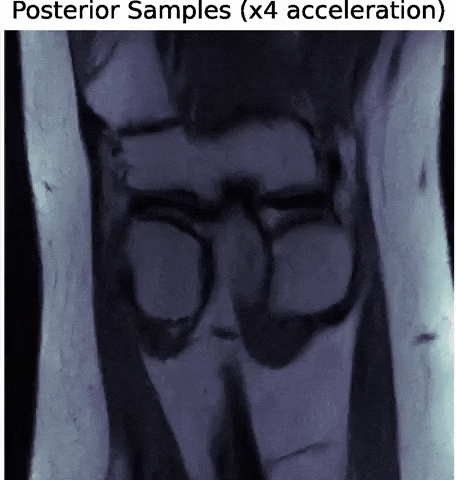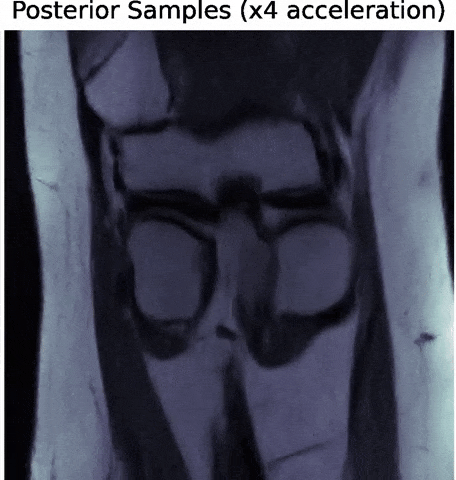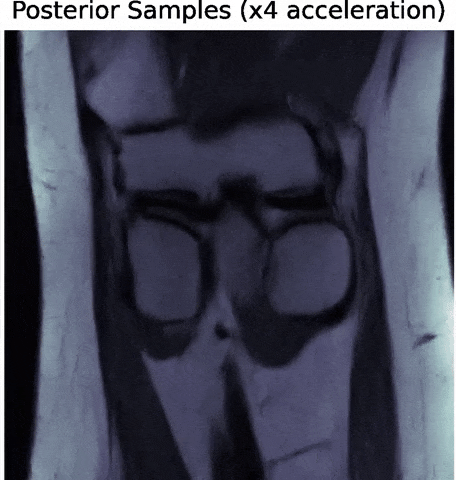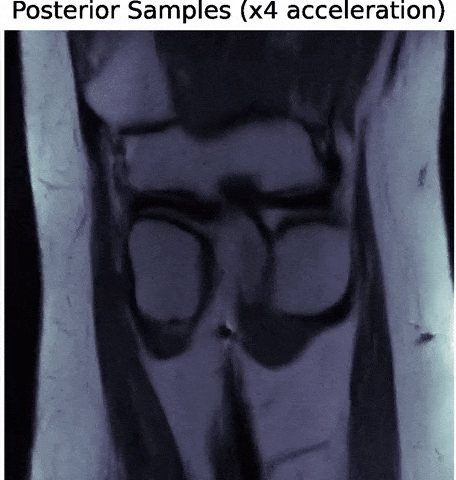
Bayesian Inference a.k.a. Uncertainty Quantification
The Bayesian view of the problem:
$$ p(z | x ) \propto p_\theta(x | z, \Sigma, \mathbf{\Pi}) p(z)$$
where:
- $p( z | x )$ is the posterior
- $p( x | z )$ is the data likelihood, contains the physics
- $p( z )$ is the prior


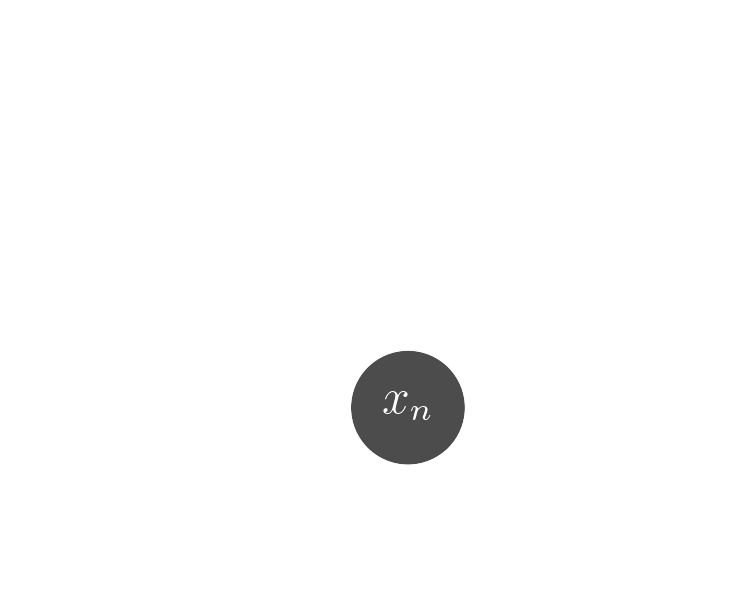
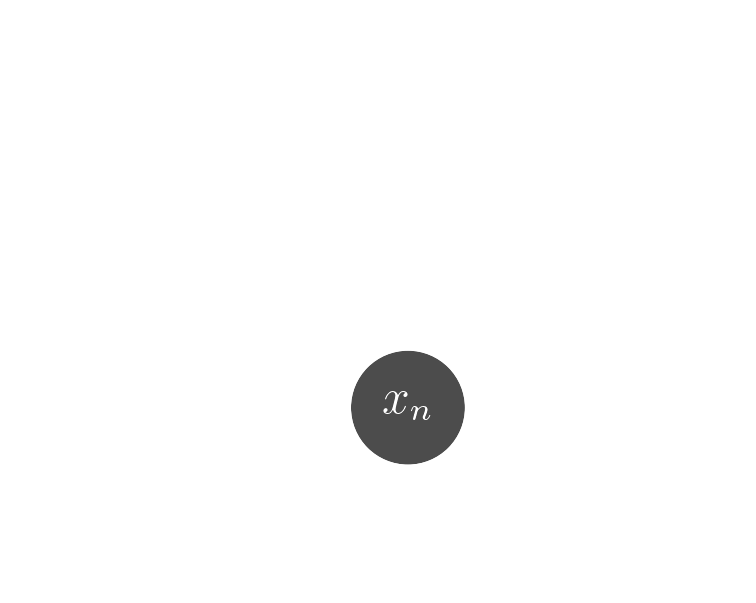
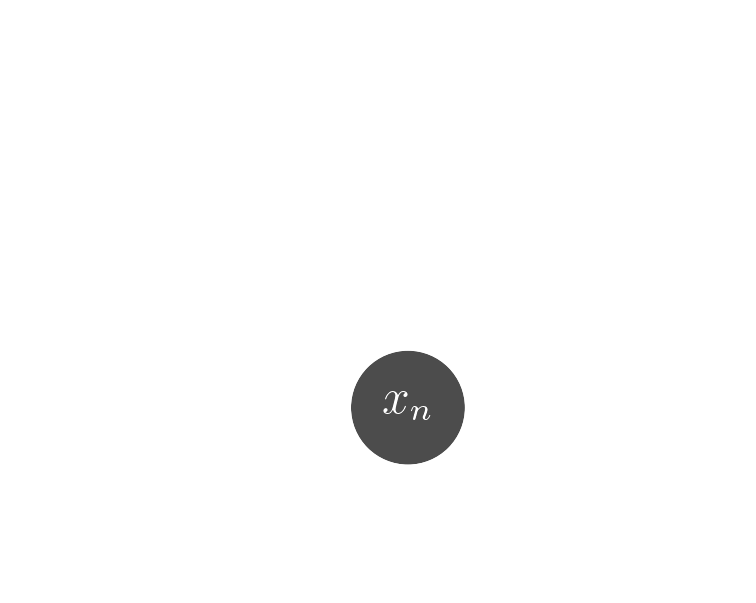
Data
$x_n$
$x_n$
Truth
$x_0$
$x_0$
Posterior samples
$g_\theta(z)$
$g_\theta(z)$

$\mathbf{P} (\Pi \ast g_\theta(z))$
Median

Data residuals
$x_n - \mathbf{P} (\Pi \ast g_\theta(z))$
$x_n - \mathbf{P} (\Pi \ast g_\theta(z))$
Standard Deviation
$\Longrightarrow$ Uncertainties are fully captured by the posterior.
Examples of applications of generative models
- Hybrid Physical-Deep Learning Model for Astronomical Inverse Problems
F. Lanusse, P. Melchior, F. Moolekamp
$\mathcal{L} = \frac{1}{2} \parallel \mathbf{\Sigma}^{-1/2} (\ Y - P \ast A S \ ) \parallel_2^2 - \sum_{i=1}^K \log p_{\theta}(S_i)$

- Denoising Score-Matching for Uncertainty Quantification in Inverse Problems
Z. Ramzi, B. Remy, F. Lanusse, P. Ciuciu, J.L. Starck
Takeaway message
- We have combined physical and deep learning components to model
observed noisy and PSF-convolved galaxy images.
$\Longrightarrow$ This framework can handle multi-band, multi-resolution, multi-instrument data. - Once trained, generative models can be used as data-driven priors for various inverse problems: denoising, deblending, deconvoluion, etc....
$\Longrightarrow$ This Bayesian framework allows for robust uncertainty quantification.
GalSim Hub

- Framework for sampling from deep generative models directly from within GalSim.
- Go check out the beta version: https://github.com/McWilliamsCenter/galsim_hub
Differentiable models of the Large-Scale Structure

Work in collaboration with
Chirag Modi, Uroš Seljak
Modi, Lanusse, Seljak, et al., in prep
Modi, et al. (2018)
Modi, et al. (2018)
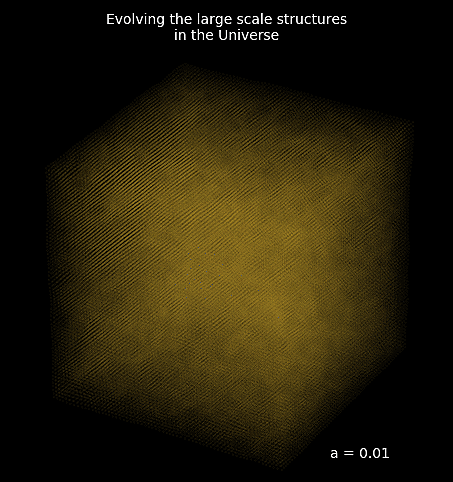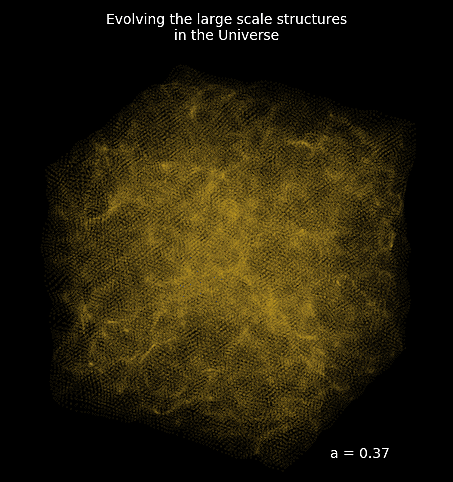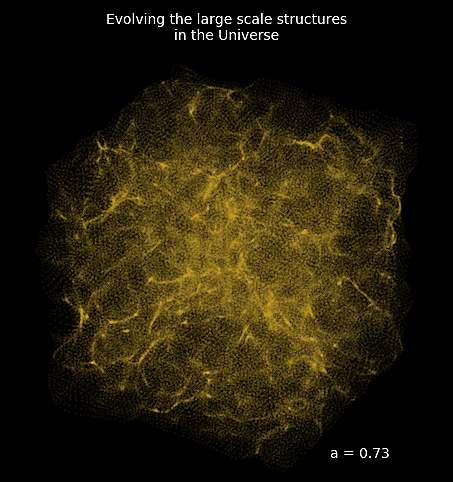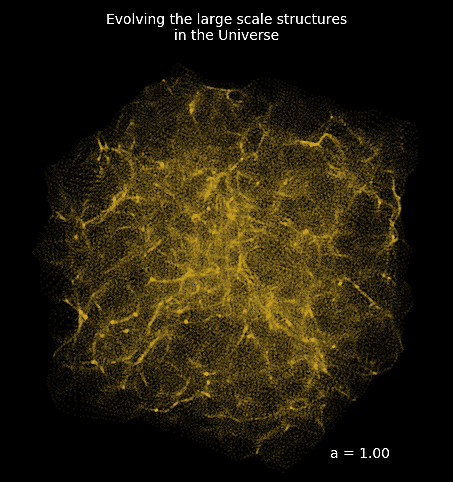
traditional cosmological inference
HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
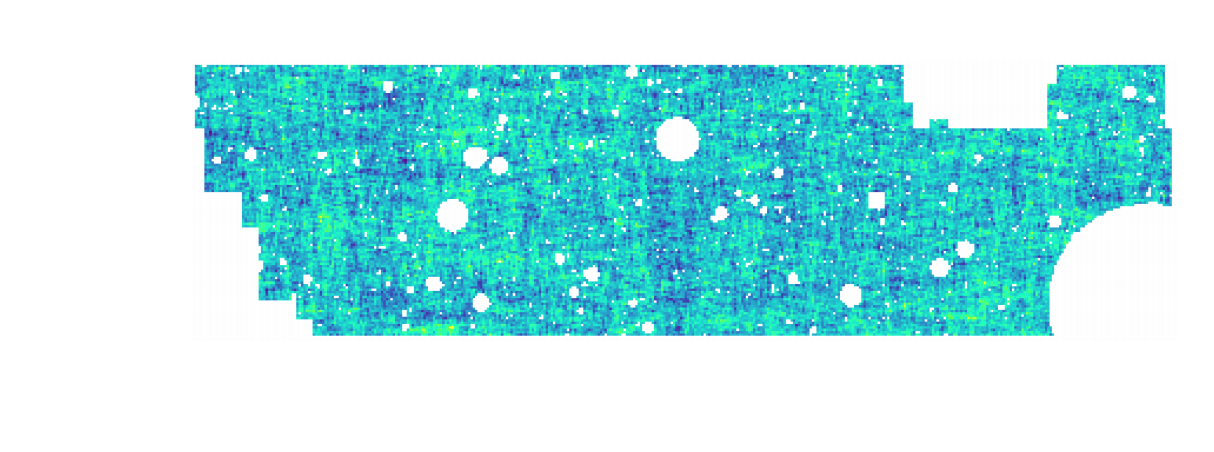
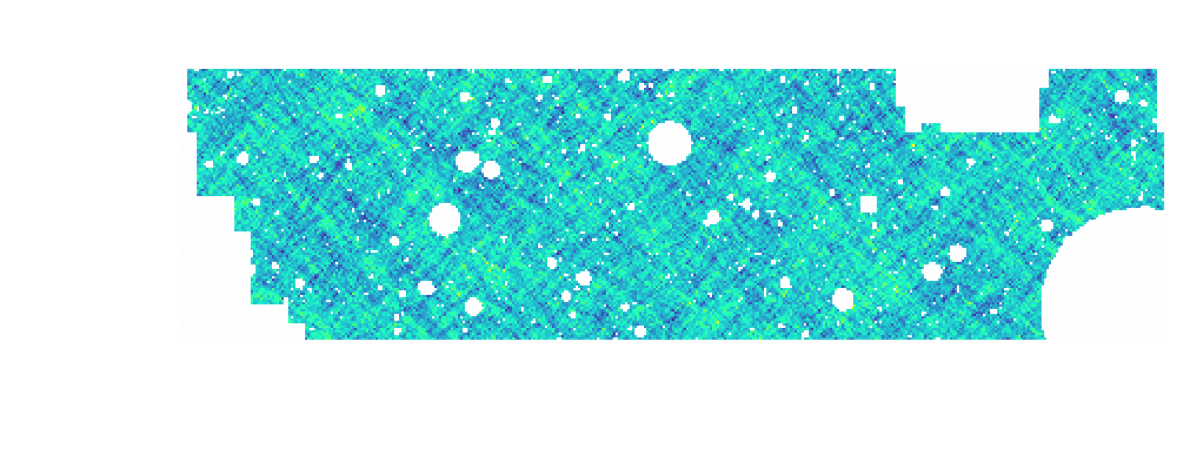
(Hikage,..., Lanusse, et al. 2018)
- Measure the ellipticity $\epsilon = \epsilon_i + \gamma$ of all galaxies
$\Longrightarrow$ Noisy tracer of the weak lensing shear $\gamma$ - Compute summary statistics based on 2pt functions,
e.g. the power spectrum - Run an MCMC to recover a posterior on model parameters, using an analytic likelihood $$ p(\theta | x ) \propto \underbrace{p(x | \theta)}_{\mathrm{likelihood}} \ \underbrace{p(\theta)}_{\mathrm{prior}}$$
Main limitation: the need for an explicit likelihood
We can only compute the likelihood for simple summary statistics and on large scales
$\Longrightarrow$ We are dismissing most of the information!
A different road: forward modeling
- Instead of trying to analytically evaluate the likelihood, let us build a forward model of the observables.
- Each component of the model is now tractable, but at the cost of a large number of latent variables.
$\Longrightarrow$ How to peform efficient inference in this large number of dimensions?
- A non-exhaustive list of methods:
- Hamiltonian Monte-Carlo
- Variational Inference
- MAP+Laplace
- Gold Mining
- Dimensionality reduction by Fisher-Information Maximization
What do they all have in common?
-> They require fast, accurate, differentiable forward simulations
-> They require fast, accurate, differentiable forward simulations
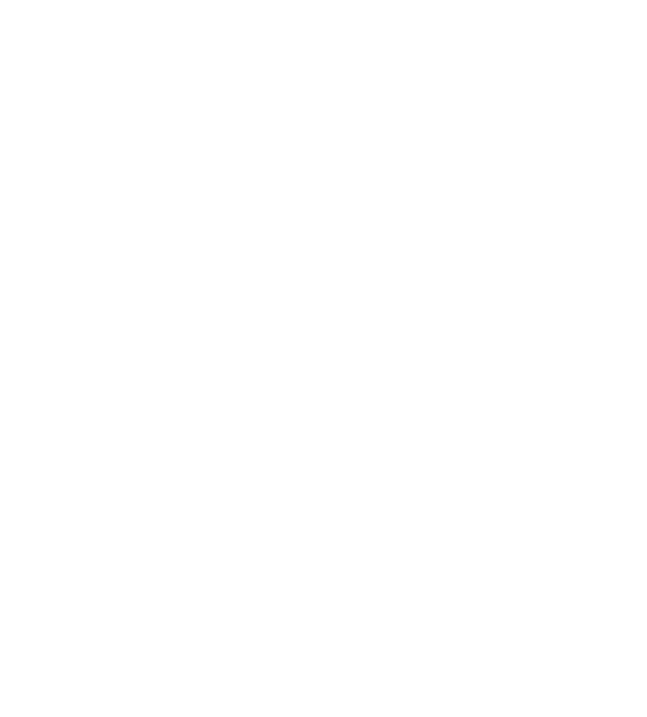
(Schneider et al. 2015)
How do we simulate the Universe in a fast and differentiable way?
Forward Models in Cosmology
 Linear Field
Linear Field
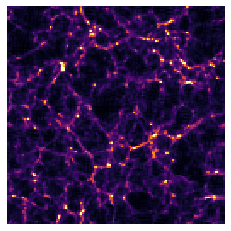 Final Dark Matter
Final Dark Matter
 Dark Matter Halos
Dark Matter Halos
 Galaxies
Galaxies
$\longrightarrow$
N-body simulations
$\longrightarrow$
Group Finding
algorithms
Group Finding
algorithms
$\longrightarrow$
Semi-analytic &
distribution models
Semi-analytic &
distribution models
You can try to learn the simulation...
Learning particle displacement with a UNet. S. He, et al. (2019)

The issue with using deep learning as a black-box
- No guarantees to work outside of training regime.
- No guarantees to capture dependence on cosmology accurately.
the Fast Particle-Mesh scheme for N-body simulations
The idea: approximate gravitational forces by estimating densities on a grid.- The numerical scheme:
- Estimate the density of particles on a mesh
=> compute gravitational forces by FFT - Interpolate forces at particle positions
- Update particle velocity and positions, and iterate
- Estimate the density of particles on a mesh
- Fast and simple, at the cost of approximating short range interactions.

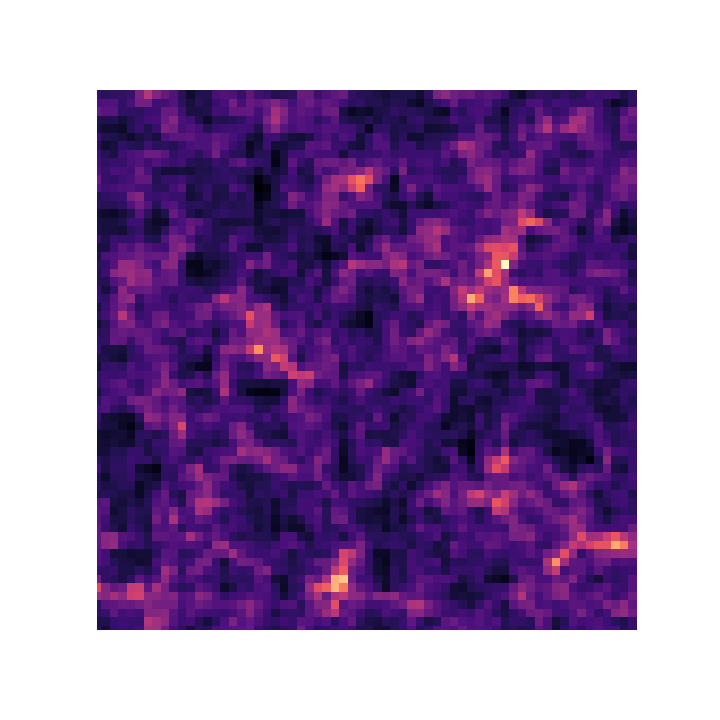


$\Longrightarrow$ Only a series of FFTs and interpolations.
introducing FlowPM: Particle-Mesh Simulations in TensorFlow

import tensorflow as tf
import flowpm
# Defines integration steps
stages = np.linspace(0.1, 1.0, 10, endpoint=True)
initial_conds = flowpm.linear_field(32, # size of the cube
100, # Physical size
ipklin, # Initial powerspectrum
batch_size=16)
# Sample particles and displace them by LPT
state = flowpm.lpt_init(initial_conds, a0=0.1)
# Evolve particles down to z=0
final_state = flowpm.nbody(state, stages, 32)
# Retrieve final density field
final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions),
final_state[0])
with tf.Session() as sess:
sim = sess.run(final_field)
- Seamless interfacing with deep learning components
- Mesh TensorFlow implementation for distribution on supercomputers

Example use-case: reconstructing initial conditions by MAP optimization

Going back to simpler times...
$$\arg\max_z \ \log p(x_{dm} = f(z)) \ + \ p(z) $$
where:
- $f$ is FlowPM
- $z$ are the initial conditions (early universe)
- $x_{dm}$ is the present day dark matter distribution
MAP optimization in action
$$\arg\max_z \ \log p(x_{dm} = f(z)) \ + \ p(z) $$credit: C. Modi
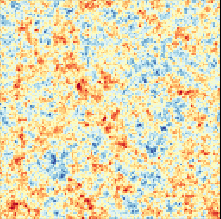
True initial conditions
$z_0$

Reconstructed initial conditions $z$

Reconstructed dark matter distribution $x = f(z)$

Data
$x_{DM} = f(z_0)$
Check out this blogpost for more details
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html
Forward Models in Cosmology
 Linear Field
Linear Field
 Final Dark Matter
Final Dark Matter
 Dark Matter Halos
Dark Matter Halos
 Galaxies
Galaxies
$\longrightarrow$
N-body simulations
FlowPM
N-body simulations
FlowPM
$\longrightarrow$
Group Finding
algorithms
Group Finding
algorithms
$\longrightarrow$
Semi-analytic &
distribution models
Semi-analytic &
distribution models
Example of Extending Dark Matter Simulations with Deep Learning

$\longrightarrow$


Modi et al. 2018
The practical challenge for inference at scale
- Simulations of scientifically interesting sizes do not fit on a single GPU RAM
e.g. $128^3$ operational, need $1024^3$ for survey volumes
$\Longrightarrow$ We need a distributed Machine Learning Framework
- Most common form of distribution is data-parallelism $\Longrightarrow$ Reached Exascale on scientific deep learning applications
- What we need is model-parallelism on HPC environments

$\Longrightarrow$ We have investigatded the Mesh TensorFlow framework on the NERSC Cori machine and Google TPUs.
Mesh TensorFlow in a few words
- Redefines the TensorFlow API, in terms of abstract logical tensors with actual memory instantiation on multiple devices.
(Gholami et al. 2018)
Our assessment so far
- Provides an easy framework to write down distributed differentiable simulations and large scale Machine Learning tasks
- The Mesh TensorFlow project is still young, limited in scope, and with limited GPU parallelization support
$\Longrightarrow$ we need help from the Physics community to develop it for our needs!
Takeaway message
- We are combining physical and deep learning components to model
the Large-Scale Structure in a fast and differentiable way.
$\Longrightarrow$ This is a necessary backbone for large scale simulation-based inference. - We are demonstrating that large-scale simulations can be
implemented in distributed autodiff frameworks.
$\Longrightarrow$ We hope that this will one day become the norm.
Check out this blogpost to learn more
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html
![]()
True initial conditions
$z_0$
![]()
Reconstructed initial conditions $z$
![]()
Reconstructed dark matter distribution $x = f(z)$
![]()
Data
$x_{DM} = f(z_0)$
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html

True initial conditions
$z_0$

Reconstructed initial conditions $z$

Reconstructed dark matter distribution $x = f(z)$

Data
$x_{DM} = f(z_0)$
jax-cosmo: End-to-end automatically differentiable and GPU accelerated cosmology library
Collaborative project, join us :-)

A motivating example: Fisher forecasts
- Fisher matrices are notoriously unstable
$\Longrightarrow$ they rely on evaluating gradients by finite differences. - They do not scale well to large number of parameters.
- The main reason for using Fisher matrices is that full MCMCs are extremely slow, and get slower with dimensionality.

3D galaxy clustering with future wide-field surveys: Advantages of a spherical Fourier-Bessel analysis,
F. Lanusse, A. Rassat, J.L. Starck (2015)
How can we scale cosmological analyses to the hundreds of parameters of modern surveys ?
the hammer behind the Deep Learning revolution: Automatic Differentation
- Automatic differentiation allows you to compute analytic derivatives of arbitraty expressions:
If I form the expression $y = a * x + b$, it is separated in fundamental ops: $$ y = u + b \qquad u = a * x $$ then gradients can be obtained by the chain rule: $$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{ \partial u}{\partial x} = 1 \times a = a$$ - This is a fundamental tool in Machine Learning, and autodiff frameworks include TensorFlow and PyTorch.
Enters JAX: NumPy + Autograd + GPU
- JAX follows the NumPy api!
import jax.numpy as np - Arbitrary order derivatives
- Accelerated execution on GPU and TPU

jax-cosmo: Finally a differentiable cosmology library, and it's in JAX!

import jax.numpy as np
import jax_cosmo as jc
# Defining a Cosmology
cosmo = jc.Planck15()
# Define a redshift distribution with smail_nz(a, b, z0)
nz = jc.redshift.smail_nz(1., 2., 1.)
# Build a lensing tracer with a single redshift bin
probe = probes.WeakLensing([nz])
# Compute angular Cls for some ell
ell = np.logspace(0.1,3)
cls = angular_cl(cosmo_jax, ell, [probe])
Current main features
- Weak Lensing and Number counts probes
- Eisenstein & Hu (1998) power spectrum + halofit
- Angular $C_\ell$ under Limber approximation
$\Longrightarrow$ 3x2pt DES Y1 capable
let's compute a Fisher matrix
$$F = - \mathbb{E}_{p(x | \theta)}[ H_\theta(\log p(x| \theta)) ] $$
import jax
import jax.numpy as np
import jax_cosmo as jc
# .... define probes, and load a data vector
def gaussian_likelihood( theta ):
# Build the cosmology for given parameters
cosmo = jc.Planck15(Omega_c=theta[0], sigma8=theta[1])
# Compute mean and covariance
mu, cov = jc.angular_cl.gaussian_cl_covariance_and_mean(cosmo,
ell, probes)
# returns likelihood of data under model
return jc.likelihood.gaussian_likelihood(data, mu, cov)
# Fisher matrix in just one line:
F = - jax.hessian(gaussian_likelihood)(theta)
- No derivatives were harmed by finite differences in the computation of this Fisher!
- Only a small additional compute time compared to one forward evaluation of the model
Inference becomes fast and scalable
- Current cosmological MCMC chains take days, and typically require access to large computer clusters.
- Gradients of the log posterior are required for modern efficient and scalable inference techniques:
- Variational Inference
- Hamiltonian Monte-Carlo
- In jax-cosmo, we can trivially obtain exact gradients:
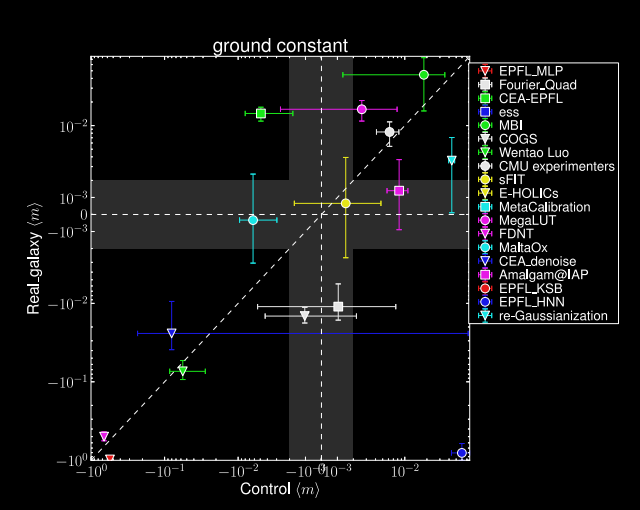
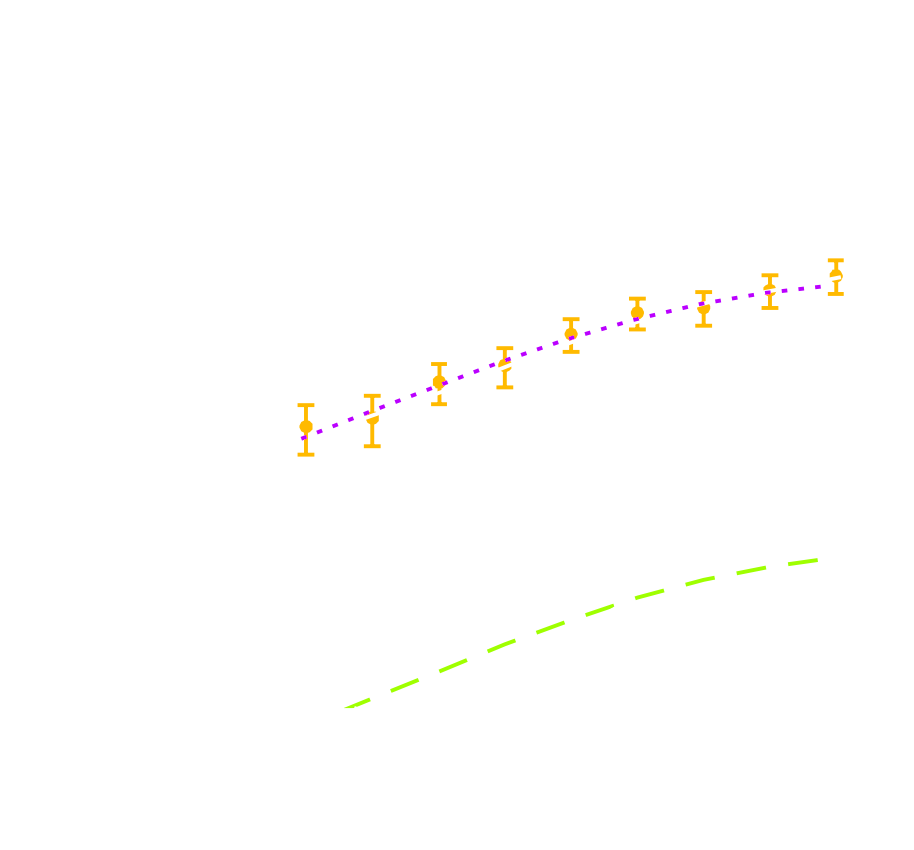
def log_posterior( theta ): return gaussian_likelihood( theta ) + log_prior(theta) score = jax.grad(log_posterior)(theta) - On a DES Y1 analysis, we find convergence in 70,000 samples with vanilla HMC, 140,000 with Metropolis-Hastings
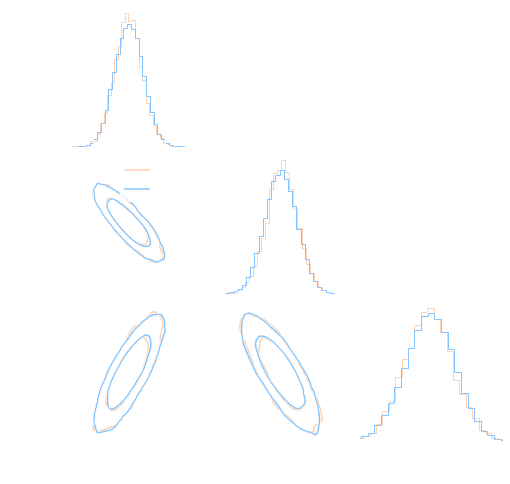
DES Y1 posterior, jax-cosmo HMC vs Cobaya MH
(credit: Joe Zuntz)
Takeaway message
- Automatic differentation has been a game changer for Machine Learning,
it can be for physics as well.
$\Longrightarrow$ Fast inference; instant and accurate forecasts; survey optimization; data compression; etc. - jax-cosmo proposes a numpy-like cosmology library in the intuitive and powerful JAX framework.
We need you!
Our goal is to build a high quality tool for the community
- Completely open and collaborative development on GitHub: https://github.com/DifferentiableUniverseInitiative/jax_cosmo
- Easily get in touch on Gitter for any questions https://gitter.im/DifferentiableUniverseInitiative/jax_cosmo
Conclusion
Conclusion
What can be gained by merging Deep Learning and Physical Models?
- Complement known physical models with data-driven components
- Learn galaxy morphologies from noisy and PSF-convolved data, for simulation purposes.
- Use data-driven model as prior for solving inverse problems such as deblending or deconvolution.
- Differentiable physical models for fast inference
- We are developing fast and distributed N-body simulations in TensorFlow.
- Even analytic cosmological computations can benefit from differentiability.
https://github.com/DifferentiableUniverseInitiative/jax_cosmo
Advertisement:
- Differentiable Universe Initiative (gitter.im/DifferentiableUniverseInitiative): Group of people interested in making everything differentiable! join the conversation :-)
Thank you !