Review and Perspective on
Deep Learning for the Analysis of Cosmological
Galaxy Surveys
François Lanusse
in collaboration with Marc Huertas-Company
slides at eiffl.github.io/talks/KEK2024
The Deep Learning Boom in Astrophysics
astro-ph abstracts mentioning Deep Learning,
CNN, or Neural Networks
Will AI Revolutionize the Scientific Analysis
of Cosmological
Surveys?
Review of the impact of Deep Learning in Galaxy Survey Science
https://ml4astro.github.io/dawes-review
outline of this talk
My goal for today: tour of Deep Learning applications relevant to cosmological physical inference.
- Interpreting Increasingly Complex Images
- Accelerating Numerical Simulations
- Simulation-Based Cosmological Inference
What has changed, what are the limitations, where is ML going next?
Interpreting Increasingly Complex Data
Dieleman+15, Huertas-Company+15, Aniyan+17, Charnock+17, Gieseke+17, Jacobs+17, Petrillo+17, Schawinski+17, Alhassan+18, Dominguez-Sanchez+18, George+18, Hinners+18, Lukic+18, Moss+18, Razzano+18, Schaefer+18, Allen+19, Burke+19, Carrasco-Davis+19, Chatterjee+19, Davies+19, Dominguez-Sanchez+19, Fusse+19, Glaser+19, Ishida+19, Jacobs+19, Katebi+19, Lanusse+19Liu+19, Lukic+19, Metcalf+19, Muthukrishna+19, Petrillo+19, Reiman+19, Boucaud+20, Chiani+20, Ghosh+20, Gomez+20, Hausen+20, Hlozek+20, Hosseinzadeh+20. Huang+20, Li+20, Moller+20, Paillassa+20, Tadaki+20, Vargas dos Santos+20, Walmsley+20, Wei+20, Allam+21, Arcelin+21, Becker+21, Bretonniere+21, Burhanudin+21, Davison+21, Donoso-Oliva+21, Jia+21, Lauritsen+21, Ono+21, Ruan+21, Sadegho+21, Tang+21, Tanoglidis+21, Vojtekova+21, Dhar+22Hausen+22, Orwat+22, Pimentel+22, Rezaei+22, Samudre+22, Shen+22, Walmsley+22
Credit: NAOJ
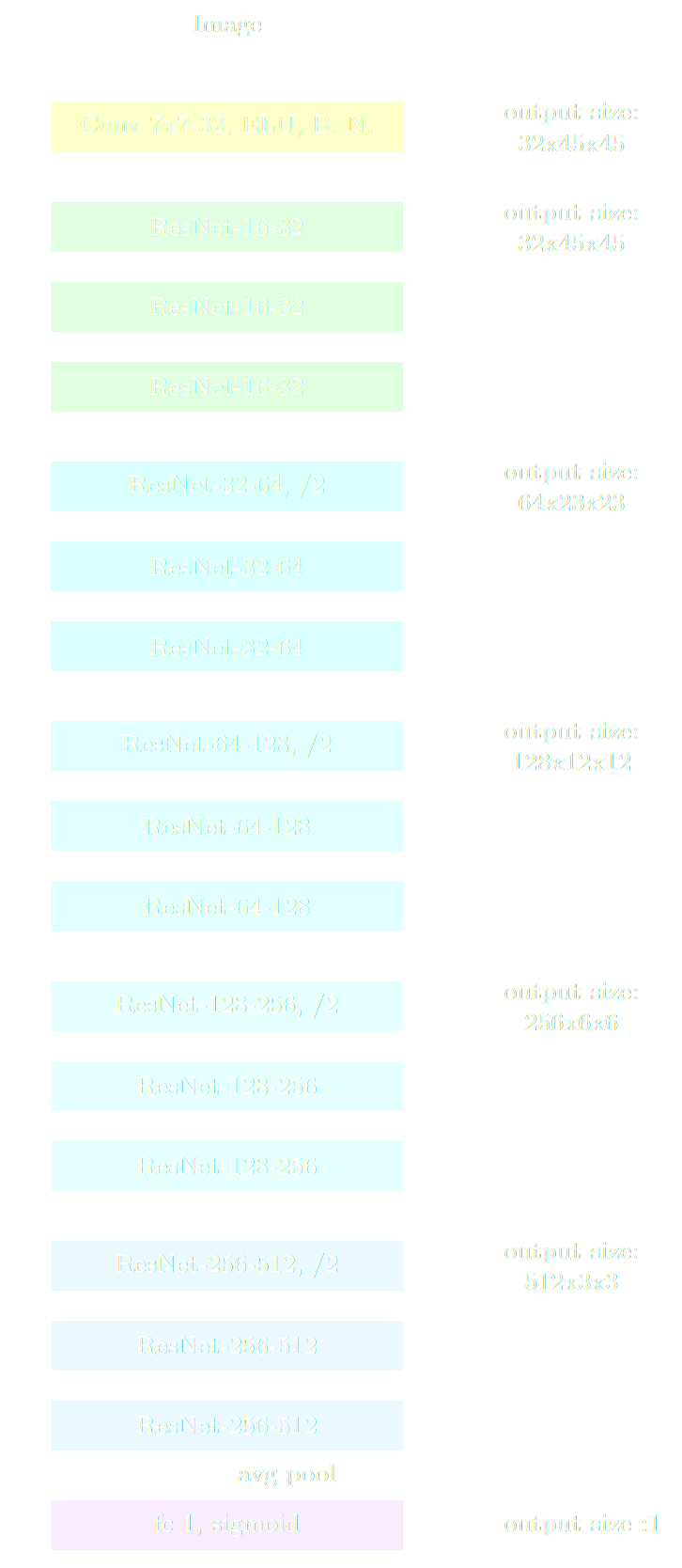
Detection and Classification of Astronomical Objects
Credit: NAOJ
A perfect task for Deep Learning!
Lanusse, Ma, Li, Collett, Li, Ravanbakhsh, Mandelbaum,
Poczos (2017)
Simulated gravitational lenses used for training
Better accuracy than human visual inspection!
Metcalf, et al. (2018)
Strong lens candidates in the DESI DECam Legacy Survey
Huang et al. (2019)
But this is not completely the end of the story...
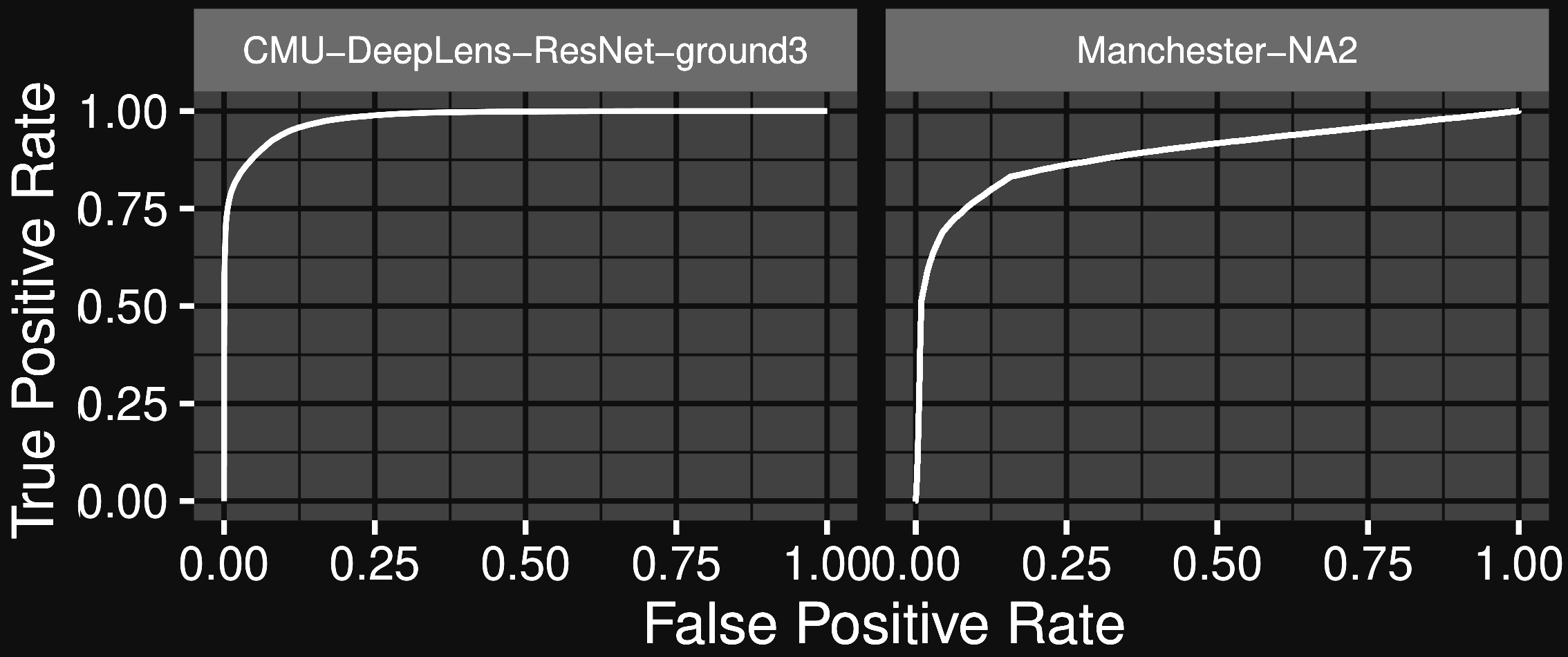
In total we have examined ∼ 50, 000 objects. On average one in 150 of the objects with [high] probability from the ResNet model is deemed a lens candidate through human inspection.
Huang et al. (2019)
$\Longrightarrow$ At the rate of LSST, this would mean needing human inspection for 20 million candidates.
Inference at the Image Level
Pasquet, Bertin, Treyer, Arnouts, Fouchez (2019)
Tucillo, Huertas-Company, et al. (2017)
Estimated Sersic index by CNN before adaptation (left),
after adaptation (right)
Inference at the Image Level
Reiman & Göhre (2018)
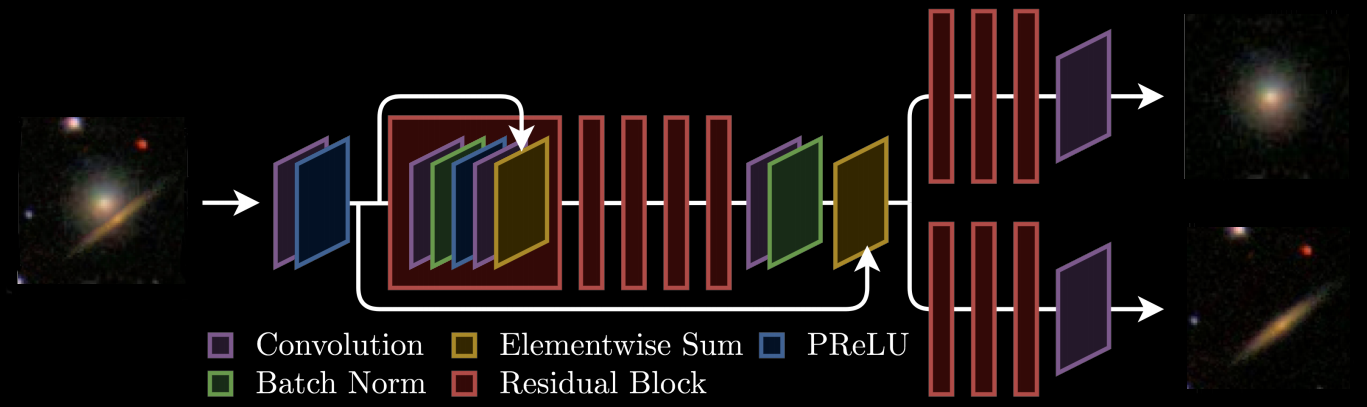
High Dimensional Bayesian Inverse Problems
Adam et al. (2022)
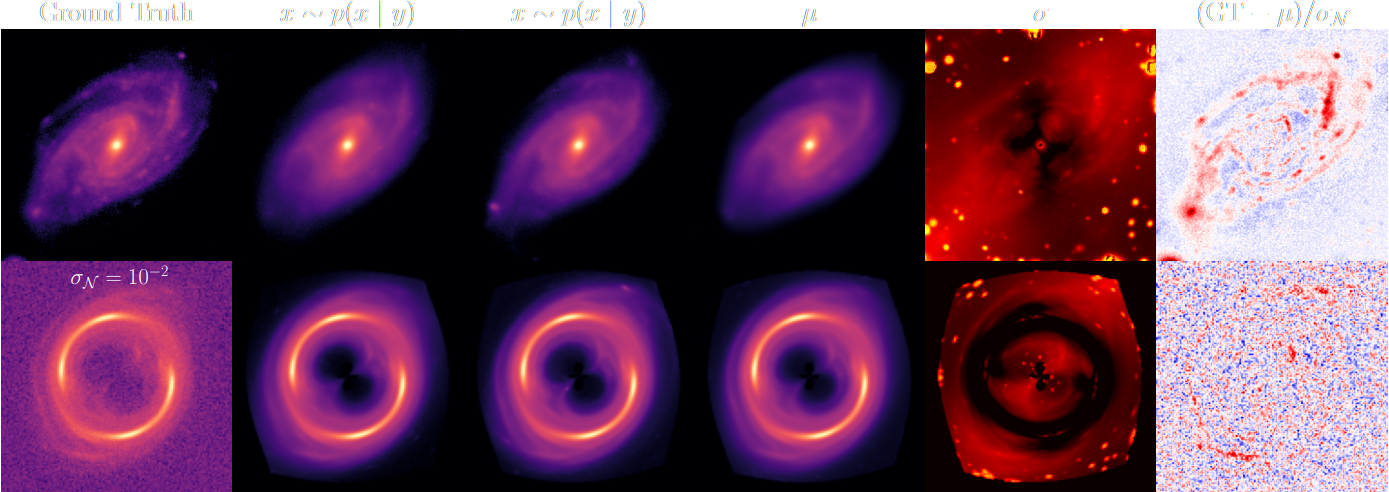
$\Longrightarrow$ generates samples from the full bayesian posterior
$$p(x | y) = \underbrace{p(y|x)}_{\mbox{known likelihood}} \qquad \underbrace{p(x)}_{\mbox{learned prior}}$$
takeways
Is Deep Learning Really Changing the Game in Interpreting Survey
Data?
-
For Detection, Classification, Cleaning tasks:
Yes, within limits
$\Longrightarrow$ As long as we don't need to understand precisely the model response/selection function. -
For infering physical properties needed in downstream
analysis: Not really...
- In general the exact response is not known, and very non-linear.
- Not addressing the core question of representativeness of training data.
- For solving challenging data restoration problems: getting there!
- Still need to be careful about the representativeness of training data.
- But the problem is well defined, likelihood is physically motivated, and the response is well understood.
Accelerating Cosmological Simulations with Deep Learning
Rodriguez+19, Modi+18, Berger+18, He+18, Zhang+19, Troster+19, Zamudio- Fernandez+19, Perraudin+19, Charnock+19, List+19, Giusarma+19, Bernardini+19, Chardin+19, Mustafa+19, Ramanah+20, Tamosiunas+20, Feder+20, Moster+20, Thiele+20, Wadekar+20, Dai+20, Li+20, Lucie-Smith+20, Kasmanoff+20, Ni+21, Rouhiainen+21, Harrington+21, Horowitz+21, Horowitz+21, Bernardini+21, Schaurecker+21, Etezad-Razavi+21, Curtis+21
AI-assisted superresolution cosmological simulations
Li, Ni, Croft, Di Matteo, Bird, Feng (2021)
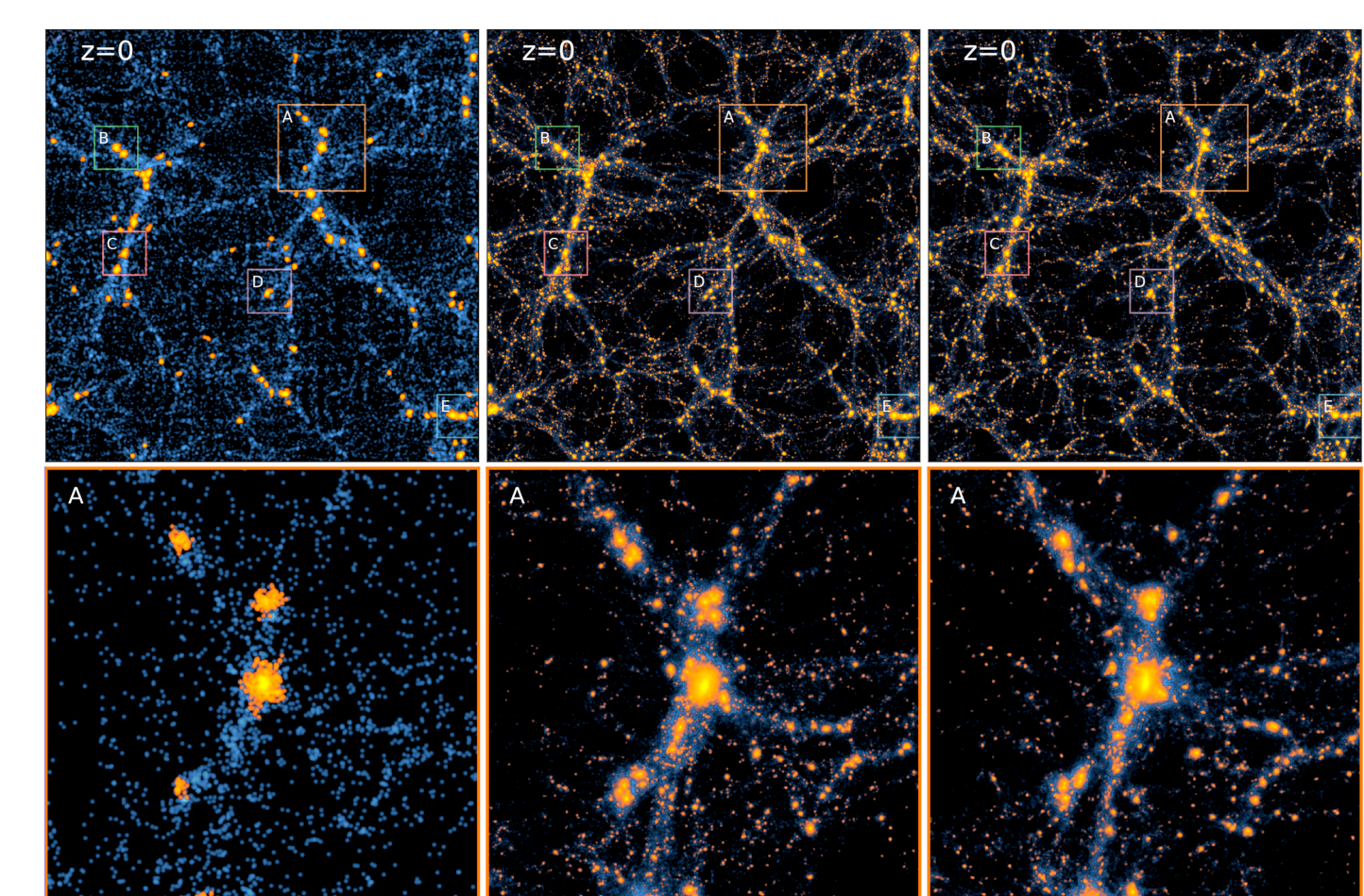
x8 super-resolution
- Inputs low resolution particle displacement field, outputs samples from a distribution $p_\theta(x_{SR} | x_{LR})$
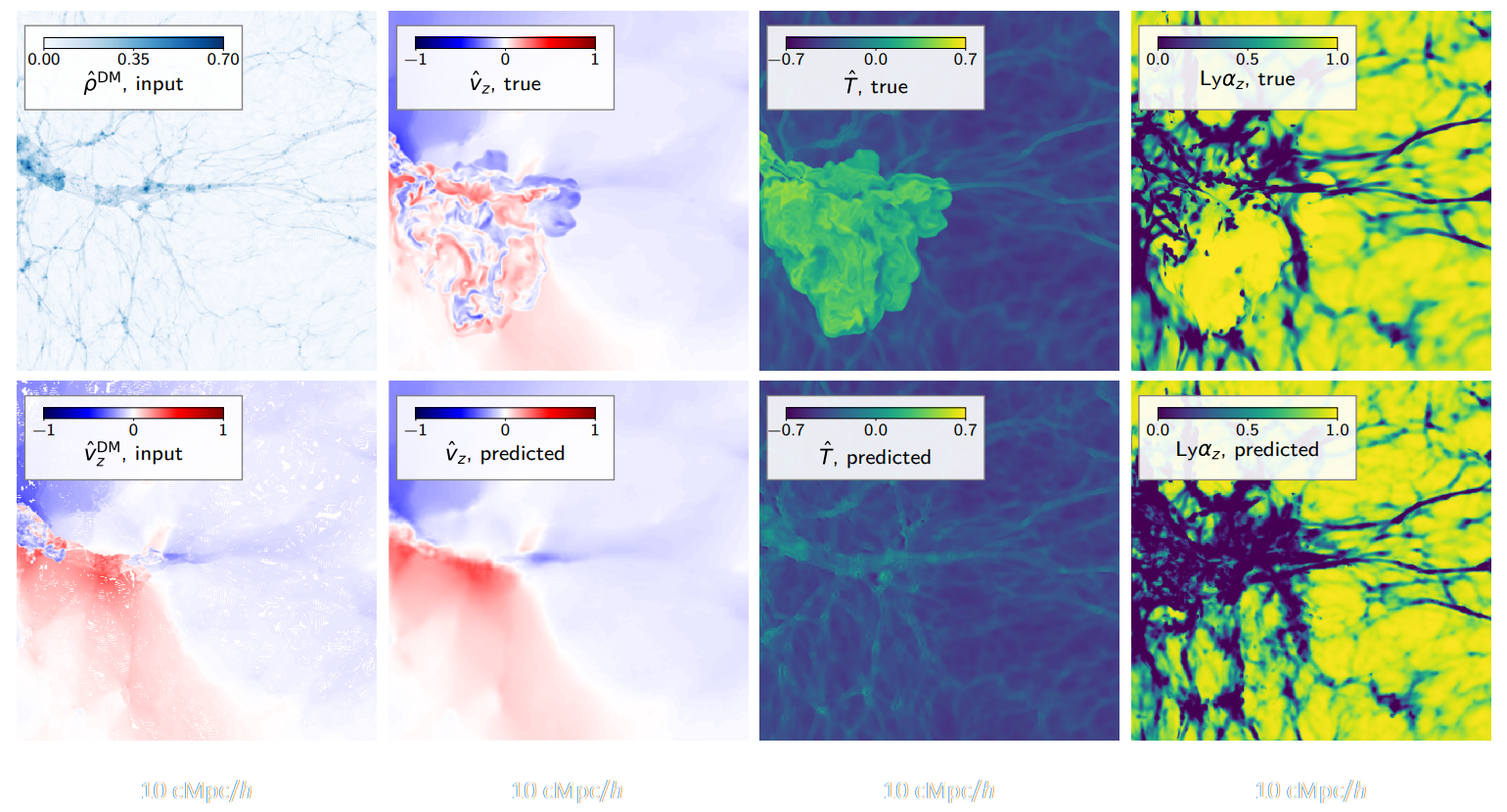
Fast, high-fidelity Lyman α forests with CNNs
Harrington, Mustafa, Dornfest, Horowitz, Lukić (2021)
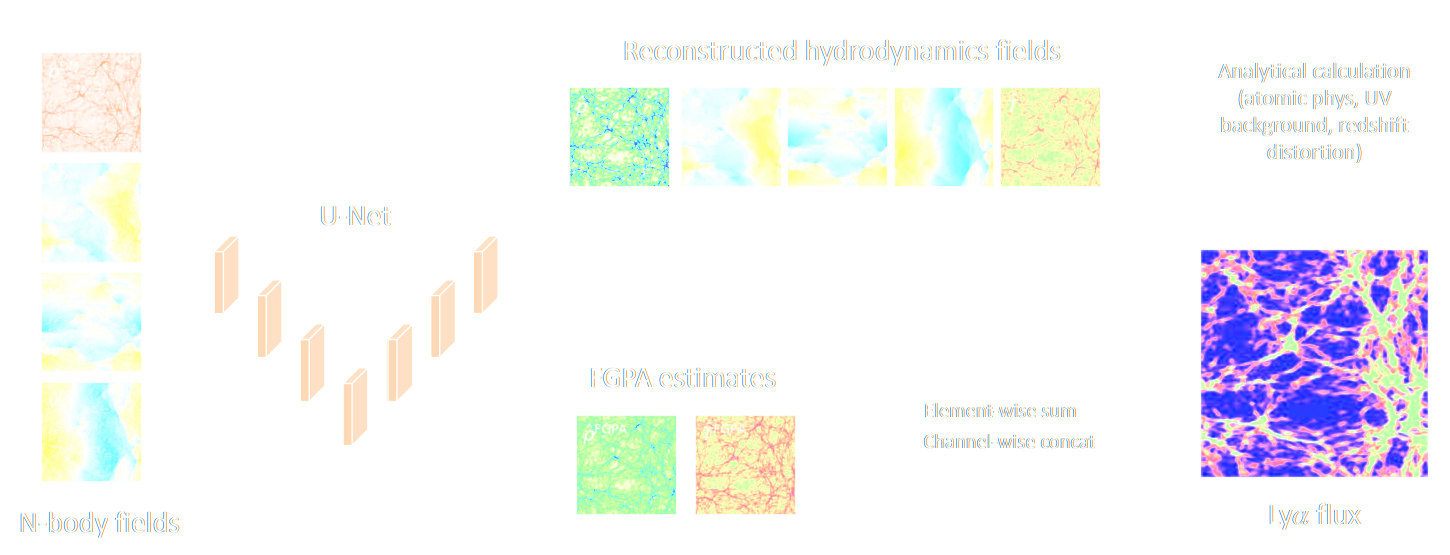
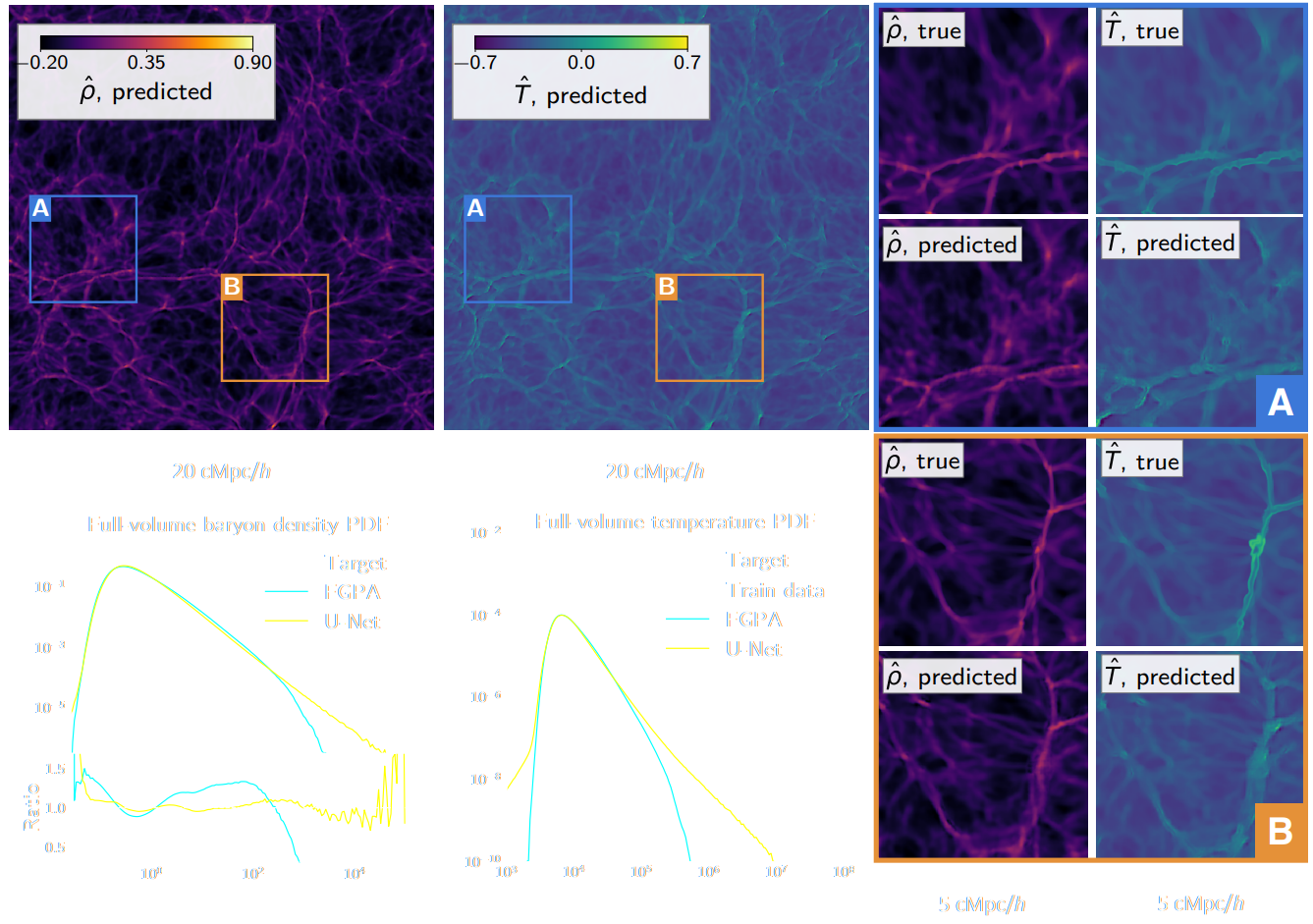
are these Deep Learning models a real game-changer?
The Limitations of Black-Box Large Deep Learning Approaches
-
There is a risk that a large Deep Learning model can
silently fail.
$\Rightarrow$ How can we build confidence in the output of the neural network? -
Training these models can require a very large number of
simulations.
$\Rightarrow$ Do they bring a net computational benefit?- In case of the super-resolution model of Li et al. (2021), only 16 full-resolution $512^3$ N-body were necessary.
-
In many cases, the accuracy (not the quantity) of
simulations will be the main bottleneck.
$\Rightarrow$ What new science are these deep learning models enabling?- In the case of cosmological SBI, they do not help us resolve the uncertainty on the simulation model.
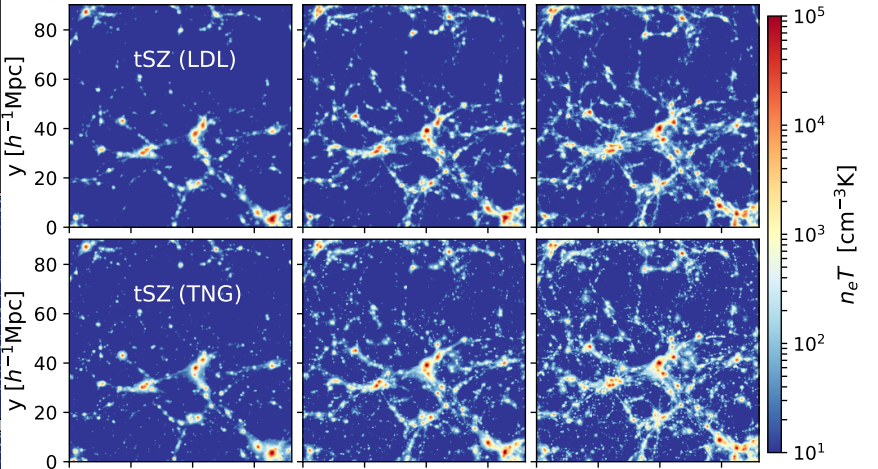
(Harrington et al. 2021)
What Would be Desirable Properties of robust ML-based Emulation
Methods?
- Make use of known symmetries and physical constraints.
- Modeling residuals to an approximate physical model
-
Minimally parametric
- Can be trained with a very small number of simulations
- Could potentially be inferred from data!
Learning effective physical laws for generating cosmological hydrodynamics with Lagrangian Deep Learning
Dai & Seljak (2021)
-
The Lagrangian Deep Learning approach:
- Run an approximate Particle-Mesh DM simulation (about 10 steps)
-
Introduce a displacement $\mathbf{S}$ of particles:
\begin{equation} \mathbf{S}=-\alpha\nabla \hat{O}_{G}
f(\delta) \end{equation} where $\hat{O}_{g}$ is a
parametric Fourier-space filter, $f$ is a parametric
function of $\delta$.
$\Rightarrow$ Respects translational and rotational symmetries. - Apply a non-linear function on the resulting density field $\delta^\prime$: $$F(x) = \mathrm{ReLu}(b_1 f(\delta^\prime) - b_0)$$
$\Longrightarrow$ Only need to fit ~10 parameters to
reproduce a desired field from an hydrodynamical field.
takeaways
- Deep Learning may allow us to scale up existing simulation suites (with caveats), but it is not replacing simulation codes.
- One exciting prospect rarely explored so far in astrophysics is using Deep Learning to accelerate the N-body/hydro solver.
https://sites.google.com/view/meshgraphnets
(Pfaff et al. 2021)
Simulation-Based Cosmological Inference
Ravanbakhsh+17, Brehmer+19, Ribli+19, Pan+19, Ntampaka+19, Alexander+20, Arjona+20, Coogan+20, Escamilla- Rivera+20, Hortua+20, Vama+20, Vernardos+20, Wang+20, Mao+20, Arico+20, Villaescusa_navarro+20, Singh+20, Park+21, Modi+21, Villaescusa-Navarro+21ab, Moriwaki+21, DeRose+21, Makinen+21, Villaescusa-Navaroo+22
the limits of traditional cosmological inference
HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
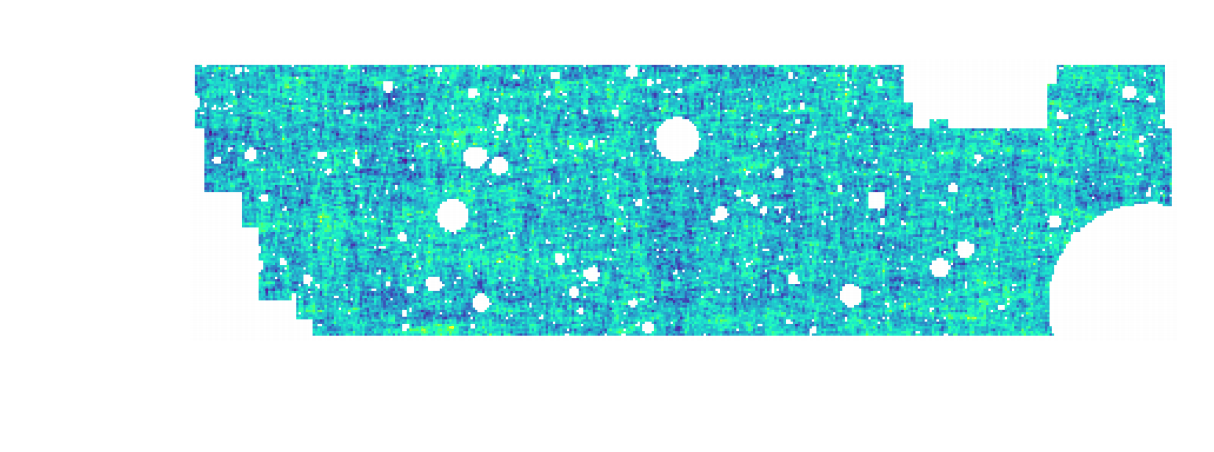
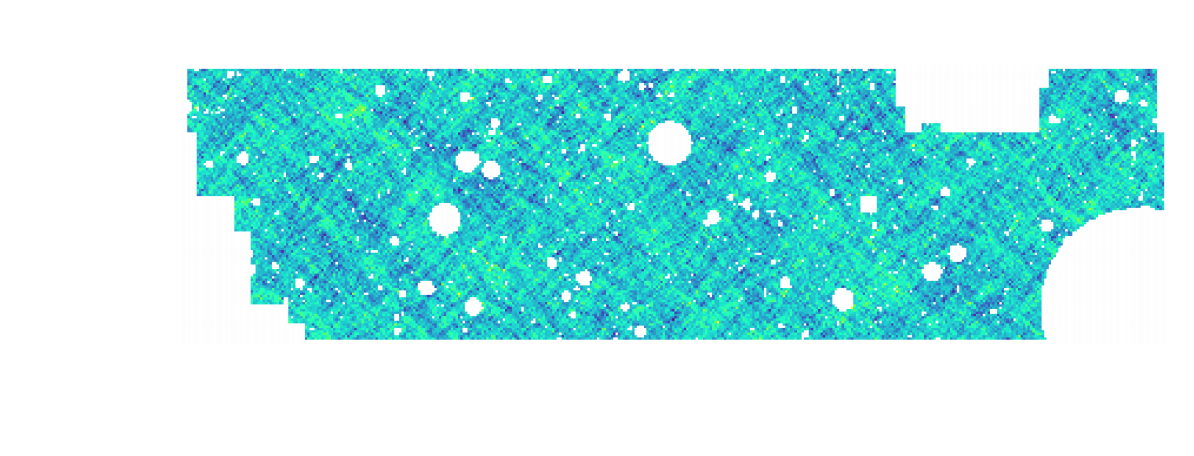
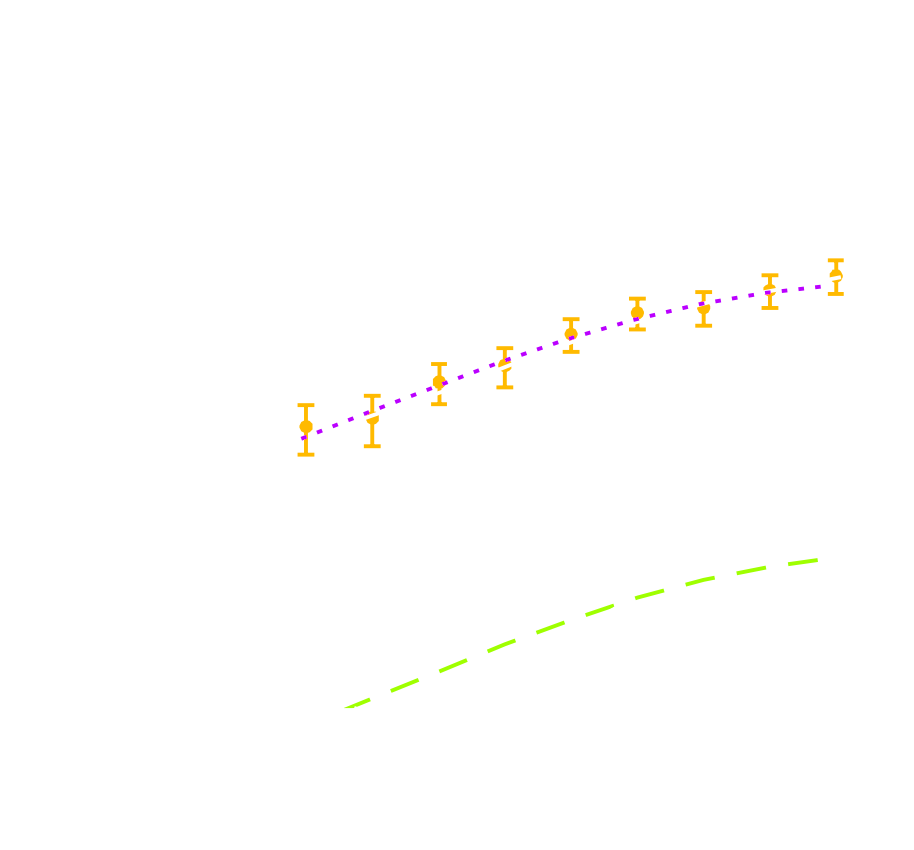
(Hikage et al. 2018)
-
Measure the ellipticity $\epsilon = \epsilon_i + \gamma$ of
all galaxies
$\Longrightarrow$ Noisy tracer of the weak lensing shear $\gamma$ -
Compute summary statistics based on 2pt
functions,
e.g. the power spectrum - Run an MCMC to recover a posterior on model parameters, using an analytic likelihood $$ p(\theta | x ) \propto \underbrace{p(x | \theta)}_{\mathrm{likelihood}} \ \underbrace{p(\theta)}_{\mathrm{prior}}$$
Main limitation: the need for an explicit likelihood
We can only compute the likelihood for
simple summary statistics and on
large scales
$\Longrightarrow$ We are dismissing a significant fraction of
the information!
Full-Field Simulation-Based Inference
- Instead of trying to analytically evaluate the likelihood of
sub-optimal summary statistics, let us build a forward model of the full observables.
$\Longrightarrow$ The simulator becomes the physical model. - Each component of the model is now tractable, but at the cost of a large number of latent variables.
Benefits of a forward modeling approach
- Fully exploits the information content of the data (aka "full field inference").
- Easy to incorporate systematic effects.
- Easy to combine multiple cosmological probes by joint simulations.
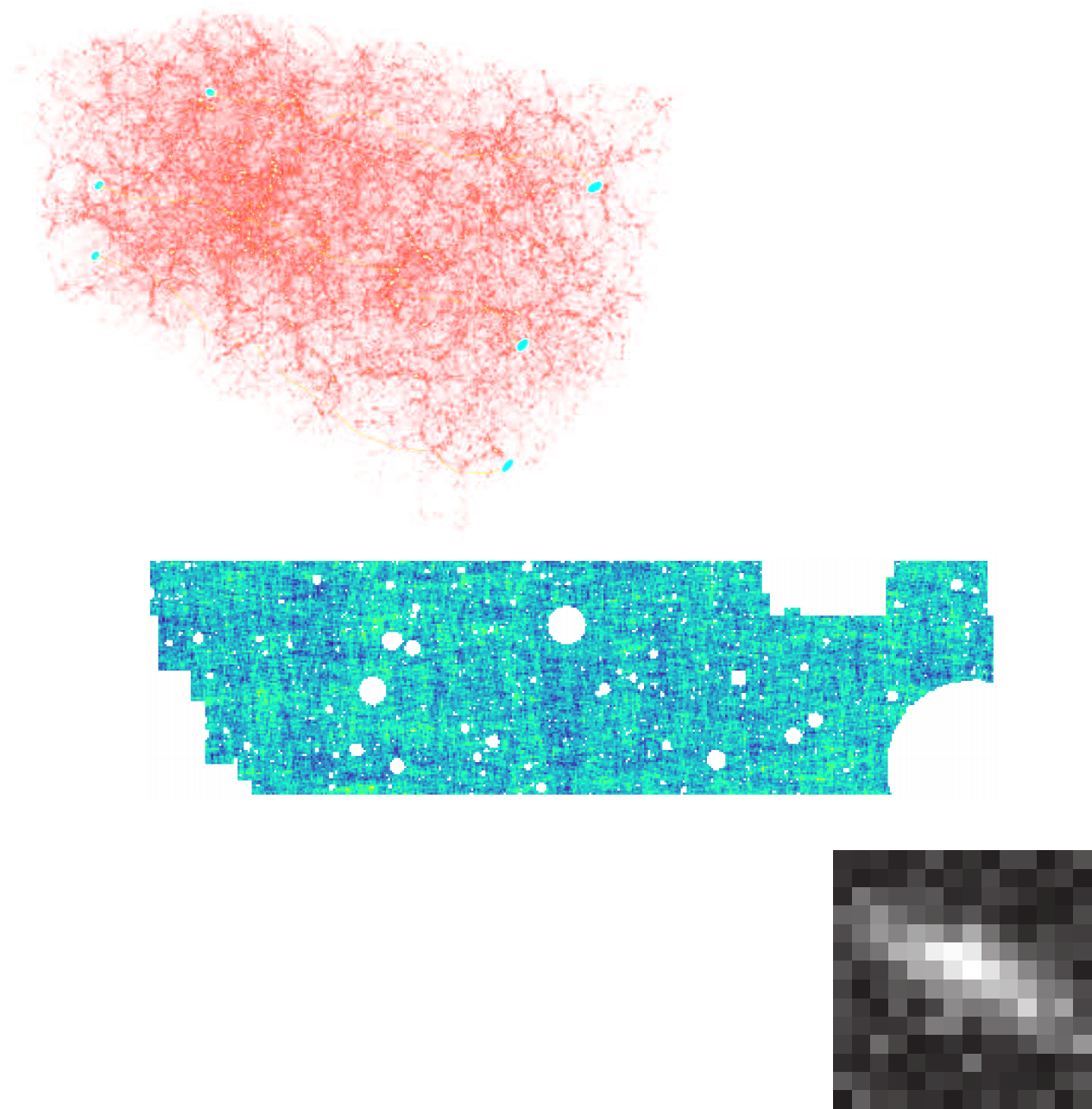
(Porqueres et al. 2021)
...so why is this not mainstream?
The Challenge of Simulation-Based Inference
$$ p(x|\theta) = \int p(x, z | \theta) dz = \int p(x | z,
\theta) p(z | \theta) dz $$ Where $z$ are
stochastic latent variables of the simulator.
$\Longrightarrow$ This marginal likelihood is intractable! Hence the phrase "Likelihood-Free Inference"
$\Longrightarrow$ This marginal likelihood is intractable! Hence the phrase "Likelihood-Free Inference"
Black-box Simulators Define Implicit Distributions
- A black-box simulator defines $p(x | \theta)$ as an implicit distribution, you can sample from it but you cannot evaluate it.
- This gives us a procedure to sample from the Bayesian joint distribution $p(x, \theta)$: $$(x, \theta) \sim p(x | \theta) \ p(\theta)$$
- Key Idea: Use a parametric distribution model $\mathbb{P}_\varphi$ to approximate an implicit distribution.
- Neural Likelihood Estimation: $\mathcal{L} = - \mathbb{E}_{(x,\theta)}\left[ \log p_\varphi( x | \theta ) \right] $
- Neural Posterior Estimation: $\mathcal{L} = - \mathbb{E}_{(x,\theta)}\left[ \log p_\varphi( \theta | x ) \right] $
- Neural Ratio Estimation: $\mathcal{L} = - \mathbb{E}_{\begin{matrix} (x,\theta)~p(x,\theta) \\ \ \theta^\prime \sim p(\theta) \end{matrix}} \left[ \log r_\varphi(x,\theta) + \log(1 - r_\varphi(x, \theta^\prime)) \right] $
A variety of algorithms
Lueckmann, Boelts, Greenberg, Gonçalves, Macke (2021)
A few important points:
- Amortized inference methods, which estimate $p(\theta | x)$, can greatly speed up posterior estimation once trained.
- Sequential Neural Posterior/Likelihood Estimation methods can actively sample simulations needed to refine the inference.
A Practical Recipe for Careful Simulation-Based Inference
Estimating conditional densities
in high dimensions is hard...
To be more robust, you can decompose the problem into two tasks:
- Step I - Dimensionality Reduction: Compress your observables $x$ to a low dimensional summary statistic $y$
![]()
- Step II - Conditional Density Estimation: Estimate the posterior $p(\theta | y)$ using SBI from the low dimensional summary statistic $y$.
Automated Neural Summarization
- Introduce a parametric function $f_\varphi$ to reduce the dimensionality of the data while preserving information.
Information point of view
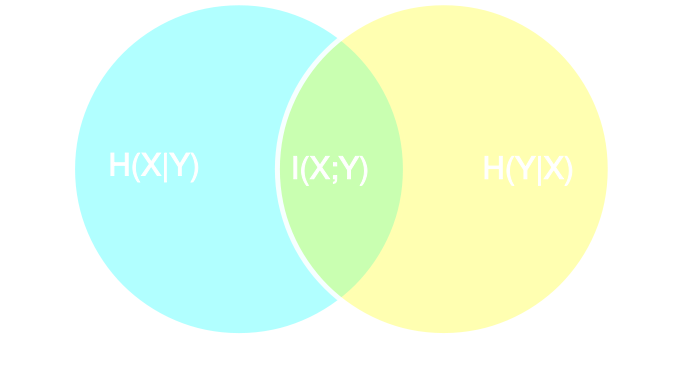
- Summary statistics $y$ is sufficient for $\theta$ if $$ I(Y; \Theta) = I(X; \Theta) \Leftrightarrow p(\theta | x ) = p(\theta | y) $$
- Variational Mutual Information Maximization
$$ \mathcal{L} \ = \ \mathbb{E}_{x, \theta} [ \log q_\phi(\theta | y=f_\varphi(x)) ] \leq I(Y; \Theta) $$
(Barber & Agakov variational lower bound)
Jeffrey, Alsing, Lanusse (2021)
Another Approach: maximizing the Fisher information
Information Maximization Neural Network (IMNN)
$$\mathcal{L} \ = \ - | \det \mathbf{F} | \ \mbox{with} \ \mathbf{F}_{\alpha, \beta} = tr[ \mu_{\alpha}^t C^{-1} \mu_{\beta} ] $$
Charnock, Lavaux, Wandelt (2018) 
Can we just retire all conventional likelihood-based analyses?
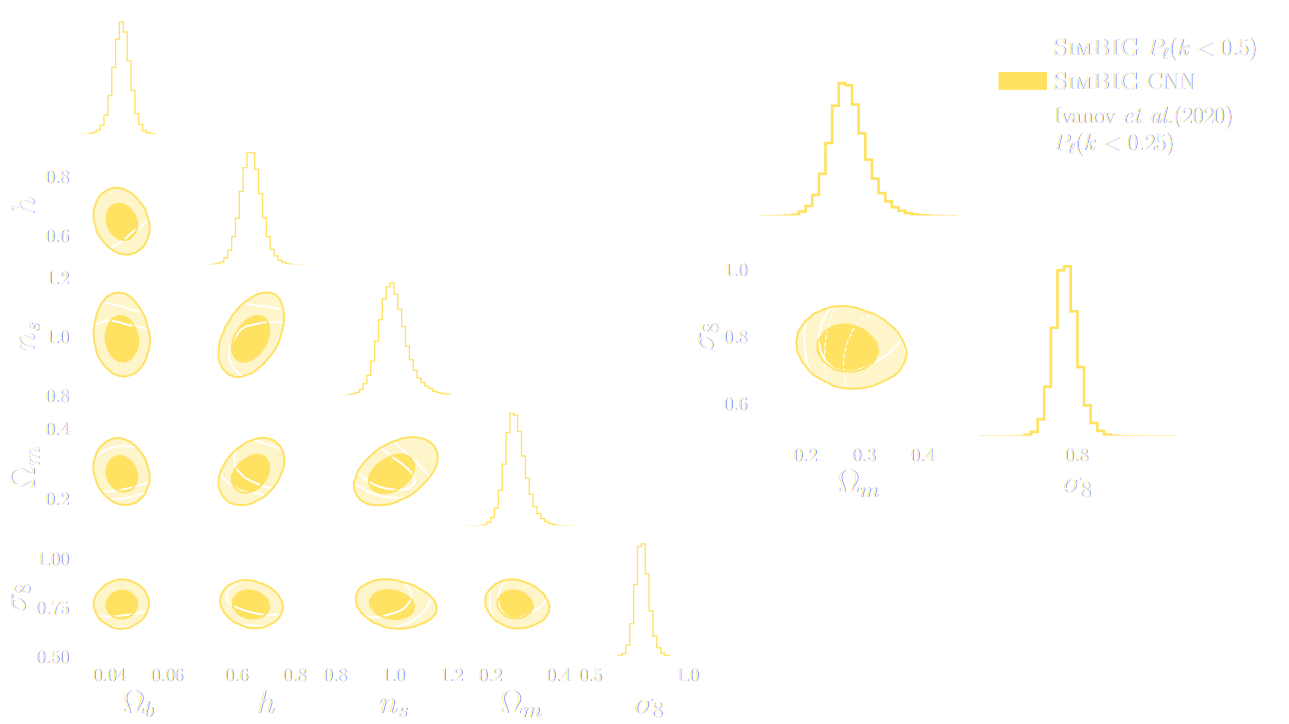
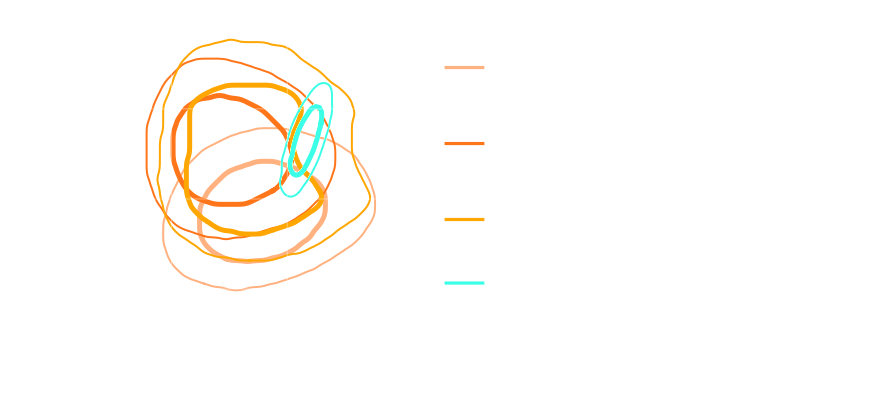
SIMBIG: Field-level SBI of Large Scale Structure (Lemos et al. 2023)
BOSS CMASS galaxy sample: Data vs Simulations
- 20,000 simulated galaxy samples at 2,000 cosmologies
Hahn et al. (2022)
$w$CDM analysis of KiDS-1000 Weak Lensing (Fluri et al. 2022)
Kacprzak, Fluri, Schneider, Refregier, Stadel (2022)
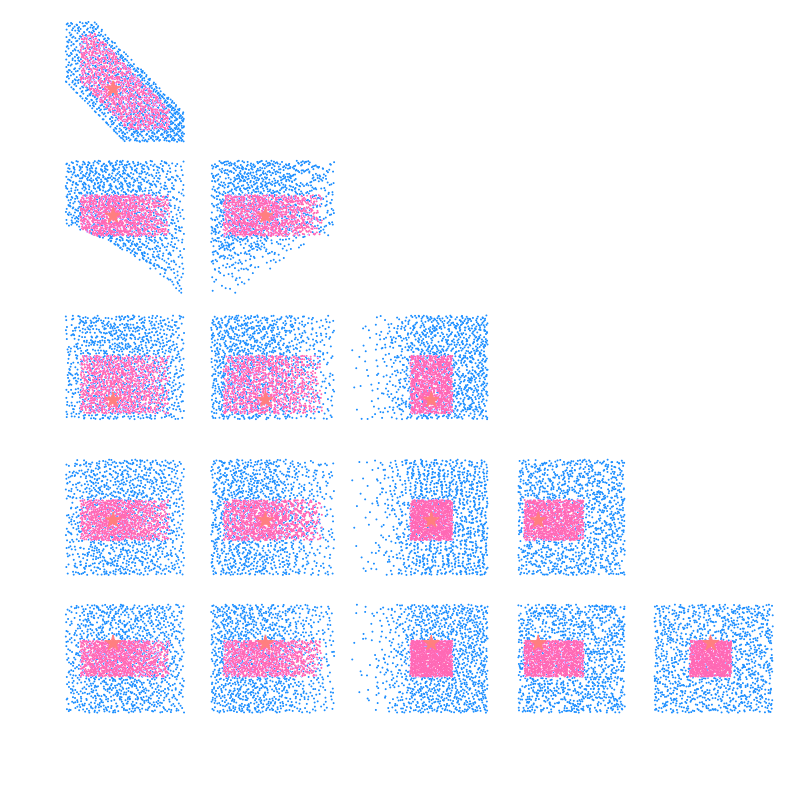
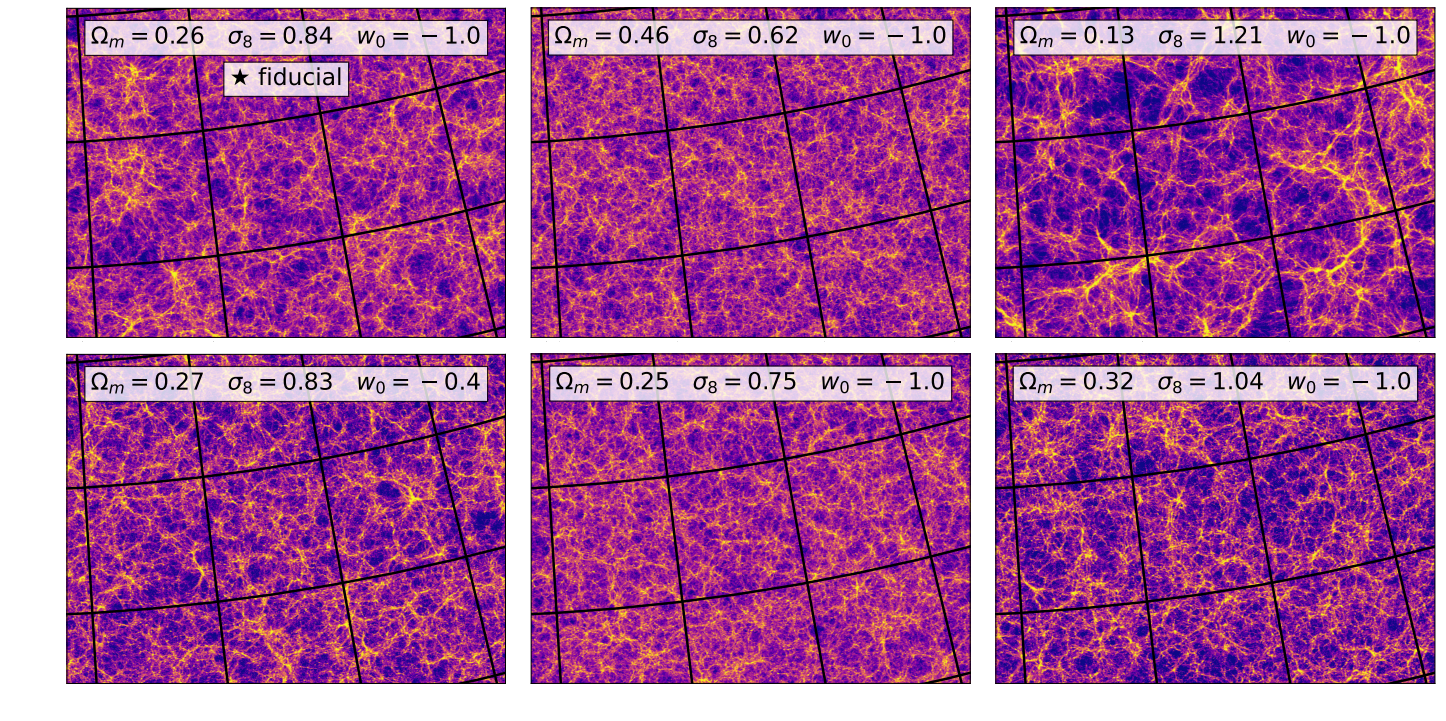
CosmoGridV1 simulations, available at http://www.cosmogrid.ai
- 17,500 simulations at 2,500 cosmologies
- Lensing, Intrinsic Alignment, and Galaxy Density
maps at nside=512
Fluri, Kacprzak, Lucchi, Schneider, Refregier, Hofmann (2022)
KiDS-1000 footprint and simulated data
![]()
- Neural Compressor: Graph Convolutional Neural Network on the Sphere
Trained by Fisher information maximization.
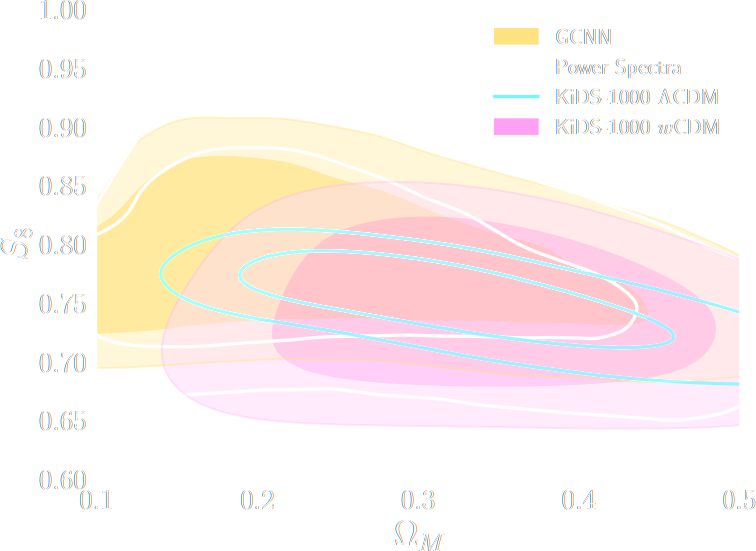
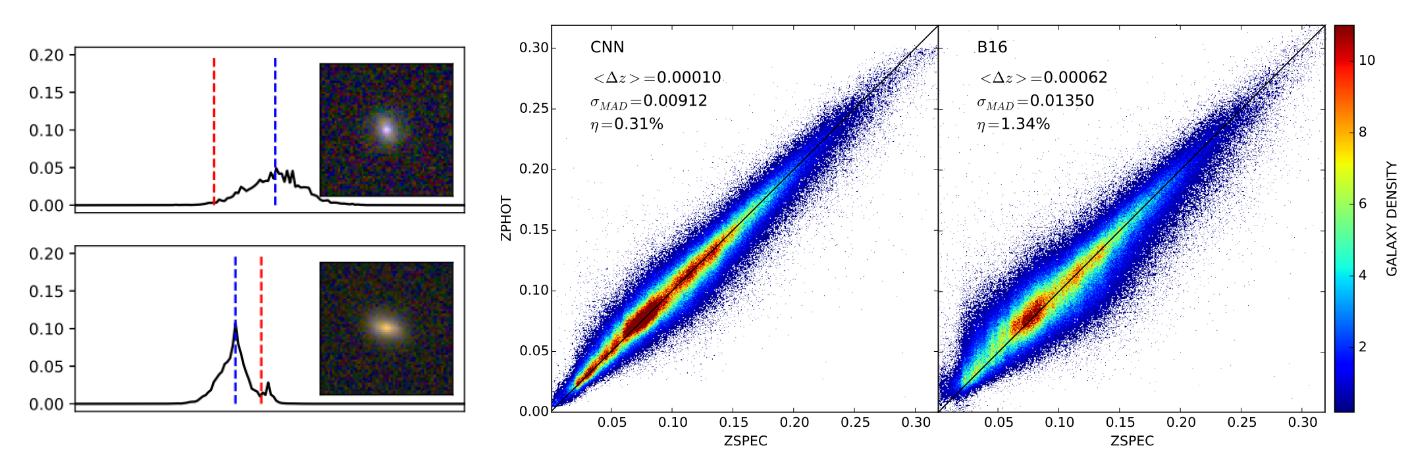
Cosmological constraints from HSC survey first-year data using deep learning
Lu, Haiman, Li (2023)
How much usable information is there beyond the power spectrum?
Chisari et al. (2018)
Ratio of power spectrum in hydrodynamical simulations vs. N-body simulations
Secco et al. (2021)
DES Y3 Cosmic Shear data vector
$\Longrightarrow$ Can we find non-Gaussian information that is not affected by baryons?
Example of unforeseen impact of shortcuts in simulations
Gatti, Jeffrey, Whiteway et al. (2023)
Is it ok to distribute lensing source galaxies randomly in simulations, or should they be clustered?
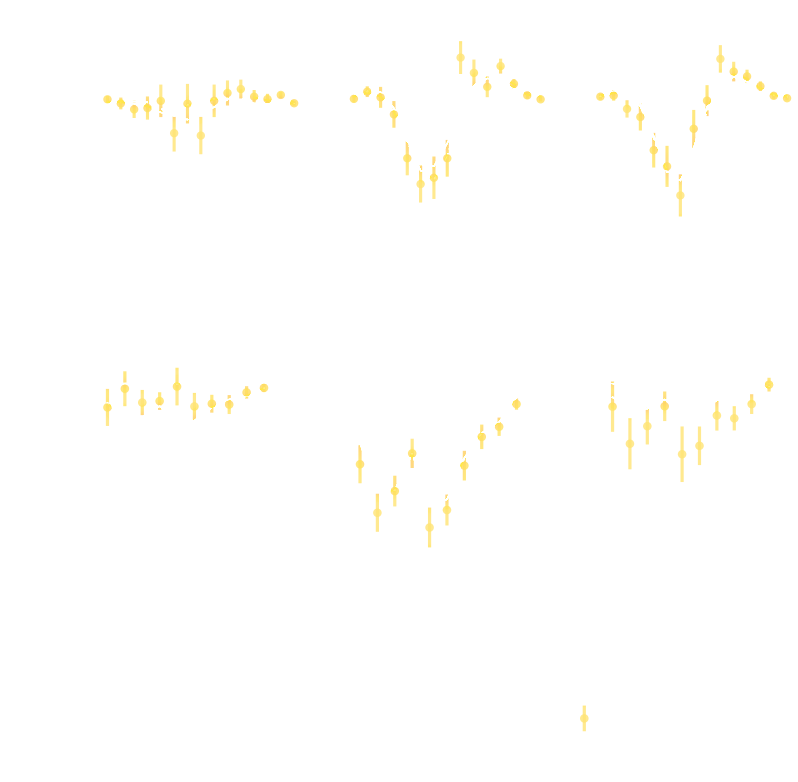
$\Longrightarrow$ An SBI analysis could be biased by this effect and you would never know it!
takeways
-
Likelihood-Free Inference automatizes inference over
numerical simulators.
- Turns both summary extraction and inference problems into an optimization problems
- Deep learning allows us to solve that problem!
-
In the context of upcoming surveys, this techniques provides
many advantages:
- Amortized inference: near instantaneous parameter inference, extremely useful for time-domain.
- Optimal information extraction: no longer need for restrictive modeling assumptions needed to obtain tractable likelihoods.
Will we be able to exploit all of the information content of LSST,
Euclid, DESI?
$\Longrightarrow$ Not rightaway, but it is not the fault of Deep
Learning!
- Deep Learning has redefined the limits of our statistical tools, creating additional demand on the accuracy of simulations far beyond the power spectrum.
- Neural compression methods have the downside of being opaque. It is much harder to detect unknown systematics.
- We will need a significant number of large volume, high resolution simulations.
Conclusion
Deep Learning 8 years later: Revolution or Incremental Science?
- The most impactful applications so far are low level “out-of-the-box” data reduction applications (incremental science).
- In some ways, the statistical tools are now beyond our physical modeling capabilities, they are no longer a limiting factor.
- Foundation Models for feature extraction:
- More information can be extracted from data by self-supervised learning across surveys and data modalities
- Generative Models for Data-Driven modeling:
- Generative models can be used to learn part of the physical processes that generate the data.
Where are we going next?
Will Foundation Models make their way to astrophysics?
Thank you !