Merging deep learning with physical models
for the analysis of modern cosmological surveys
François Lanusse



slides at eiffl.github.io/talks/IAIFI2023
the $\Lambda$CDM view of the Universe



the Rubin Observatory Legacy Survey of Space and Time
- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed $\sim1000$ times
Previous generation survey: SDSS
Image credit: Peter Melchior
Current generation survey: DES
Image credit: Peter Melchior
LSST precursor survey: HSC
Image credit: Peter Melchior
We need to rethink all stages of data analysis for modern surveys

Bosch et al. 2017
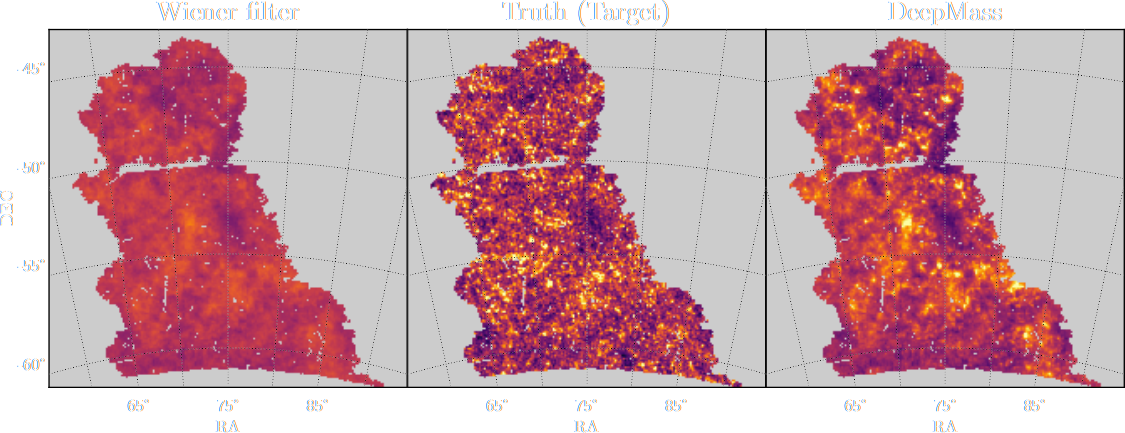
Jeffrey, Lanusse, et al. 2020
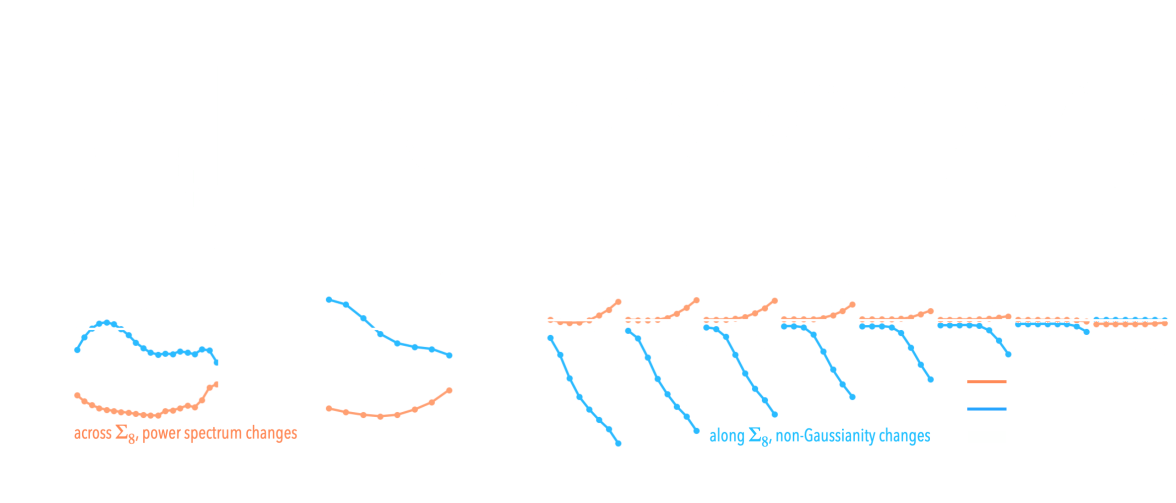
Cheng et al. 2020
- Galaxies are no longer blobs.
- Signals are no longer Gaussian.
- Cosmological likelihoods are no longer tractable.
$\Longrightarrow$ This is the end of the analytic era...
... but the beginning of the data-driven era
Case I: Examples from data, no accurate physical model
![]()

Mandelbaum et al. 2014
Case II: Physical model only available as a simulator
![]()

Osato et al. 2020
$\Longrightarrow$ Examples of implicit distributions: we have access to samples $\{x_0, x_1, \ldots, x_n \}$
but we cannot evaluate $p(x)$.
How can we leverage implicit distributions
for physical Bayesian inference?
The answer is: Deep Generative Modeling
- The goal of generative modeling is to learn an implicit distribution $\mathbb{P}$ from which the training set $X = \{x_0, x_1, \ldots, x_n \}$ is drawn.
- Usually, this means building a parametric model $\mathbb{P}_\theta$ that tries to be close to $\mathbb{P}$.

True $\mathbb{P}$

Samples $x_i \sim \mathbb{P}$

Model $\mathbb{P}_\theta$
- Once trained, you can typically sample from $\mathbb{P}_\theta$ and/or evaluate the likelihood $p_\theta(x)$.
Why isn't it easy?
- The curse of dimensionality put all points far apart in high dimension


Distance between pairs of points drawn from a Gaussian distribution.
- Classical methods for estimating probability densities, i.e. Kernel Density Estimation (KDE) start to fail in high dimension because of all the gaps
The evolution of generative models





- Deep Belief Network
(Hinton et al. 2006) - Variational AutoEncoder
(Kingma & Welling 2014) - Generative Adversarial Network
(Goodfellow et al. 2014) - Wasserstein GAN
(Arjovsky et al. 2017) - Midjourney v5 Guided Latent Diffusion (2023)
$\Longrightarrow$ We can consider the problem of learning
distributions to be essentially solved even in high dimensions.
Focus of this talk
This talk
Generic approach to uncertainty quantification and interpretability:
- (Differentiable) Physical Forward Models
- Deep Generative Models
- Bayesian Inference
Solving Inverse Problems
with deep implicit priors
Branched GAN model for deblending (Reiman & Göhre, 2018)
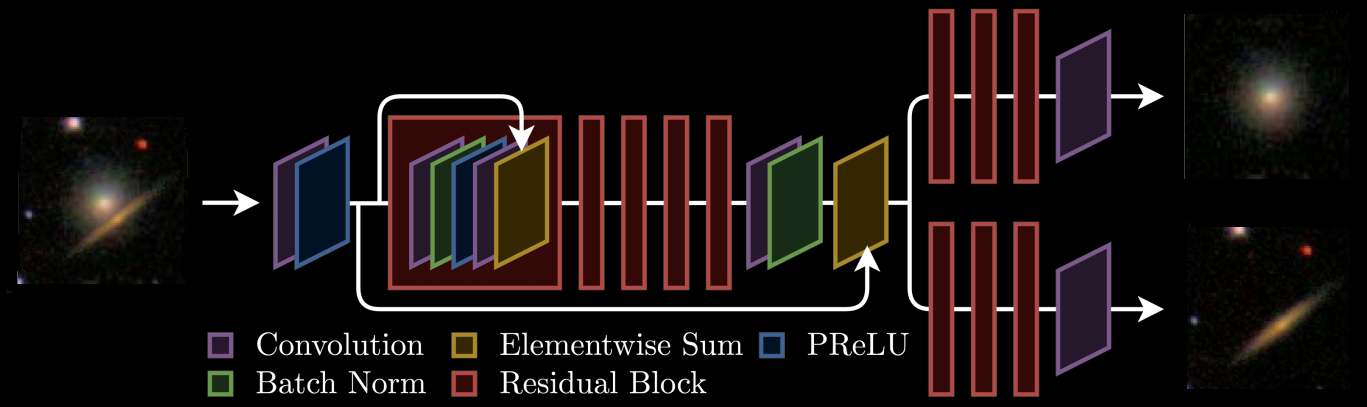
The issue with using deep learning as a black-box
- No explicit control of noise, PSF, number of sources.
- Model would have to be retrained for all observing configurations
- No guarantees on the network output (e.g. flux preservation, artifacts)
- No proper uncertainty quantification.

Linear inverse problems
$\boxed{y = \mathbf{A}x + n}$$\mathbf{A}$ is known and encodes our physical understanding of the problem.
$\Longrightarrow$ When non-invertible or ill-conditioned, the inverse problem is ill-posed with no unique solution $x$
 Deconvolution
Deconvolution
 Inpainting
Inpainting
 Denoising
Denoising
What Would a Bayesian Do?
$\boxed{y = \mathbf{A}x + n}$The Bayesian view of the problem:
$$ p(x | y) \propto p(y | x) \ p(x) $$
- $p(y | x)$ is the data likelihood, which contains the physics
- $p(x)$ is the prior knowledge on the solution.
- With these concepts in hand we can:
- Estimate for instance the Maximum A Posteriori solution:
$$\hat{x} = \arg\max\limits_x \ \log p(y \ | \ x) + \log p(x)$$ - Estimate from the full posterior p(x|y) with MCMC or Variational Inference methods.
How do you choose the prior ?
Classical examples of signal priors
Sparse
![]()
$$ \log p(x) = \parallel \mathbf{W} x \parallel_1 $$
$$ \log p(x) = \parallel \mathbf{W} x \parallel_1 $$
Gaussian
![]() $$ \log p(x) = x^t \mathbf{\Sigma^{-1}} x $$
$$ \log p(x) = x^t \mathbf{\Sigma^{-1}} x $$
 $$ \log p(x) = x^t \mathbf{\Sigma^{-1}} x $$
$$ \log p(x) = x^t \mathbf{\Sigma^{-1}} x $$
Total Variation
![]() $$ \log p(x) = \parallel \nabla x \parallel_1 $$
$$ \log p(x) = \parallel \nabla x \parallel_1 $$
But what about this?
Getting started with Deep Priors: deep denoising example
$$ \boxed{{\color{Orchid} y} = {\color{SkyBlue} x} + n} $$
- Let us assume we have access to examples of $ {\color{SkyBlue} x}$ without noise.
- We learn the distribution of noiseless data $\log p_\theta(x)$ from samples using a deep generative model.
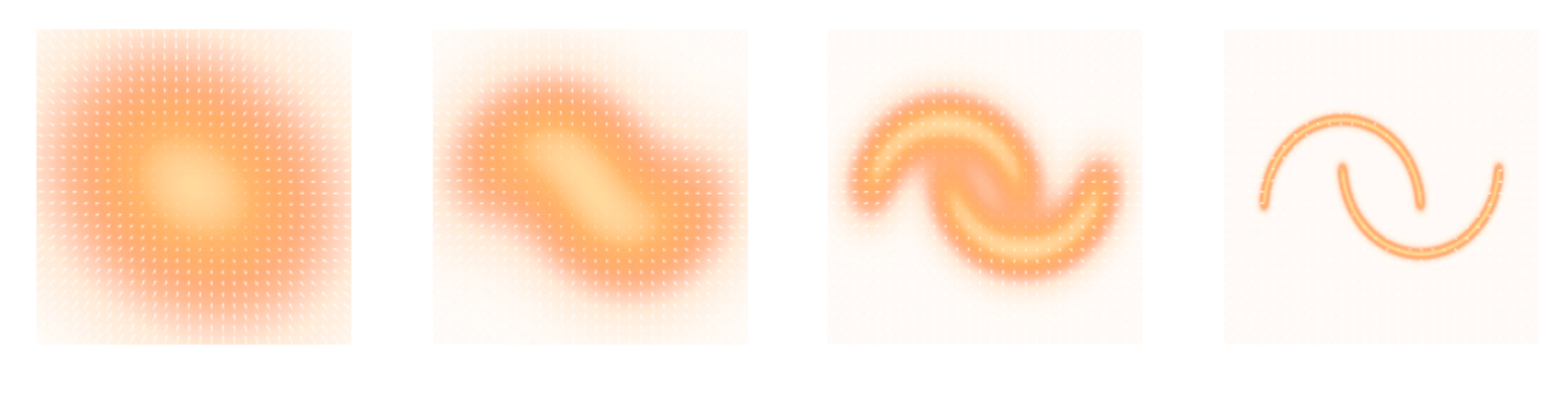
- The solution should lie on the realistic data manifold, symbolized by the two-moons distribution.
We want to solve for the Maximum A Posterior solution:
$$\arg \max - \frac{1}{2} \parallel {\color{Orchid} y} - {\color{SkyBlue} x} \parallel_2^2 + \log p_\theta({\color{SkyBlue} x})$$ This can be done by gradient descent as long as one has access to the score function $\frac{\color{orange} d \color{orange}\log \color{orange}p\color{orange}(\color{orange}x\color{orange})}{\color{orange} d \color{orange}x}$.
High-Dimensional Bayesian Inference for Inverse Problems With Neural Score Estimation



Work in collaboration with:
Benjamin Remy, Zaccharie Ramzi


$\Longrightarrow$ Learn complex priors by Neural Score Estimation and sample from posterior with gradient-based MCMC.

Let's set the stage: Gravitational lensing
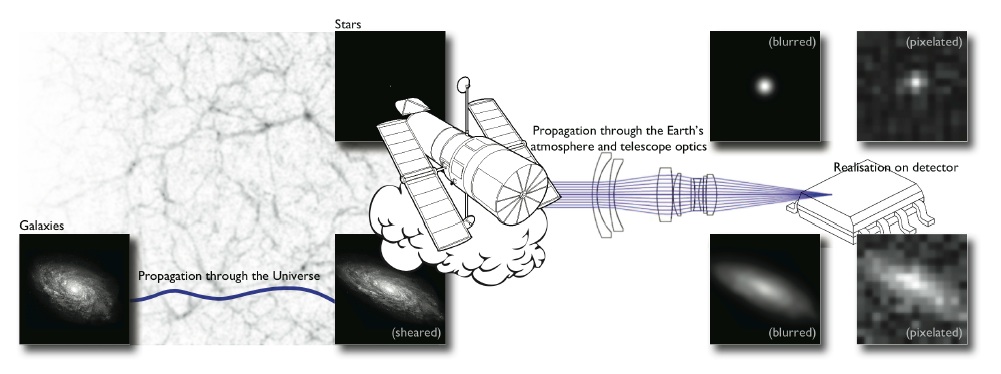
Galaxy shapes as estimators for gravitational shear
$$ e = \gamma + e_i \qquad \mbox{ with } \qquad e_i \sim \mathcal{N}(0, I)$$
- We are trying the measure the ellipticity $e$ of galaxies as an estimator for the gravitational shear $\gamma$
Gravitational Lensing as an Inverse Problem
Shear $\gamma$
![]()
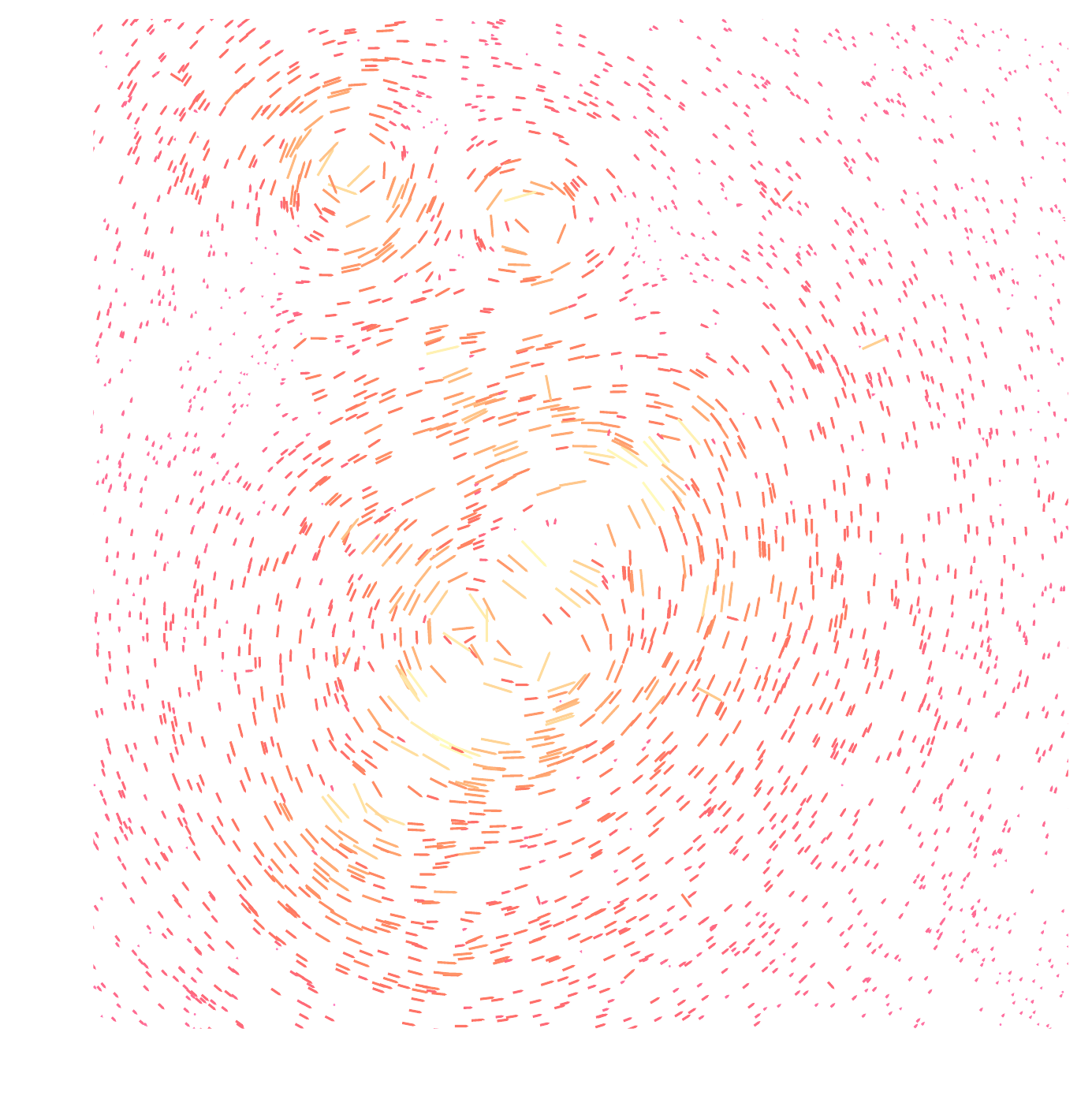
Convergence $\kappa$
![]()
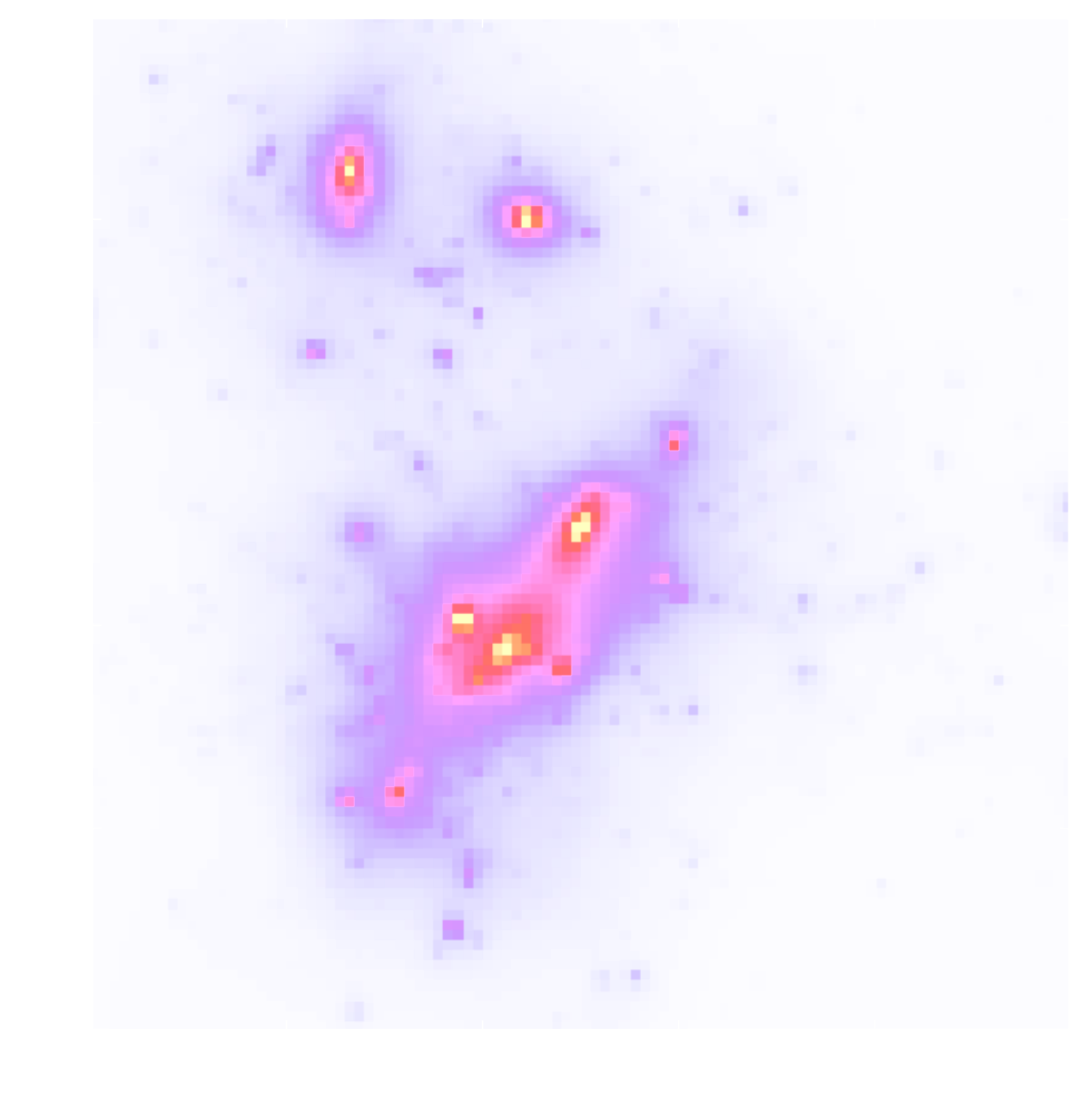
$$\gamma_1 = \frac{1}{2} (\partial_1^2 - \partial_2^2) \ \Psi \quad;\quad \gamma_2 = \partial_1 \partial_2 \ \Psi \quad;\quad \kappa = \frac{1}{2} (\partial_1^2 + \partial_2^2) \ \Psi$$
$$\boxed{\gamma = \mathbf{P} \kappa}$$
Illustration on the Dark Energy Survey (DES) Y3
Jeffrey, et al. (2021)
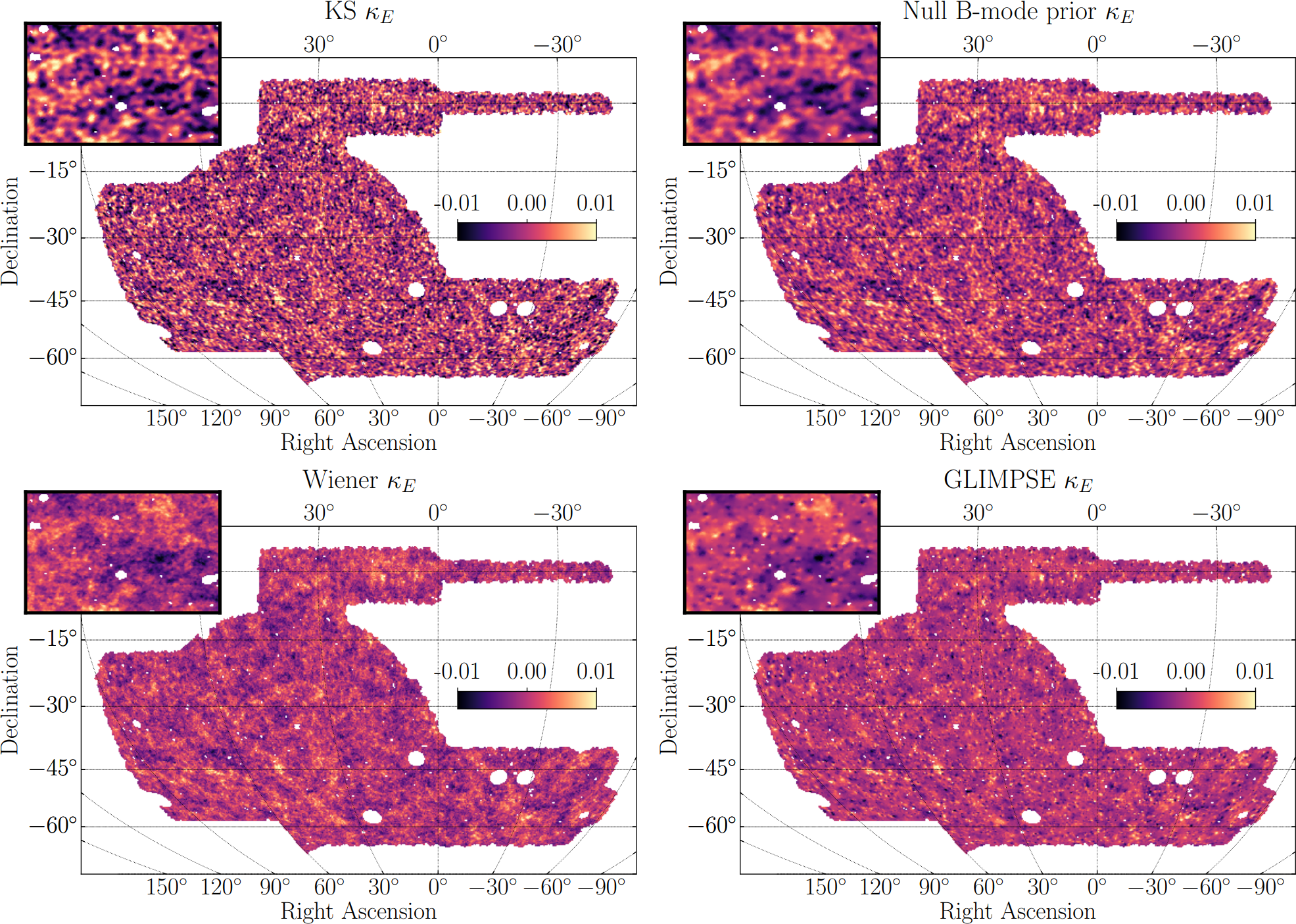
Writing down the convergence map log posterior
$$ \log p( \kappa | e) = \underbrace{\log p(e | \kappa)}_{\simeq -\frac{1}{2} \parallel e - P \kappa \parallel_\Sigma^2} + \log p(\kappa) +cst $$- The likelihood term is known analytically, given to us by the physics of gravitational lensing.
- There is no close form expression for the prior on dark matter maps $\kappa$.
However:- We do have access to samples of full implicit prior through simulations: $X = \{x_0, x_1, \ldots, x_n \}$ with $x_i \sim \mathbb{P}$
![]()
- We do have access to samples of full implicit prior through simulations: $X = \{x_0, x_1, \ldots, x_n \}$ with $x_i \sim \mathbb{P}$
$\Longrightarrow$ Our strategy: Learn the prior from simulation,
and then sample the full posterior.
How do you do this in practice in very high dimensional problems?
First realization: The score is all you need!
- Whether you are looking for the MAP or sampling with HMC or MALA, you
only need access to the score of the posterior:
$$\frac{\color{orange} d \color{orange}\log \color{orange}p\color{orange}(\color{orange}x \color{orange}|\color{orange} y\color{orange})}{\color{orange}
d
\color{orange}x}$$
- Gradient descent: $x_{t+1} = x_t + \tau \nabla_x \log p(x_t | y) $
- Langevin algorithm: $x_{t+1} = x_t + \tau \nabla_x \log p(x_t | y) + \sqrt{2\tau} n_t$

- The score of the full posterior is simply: $$\nabla_x \log p(x |y) = \underbrace{\nabla_x \log p(y |x)}_{\mbox{known explicitly}} \quad + \quad \underbrace{\nabla_x \log p(x)}_{\mbox{known implicitly}}$$ $\Longrightarrow$ "all" we have to do is model/learn the score of the prior.
Neural Score Estimation by Denoising Score Matching (Vincent 2011)
- Denoising Score Matching: An optimal Gaussian denoiser learns the score of a given distribution.
- If $x \sim \mathbb{P}$ is corrupted by additional Gaussian noise $u \in \mathcal{N}(0, \sigma^2)$ to yield $$x^\prime = x + u$$
- Let's consider a denoiser $r_\theta$ trained under an $\ell_2$ loss: $$\mathcal{L}=\parallel x - r_\theta(x^\prime, \sigma) \parallel_2^2$$
- The optimal denoiser $r_{\theta^\star}$ verifies: $$\boxed{\boldsymbol{r}_{\theta^\star}(\boldsymbol{x}', \sigma) = \boldsymbol{x}' + \sigma^2 \nabla_{\boldsymbol{x}} \log p_{\sigma^2}(\boldsymbol{x}')}$$
$\boldsymbol{x}'$
$\boldsymbol{x}$
$\boldsymbol{x}'- \boldsymbol{r}^\star(\boldsymbol{x}', \sigma)$
$\boldsymbol{r}^\star(\boldsymbol{x}', \sigma)$

Second Realization: Annealing is everything!
- Even with knowledge of the score, sampling in high number of dimensions is difficult!
- Convolving a target distribution $p$ with a noise kernel, makes $p_\sigma(x) = \int \mathcal{N}(x; x^\prime, \sigma^2) (x^\prime) d x^{\prime}$ it much better behaved
$$\sigma_1 > \sigma_2 > \sigma_3 > \sigma_4 $$
![]()
- Hints to running many MCMC chains in parallel, progressively annealing the $\sigma$ to 0, keep last point in the chain as independent sample.
Score-Based Generative Modeling Song et al. (2021)
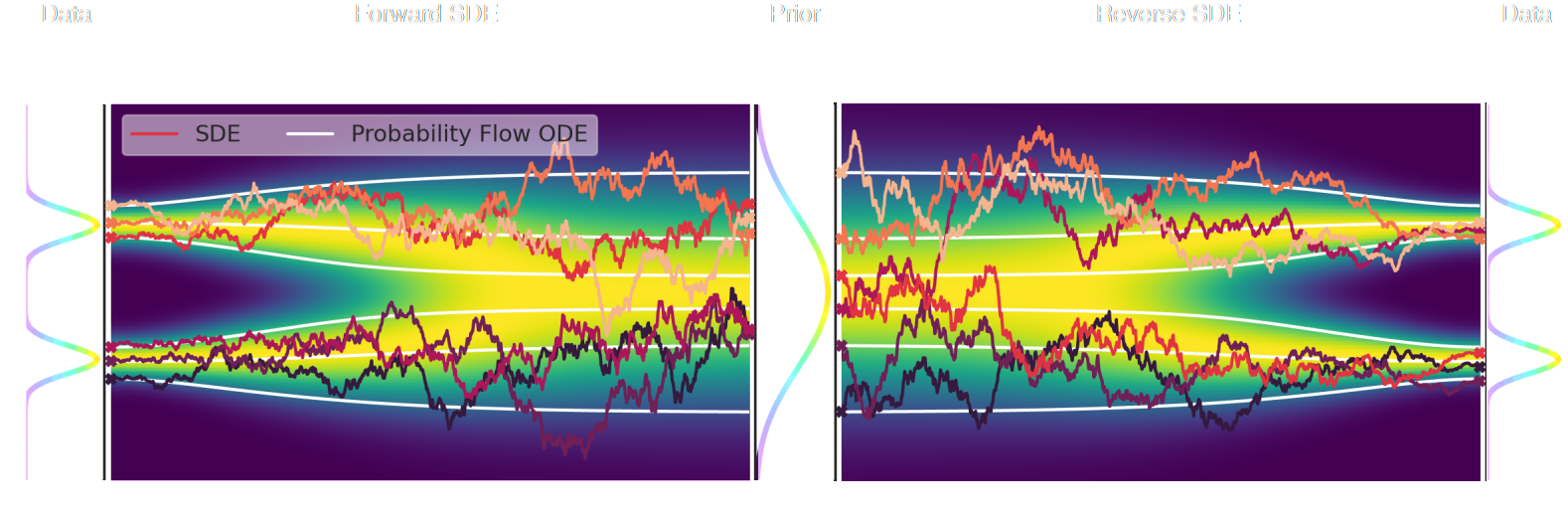
- The SDE defines a marginal distribution $p_t(x)$ as the convolution of the target distribution $p(x)$ with a noise kernel $p_{t|s}(\cdot | x_s)$: $$p_t(x) = \int p(x_s) p_{t|s}(x | x_s) d x_s$$
- For a given forward SDE that evolves $p(x)$ to $p_T(x)$, there exists a reverse SDE that evolves $p_T(x)$ back into $p(x)$. It involves having access to the marginal score $\nabla_x \log_t p(x)$.
Third realization: We don't actually know the marginal posterior score!
- We know the following quantities:
- Annealed likelihood (analytically): $p_\sigma(y | x) = \mathcal{N}(y; \mathbf{A} x, \mathbf{\Sigma} + \sigma^2 \mathbf{I})$
- Annealed prior score (by score matching): $\nabla_x \log p_\sigma(x)$
- But, unfortunately: $\boxed{p_\sigma(x|y) \neq p_\sigma(y|x) \ p_\sigma(x)}$ $\Longrightarrow$ We don't know the marginal posterior score!
- We cannot use the reverse SDE/ODE of diffusion models to sample from the posterior. $$\mathrm{d} x = [f(x, t) - g^2(t) \underbrace{\nabla_x \log p_t(x|y)}_{\mbox{unknown}} ] \mathrm{d}t + g(t) \mathrm{d} w$$
Proposed sampling strategy
- Even if not equivalent to the marginal posterior score, $\nabla_x \log p_{\sigma^2}(y | x) + \nabla_x \log p_{\sigma^2}(x)$ still
has good properties:
- Tends to an isotropic Gaussian distribution for large $\sigma$
- Corresponds to the target posterior for $\sigma=0$
- If we simulate this SDE sufficiently slowly (i.e. timescale of change of $\sigma$ is much larger than the timescale of the SDE) we can expect to sample from the target posterior.
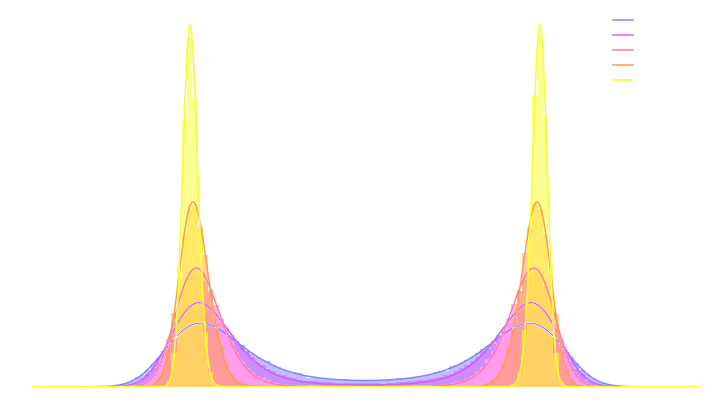
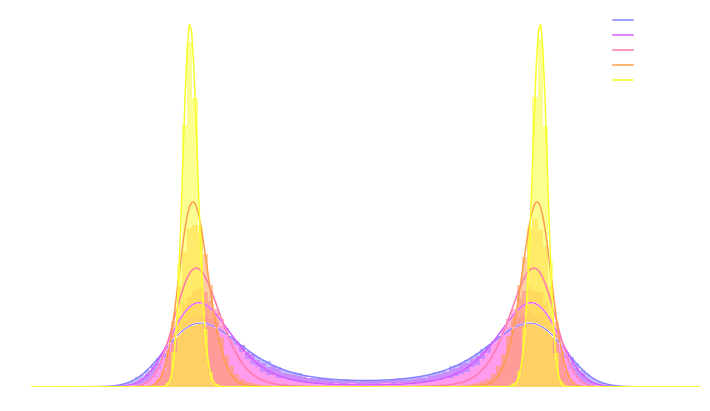
$\Longrightarrow$ In practice, we sample the annealed distribution using an Hamiltonian Monte-Carlo,
with discrete annealing steps.
Example of one chain during annealing
Validating Posterior Sampling under a Gaussian prior
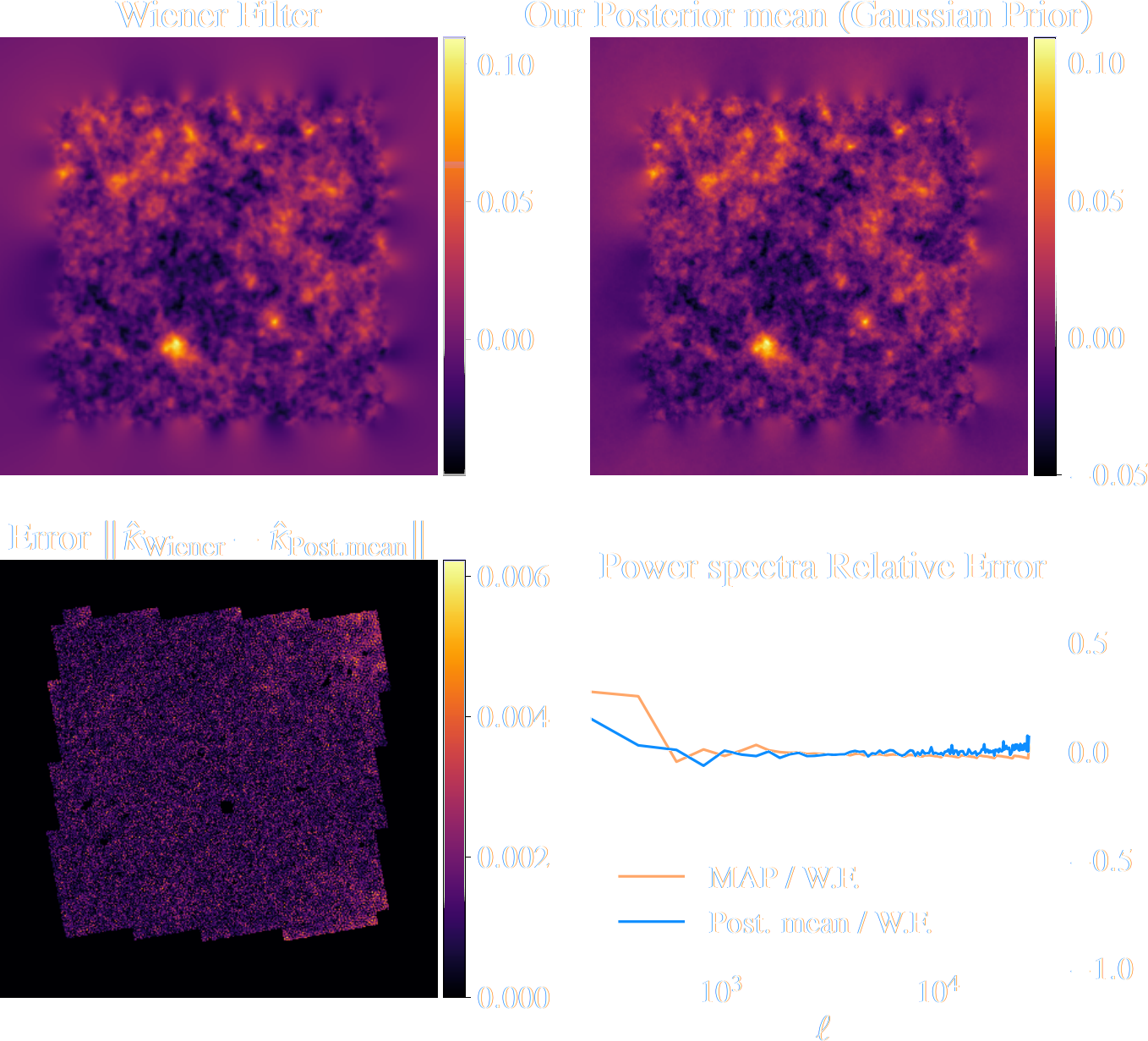
Illustration on $\kappa$-TNG simulations

True convergence map

Traditional Kaiser-Squires
Wiener Filter
Posterior Mean (ours)

Posterior samples
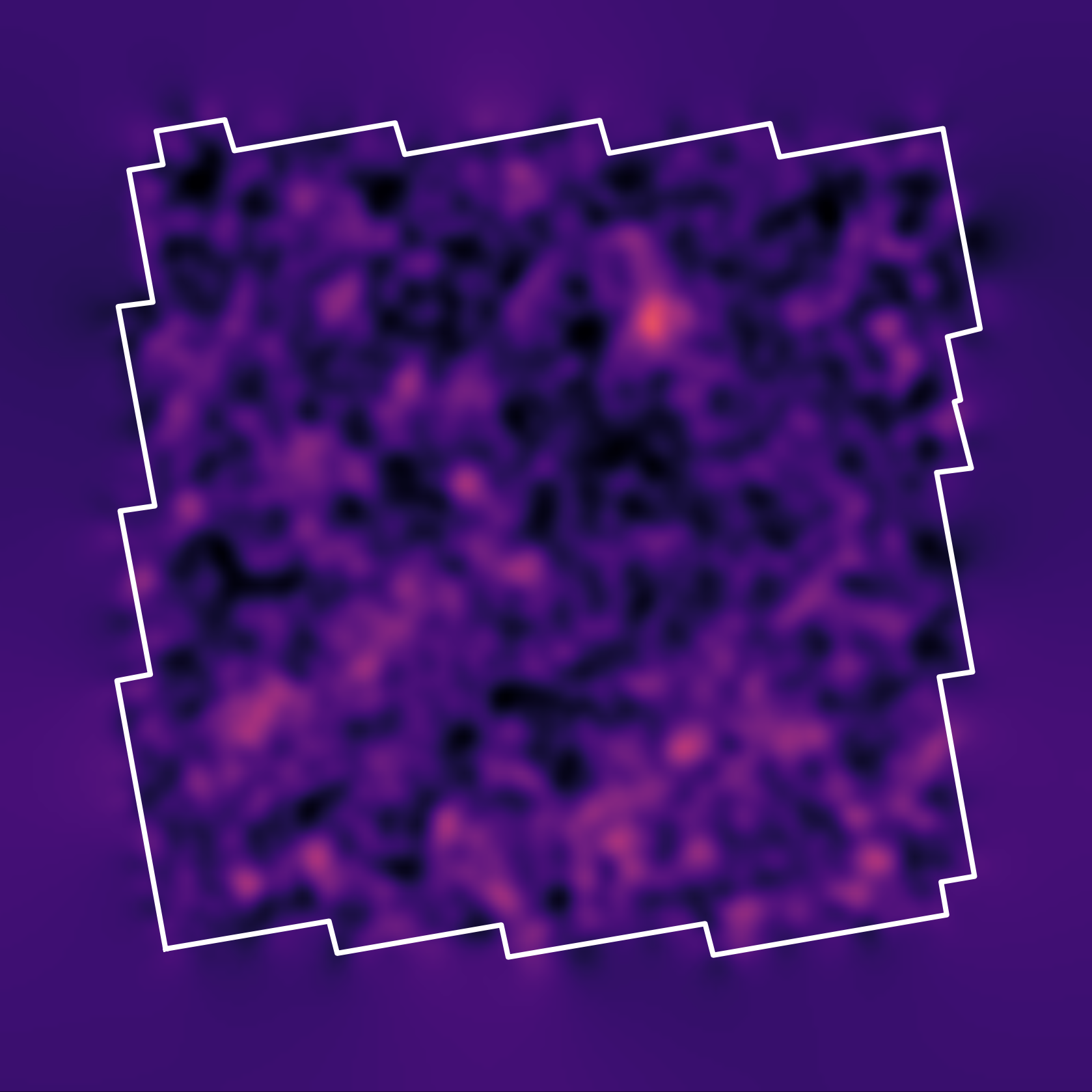
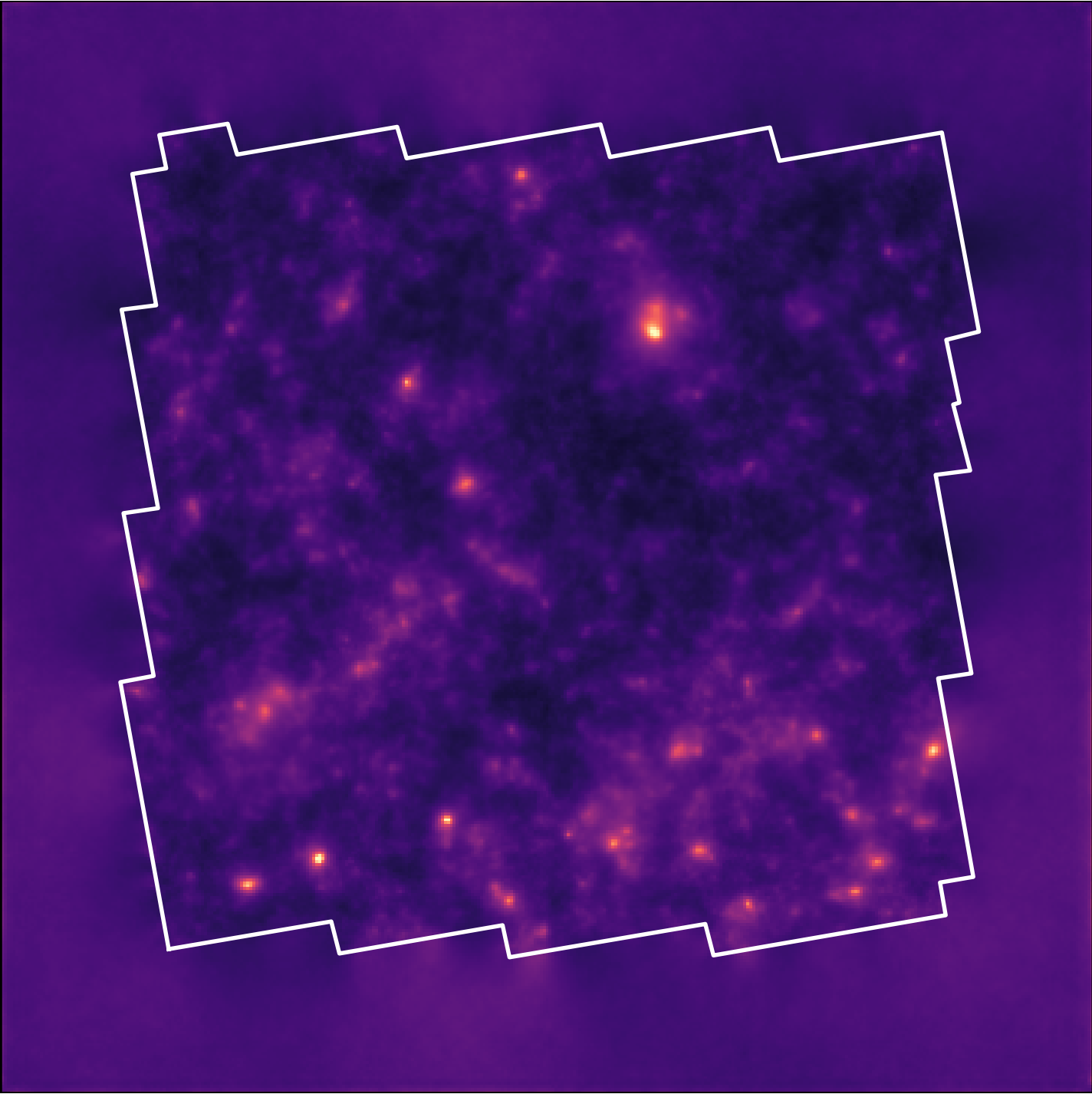
Reconstruction of the HST/ACS COSMOS field
- COSMOS shear data from Schrabback et al. 2010
- Prior learned from $\kappa$-TNG simulation from Osato et al. 2021.
Massey et al. (2007)
![]()
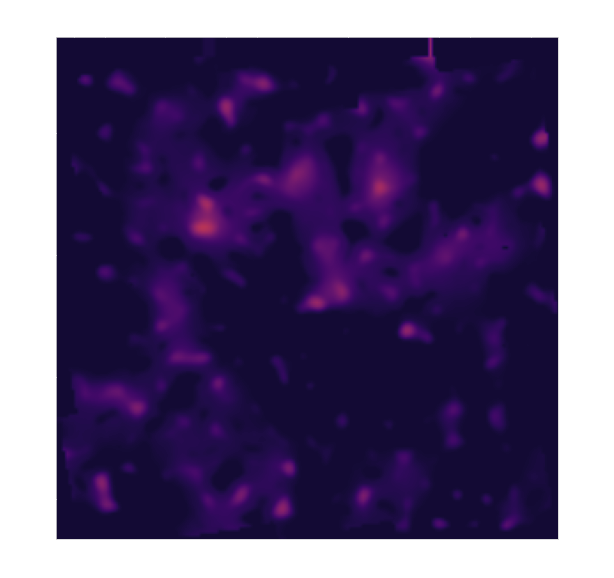
Remy et al. (2022) Posterior mean
![]()
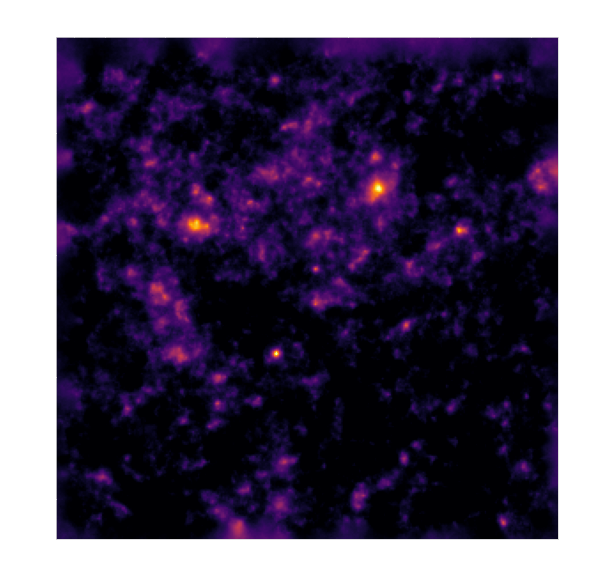
Remy et al. (2022) Posterior samples
![]()
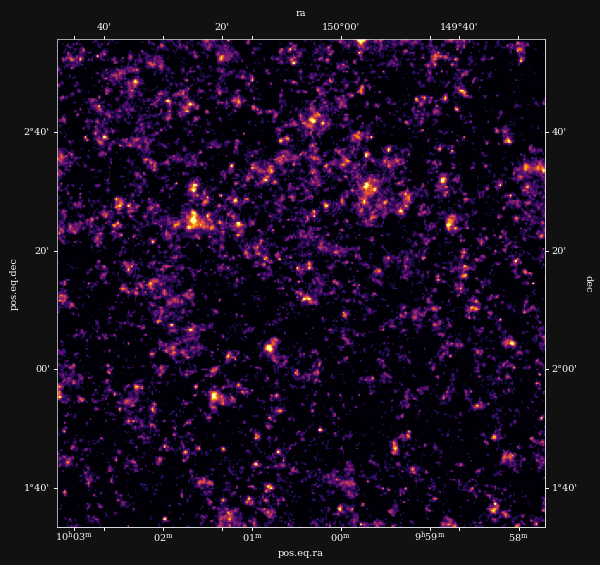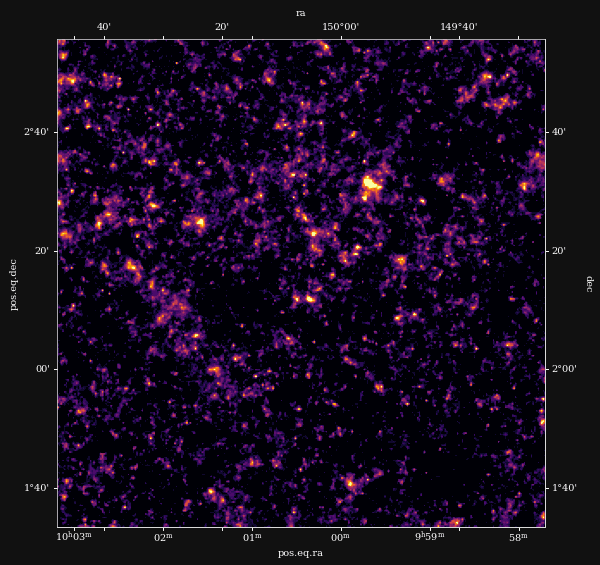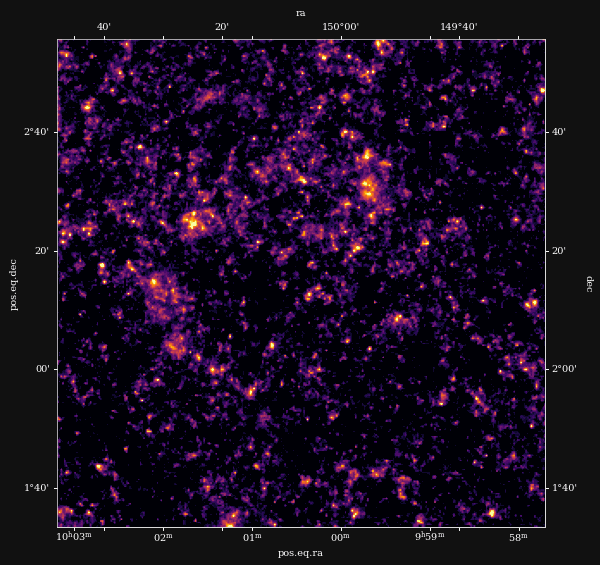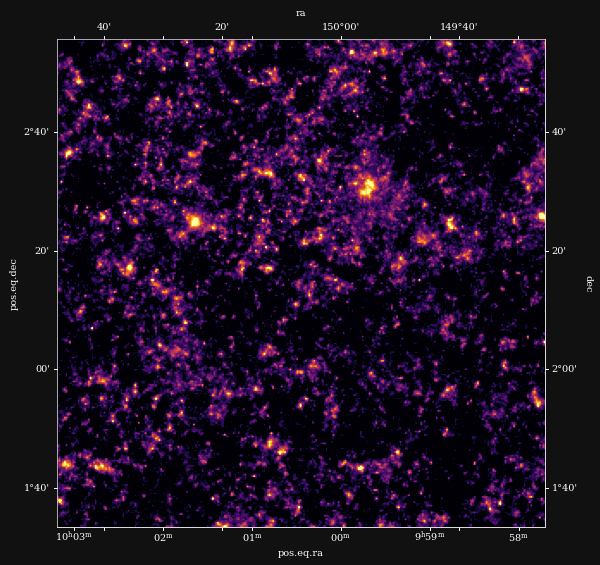
Other examples of Deep Priors
Variational Inference over Hybrid Hierarchical Bayesian Models


Work led by Benjamin Remy

$\Longrightarrow$ Eliminate model bias in shear inference by using data-driven morphology priors.

Impact of galaxy morphology on shape measurement


Mandelbaum, et al. (2013), Mandelbaum, et al. (2014)
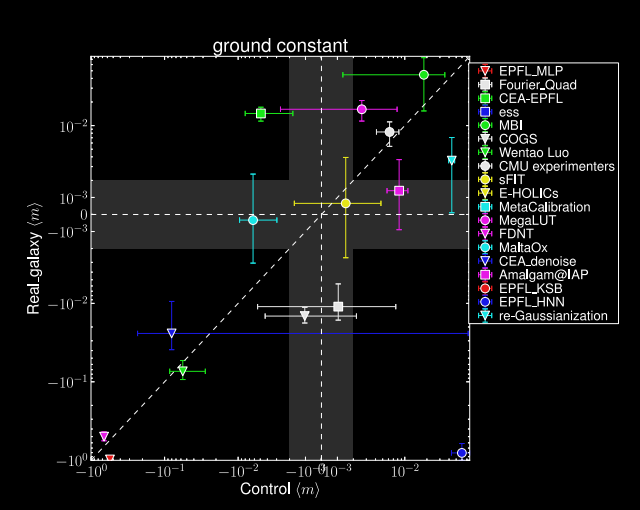
$\Longrightarrow$ Let's learn a prior from this implicit distribution!
Complications specific to astronomical images: spot the differences!

CelebA

HSC PDR-2 wide
- There is noise
- We have a Point Spread Function (instrumental response)
A Physicist's approach: let's build a model





$\longrightarrow$
$g_\theta$
$g_\theta$
$\longrightarrow$
PSF
PSF
$\longrightarrow$
Pixelation
Pixelation
$\longrightarrow$
Noise
Noise

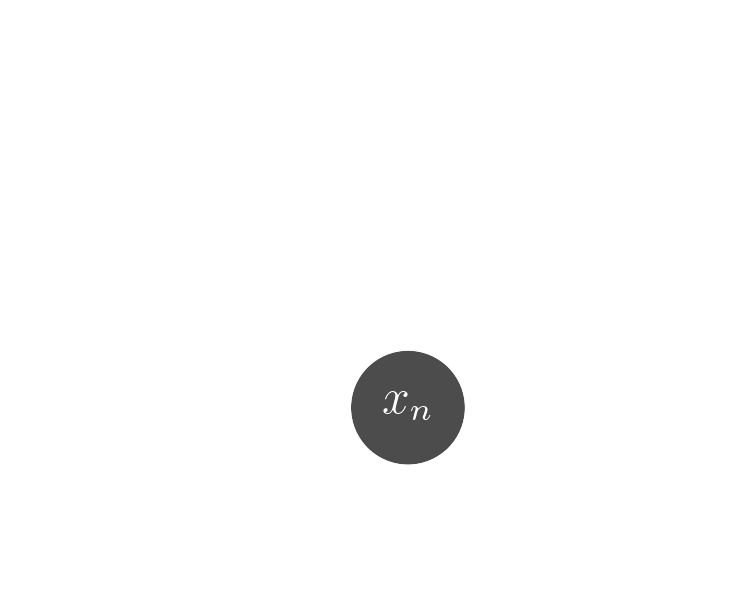

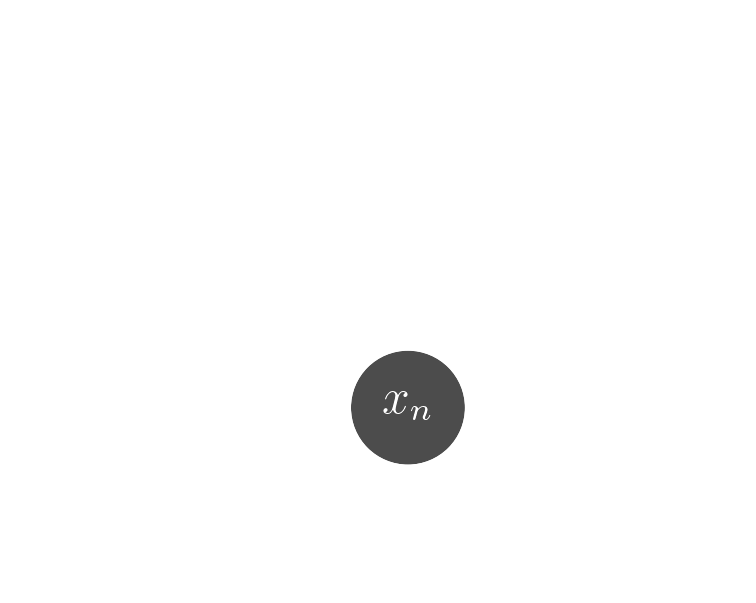
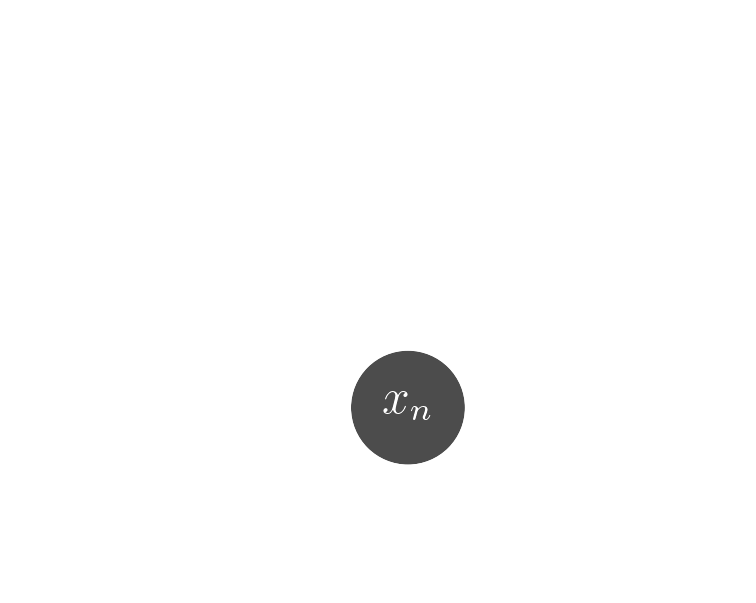
Probabilistic model
$$ x \sim ? $$
$$ x \sim \mathcal{N}(z, \Sigma) \quad z \sim ? $$
latent $z$ is a denoised galaxy image
latent $z$ is a denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} z, \Sigma) \quad z \sim ?$$
latent $z$ is a super-resolved and denoised galaxy image
latent $z$ is a super-resolved and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast z), \Sigma) \quad z \sim ? $$
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast g_\theta(z)), \Sigma) \quad z \sim \mathcal{N}(0, \mathbf{I}) $$
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
$\Longrightarrow$ Decouples the morphology model from the observing conditions.
How to train your dragon model
- Training the generative amounts to finding $\theta_\star$ that
maximizes the marginal likelihood of the model:
$$p_\theta(x | \Sigma, \Pi) = \int \mathcal{N}( \Pi \ast g_\theta(z), \Sigma) \ p(z) \ dz$$
$\Longrightarrow$ This is generally intractable
- Efficient training of parameter $\theta$ is made possible by Amortized Variational Inference.
Auto-Encoding Variational Bayes (Kingma & Welling, 2014)
- We introduce a parametric distribution $q_\phi(z | x, \Pi, \Sigma)$ which aims to model the posterior $p_{\theta}(z | x, \Pi, \Sigma)$.
- Working out the KL divergence between these two distributions leads to: $$\log p_\theta(x | \Sigma, \Pi) \quad \geq \quad - \mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]$$ $\Longrightarrow$ This is the Evidence Lower-Bound, which is differentiable with respect to $\theta$ and $\phi$.
The famous Variational Auto-Encoder
$$\log p_\theta(x| \Sigma, \Pi ) \geq - \underbrace{\mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right)}_{\mbox{code regularization}} + \underbrace{\mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]}_{\mbox{reconstruction error}} $$
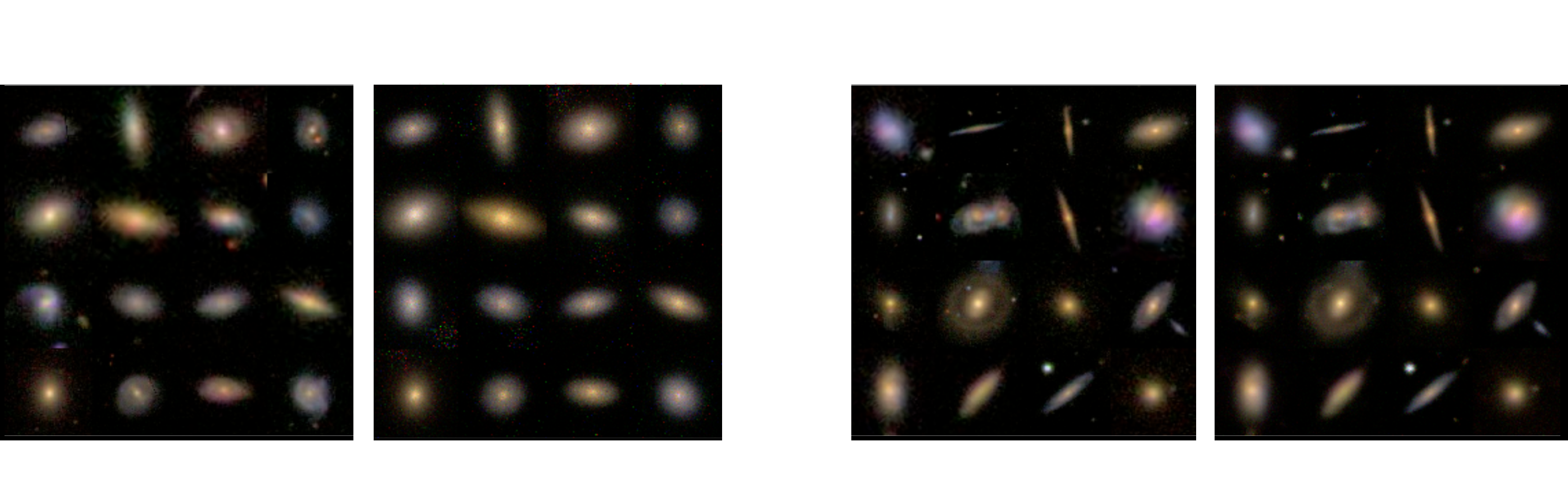
Sampling from the model
 Woups... what's going on?
Woups... what's going on?
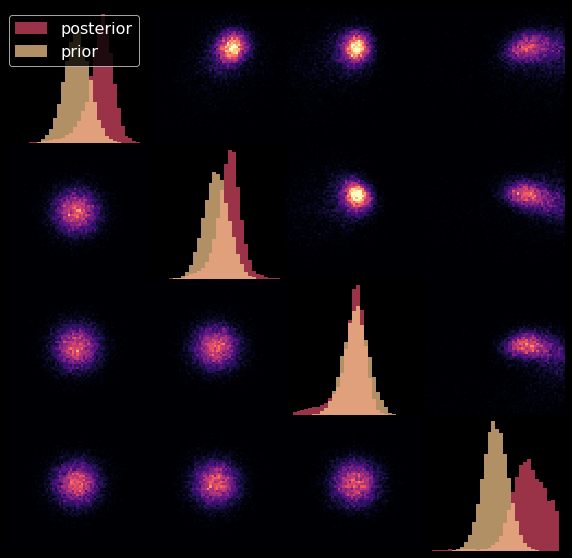
Tradeoff between code regularization and image quality
$$\log p_\theta(x| \Sigma, \Pi ) \geq - \underbrace{\mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right)}_{\mbox{code regularization}} + \underbrace{\mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]}_{\mbox{reconstruction error}} $$
Latent space modeling with Normalizing Flows
$\Longrightarrow$ All we need to do is sample from the aggregate posterior of the data instead of sampling from the prior.
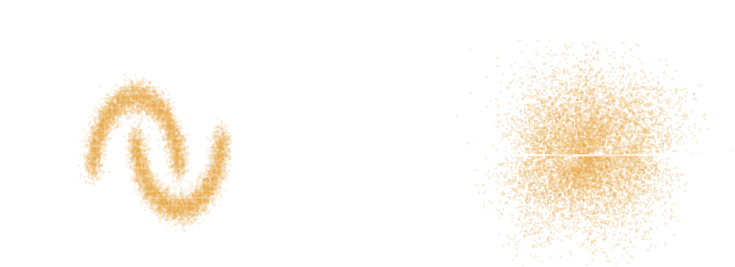
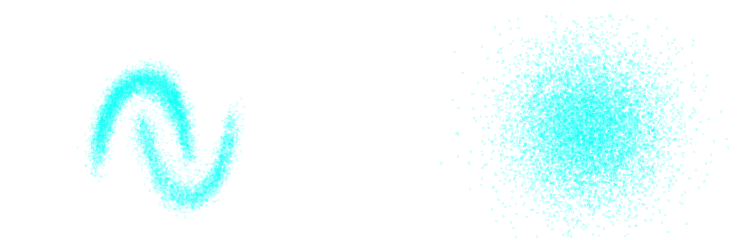
Dinh et al. 2016
Normalizing Flows
- Assumes a bijective mapping between data space $x$ and latent space $z$ with prior $p(z)$: $$ z = f_{\theta} ( x ) \qquad \mbox{and} \qquad x = f^{-1}_{\theta}(z)$$
- Admits an explicit marginal likelihood: $$ \log p_\theta(x) = \log p(z) + \log \left| \frac{\partial f_\theta}{\partial x} \right|(x) $$
Flow-VAE samples

How do I use my generative model to infer gravitational lensing?
Let's again think as physicists





$\longrightarrow$
$g_\theta$
$g_\theta$
$\longrightarrow$
shear $\gamma$
shear $\gamma$
$\longrightarrow$
PSF
PSF
$\longrightarrow$
Noise
Noise
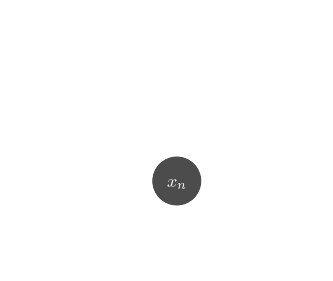
Probabilistic model
$$ x \sim \mathcal{N}(\Pi \ast
(g_\theta(z) \otimes \gamma), \Sigma) \quad z \sim \mathcal{N}(0,
\mathbf{I}) $$
latent $z$ are morphological parameters
$\theta$ are global parameters of the model
$\gamma$ are shear parameters
latent $z$ are morphological parameters
$\theta$ are global parameters of the model
$\gamma$ are shear parameters
$\Longrightarrow$ We have a hybrid probabilistic model, with the known physics of lensing and of the instrument, and
learned morphology model.
Joint inference using a parametric model for the morphology
Let's assume that $g(z)$ is a sersic model, i.e. $z = \{n, r_\text{hlr}, F, e_1, e_2, s_x, s_y\}$ and
$$g(z) = F \times I_0 \exp \left( -b_n \left[\left( \frac{r}{r_\text{hlr}}\right)^{\frac{1}{n}} -1\right] \right)$$
We need a more realistic model of galaxy morphology
The joint inference of $p(z, \gamma | \mathcal{D})$ leads to a biased posterior...
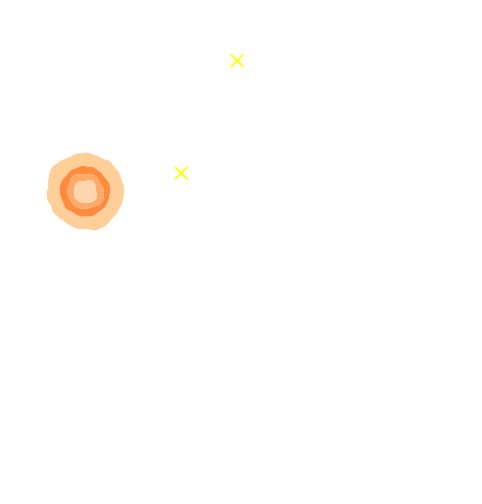
Marginal shear posterior $p(\gamma|\mathcal{D})$
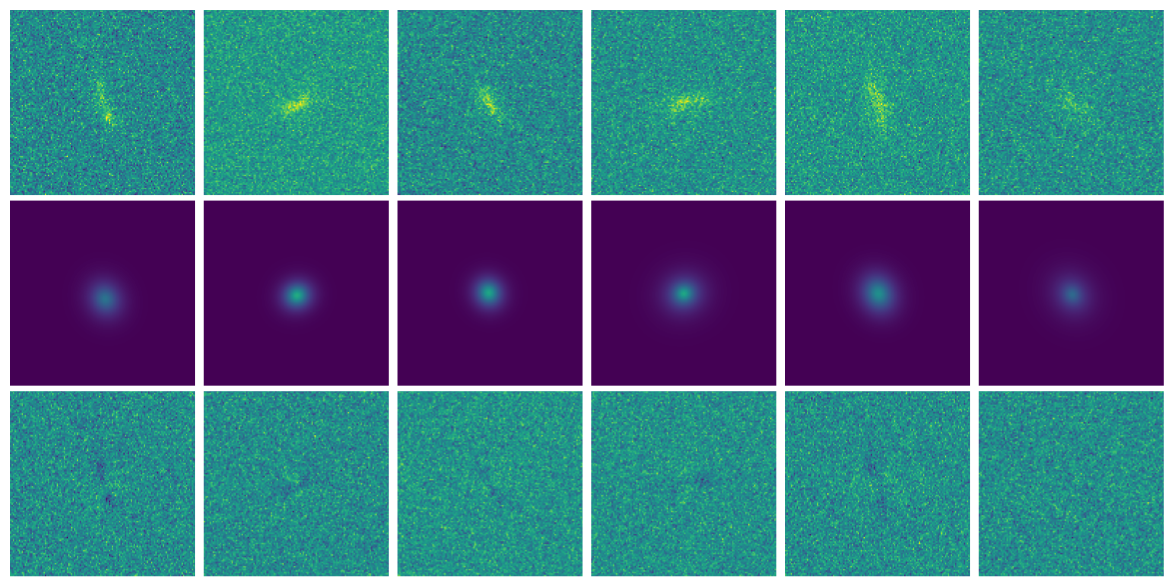
Maximum a posteriori fit and residuals

Marginal shear posterior $p(\gamma|\mathcal{D})$

Maximum a posteriori fit and residuals
We need a more realistic model of galaxy morphology
Joint inference using a generative model for the morpholgy
Let's use a learned $g_\theta(z)$
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suite of N-body + raytracing simulations: $\mathcal{D}$
![]()
![]()
Towards Optimal Full-Field Implicit Inference


![]()
![]()
![]()
![]()
DifferentiableUniverseInitiative/sbi_lens
JAX-based log-normal lensing simulation package![]()
![]()
![]()
![]()
![]()
simulated observed data
posterior samples $\kappa = f(z,\theta)$ with $z \sim p(z, \theta | x)$
![]()
![]()
![]()
![]()
$$F = - \mathbb{E}_{p(x | \theta)}[ H_\theta(\log p(x| \theta)) ] $$

![]()
![]()
DES Y1 posterior, jax-cosmo HMC vs Cobaya MH
(credit: Joe Zuntz)
![]() Linear Field
Linear Field
![]() Final Dark Matter
Final Dark Matter
![]() Dark Matter Halos
Dark Matter Halos
![]() Galaxies
Galaxies
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


Work in collaboration with:
![]()
$\Longrightarrow$ Learn residuals to known physical equations to improve accuracy of fast PM simulations.
![]()
![]()
![]()
![]()
Neural network trained using single CAMELS simulation of $25^3$ ($h^{-1}$ Mpc)$^3$ volume and $64^3$ dark matter particles at the fiducial cosmology of $\Omega_m = 0.3$
![]()
![]()
![]() Linear Field
Linear Field
![]() Final Dark Matter
Final Dark Matter
![]() Dark Matter Halos
Dark Matter Halos
![]() Galaxies
Galaxies
![]()
https://github.com/DifferentiableUniverseInitiative/DHOD
![]()
The joint inference of $p(z, \gamma | \mathcal{D})$ leads to an unbiased posterior!
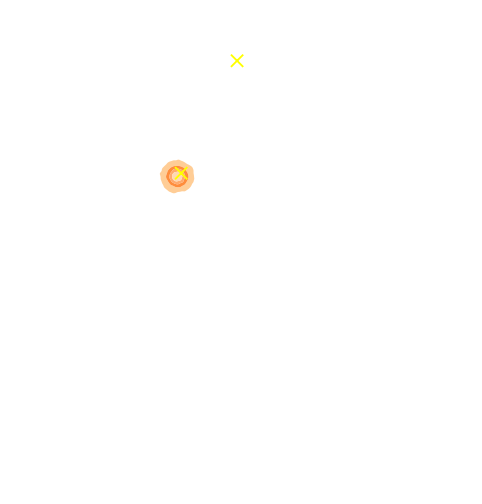
Marginal shear posterior $p(\gamma|\mathcal{D})$

Maximum a posteriori fit and residuals

Marginal shear posterior $p(\gamma|\mathcal{D})$

Maximum a posteriori fit and residuals
takeaways
Benefits of Bayesian forward modeling for inverse problems
Using a Bayesian approach has great advantages: model-based physical interpretation & uncertainty quantification.
- Explicit likelihood, uses of all of our physical knowledge.
$\Longrightarrow$ The method can be applied for varying noise, observing conditions, or different instruments - Deep generative models can be used to provide simulation or data driven priors.
$\Longrightarrow$ Embed prior only accessible from samples (e.g. numerical simulations or data). - For the first time, we have the tools to sample complex high-dimensional posteriors!
Simulation-Based Inference
Leveraging Physical Simulators for Inference
The limits of traditional cosmological inference
HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
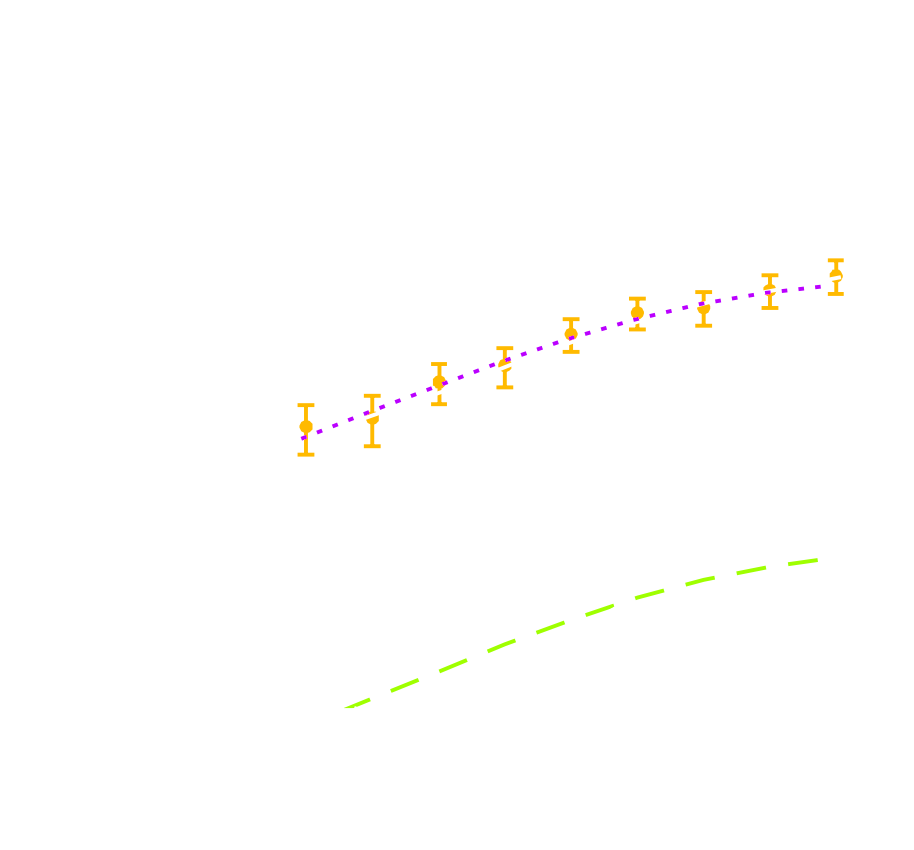
(Hikage et al. 2018)
- Measure the ellipticity $\epsilon = \epsilon_i + \gamma$ of all galaxies
$\Longrightarrow$ Noisy tracer of the weak lensing shear $\gamma$ - Compute summary statistics based on 2pt functions,
e.g. the power spectrum - Run an MCMC to recover a posterior on model parameters, using an analytic likelihood $$ p(\theta | x ) \propto \underbrace{p(x | \theta)}_{\mathrm{likelihood}} \ \underbrace{p(\theta)}_{\mathrm{prior}}$$
Main limitation: the need for an explicit likelihood
We can only compute from theory the likelihood for simple summary statistics and on large scales
$\Longrightarrow$ We are dismissing a significant fraction of the information!
Full-Field Simulation-Based Inference
- Instead of trying to analytically evaluate the likelihood of
sub-optimal summary statistics, let us build a forward model of the full observables.
$\Longrightarrow$ The simulator becomes the physical model. - Each component of the model is now tractable, but at the cost of a large number of latent variables.
Benefits of a forward modeling approach
- Fully exploits the information content of the data (aka "full field inference").
- Easy to incorporate systematic effects.
- Easy to combine multiple cosmological probes by joint simulations.
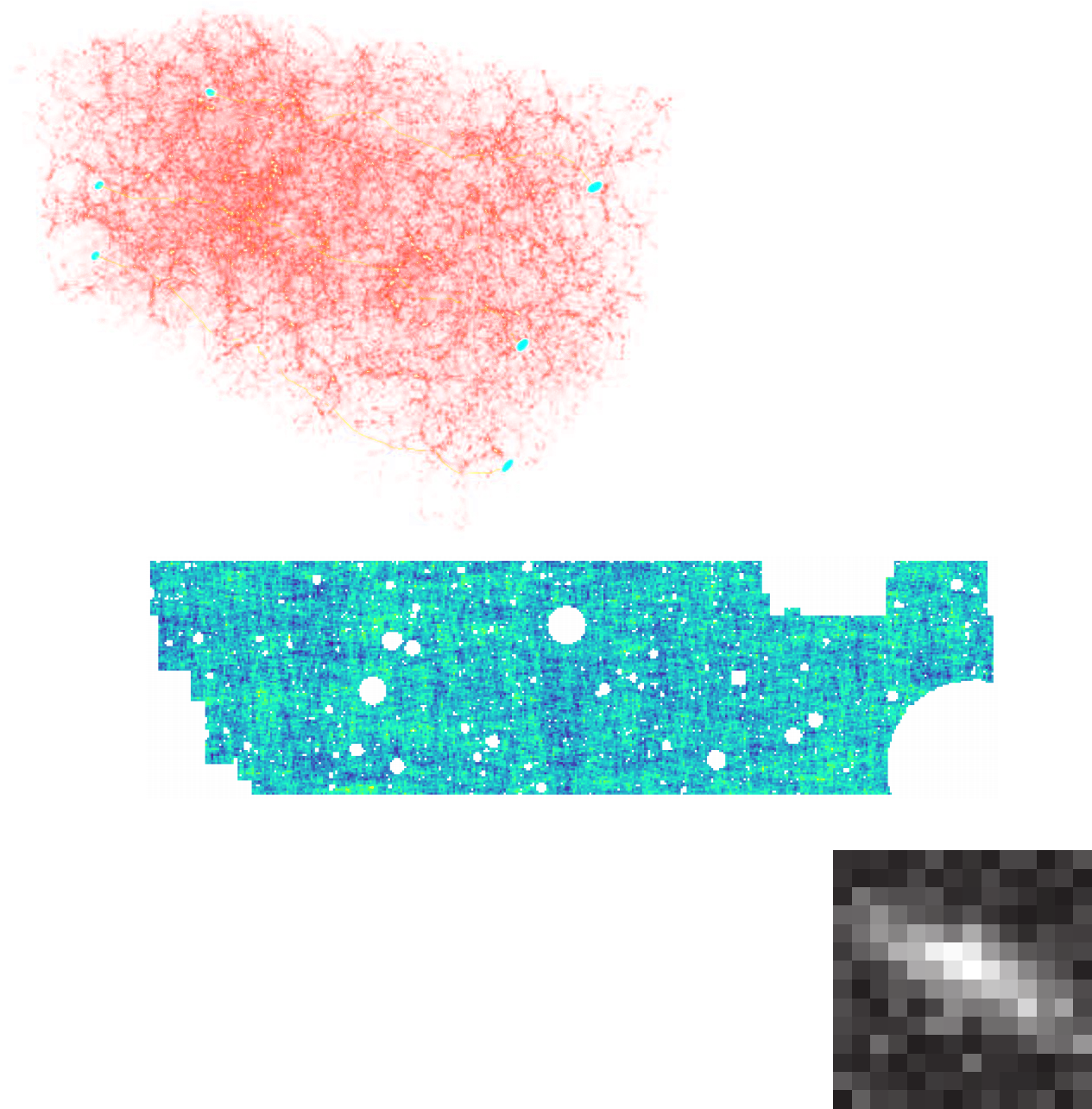
(Porqueres et al. 2021)
For this talk, let's ignore the elephant in the room:
Do we have reliable enough models for the full complexity of the data?
Do we have reliable enough models for the full complexity of the data?
...so why is this not mainstream?
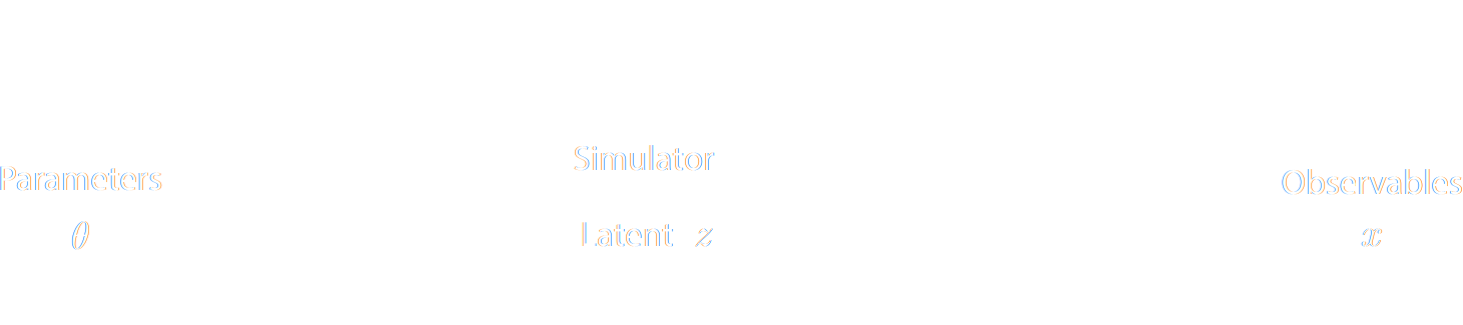

The Challenge of Simulation-Based Inference
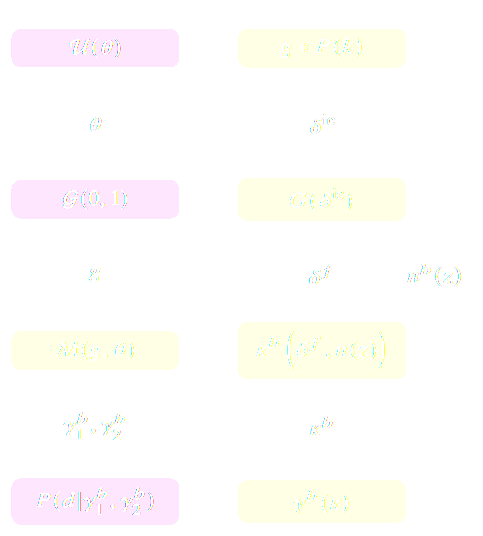
$$ p(x|\theta) = \int p(x, z | \theta) dz = \int p(x | z, \theta) p(z | \theta) dz $$
Where $z$ are stochastic latent variables of the simulator.
$\Longrightarrow$ This marginal likelihood is intractable!
$\Longrightarrow$ This marginal likelihood is intractable!
How to perform inference over forward simulation models?
- Implicit Inference: Treat the simulator as a black-box with only the ability to sample from the joint distribution
$$(x, \theta) \sim p(x, \theta)$$
a.k.a.
- Simulation-Based Inference (SBI)
- Likelihood-free inference (LFI)
- Approximate Bayesian Computation (ABC)
- Explicit Inference: Treat the simulator as a probabilistic model and perform inference over the joint posterior
$$p(\theta, z | x) \propto p(x | z, \theta) p(z, \theta) p(\theta) $$
a.k.a.
- Bayesian Hierarchical Modeling (BHM)
$\Longrightarrow$ For a given simulation model, both methods should converge to the same posterior!
Implicit Inference
The land of Neural Density Estimation
Black-box Simulators Define Implicit Distributions

- A black-box simulator defines $p(x | \theta)$ as an implicit distribution, you can sample from it but you cannot evaluate it.
- Key Idea: Use a parametric distribution model $\mathbb{P}_\varphi$ to approximate the implicit distribution $\mathbb{P}$.
Conditional Density Estimation with Neural Networks
- I assume a forward model of the observations: \begin{equation} p( x ) = p(x | \theta) \ p(\theta) \nonumber \end{equation} All I ask is the ability to sample from the model, to obtain $\mathcal{D} = \{x_i, \theta_i \}_{i\in \mathbb{N}}$
- I am going to assume $q_\phi(\theta | x)$ a parametric conditional density
- Optimize the parameters $\phi$ of $q_{\phi}$ according to \begin{equation} \min\limits_{\phi} \sum\limits_{i} - \log q_{\phi}(\theta_i | x_i) \nonumber \end{equation} In the limit of large number of samples and sufficient flexibility \begin{equation} \boxed{q_{\phi^\ast}(\theta | x) \approx p(\theta | x)} \nonumber \end{equation}
$\Longrightarrow$ One can asymptotically recover the posterior by
optimizing a parametric estimator over
the Bayesian joint distribution
the Bayesian joint distribution
$\Longrightarrow$ One can asymptotically recover the posterior by
optimizing a Deep Neural Network over
a simulated training set.
a simulated training set.
My Practical Recipe to Apply Neural Density Estimation
A two-steps approach to Likelihood-Free Inference
- Step I Automatically learn a optimal low-dimensional summary statistic $$y = f_\varphi(x) $$ typically $y$ will have the same dimensionality as $\theta$.
- Step II: Use Neural Density Estimation in low dimension to either:
- build an estimate $p_\phi$ of the likelihood function $p(y \ | \ \theta)$ (Neural Likelihood Estimation)
- build an estimate $p_\phi$ of the posterior distribution $p(\theta \ | \ y)$ (Neural Posterior Estimation)
Automated Summary Statistics Extraction

- Introduce a parametric function $f_\varphi$ to reduce the dimensionality of the data while preserving information.
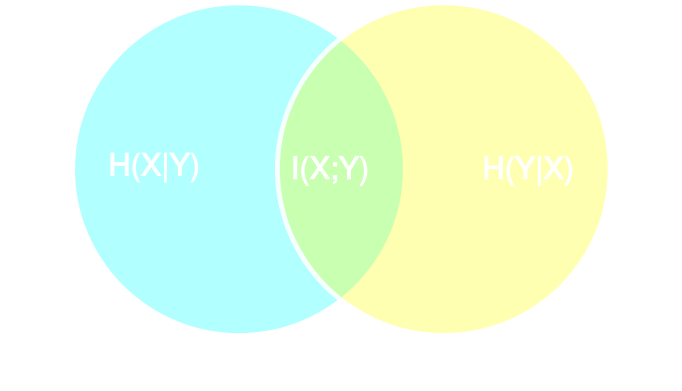
Information-based loss functions
- Summary statistics $y$ is sufficient for $\theta$ if, and only if, $$ I(Y; \Theta) = I(X; \Theta) \Leftrightarrow p(\theta | x ) = p(\theta | y) $$
- Variational Mutual Information Maximization $$ \mathcal{L} \ = \ \mathbb{E}_{x, \theta} [ \log q_\phi(\theta | f_\varphi(x)) ] \leq I(Y; \Theta) $$
Example of application: Infering Microlensing Event Parameters
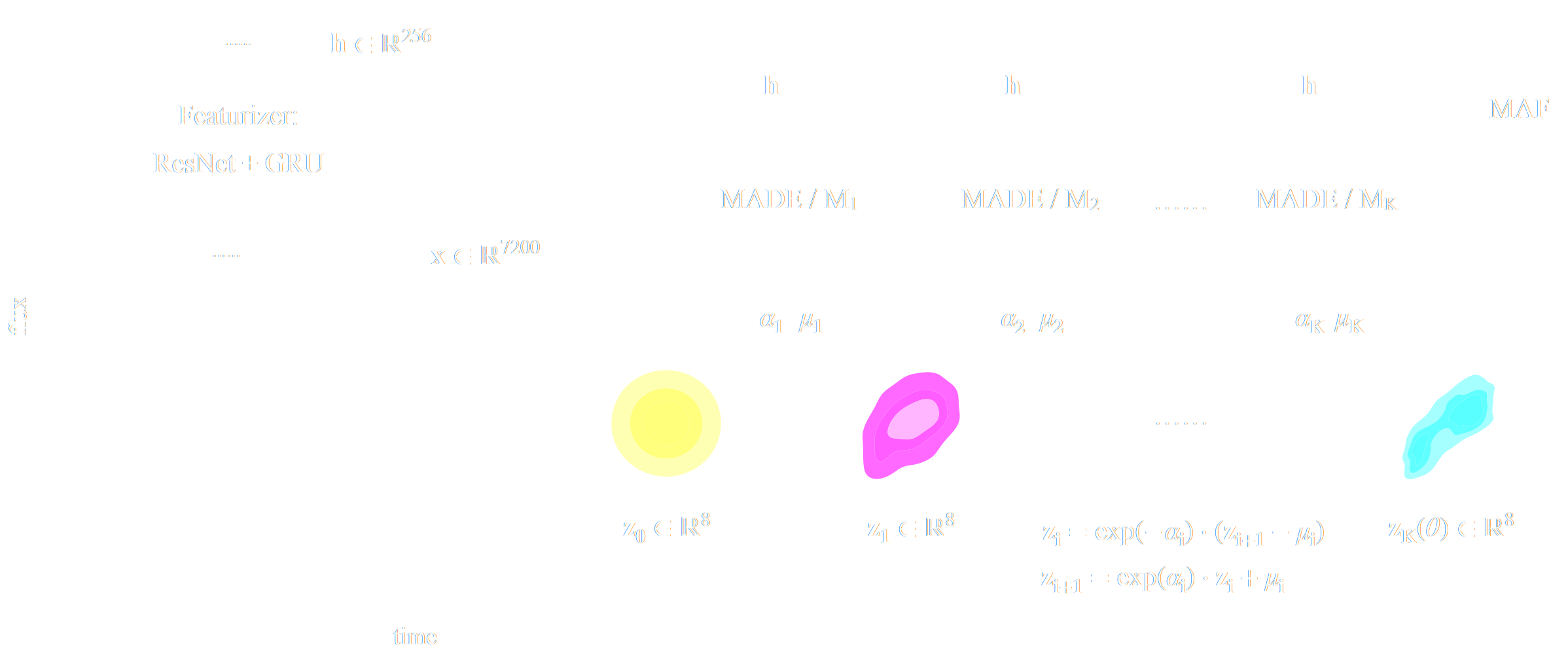
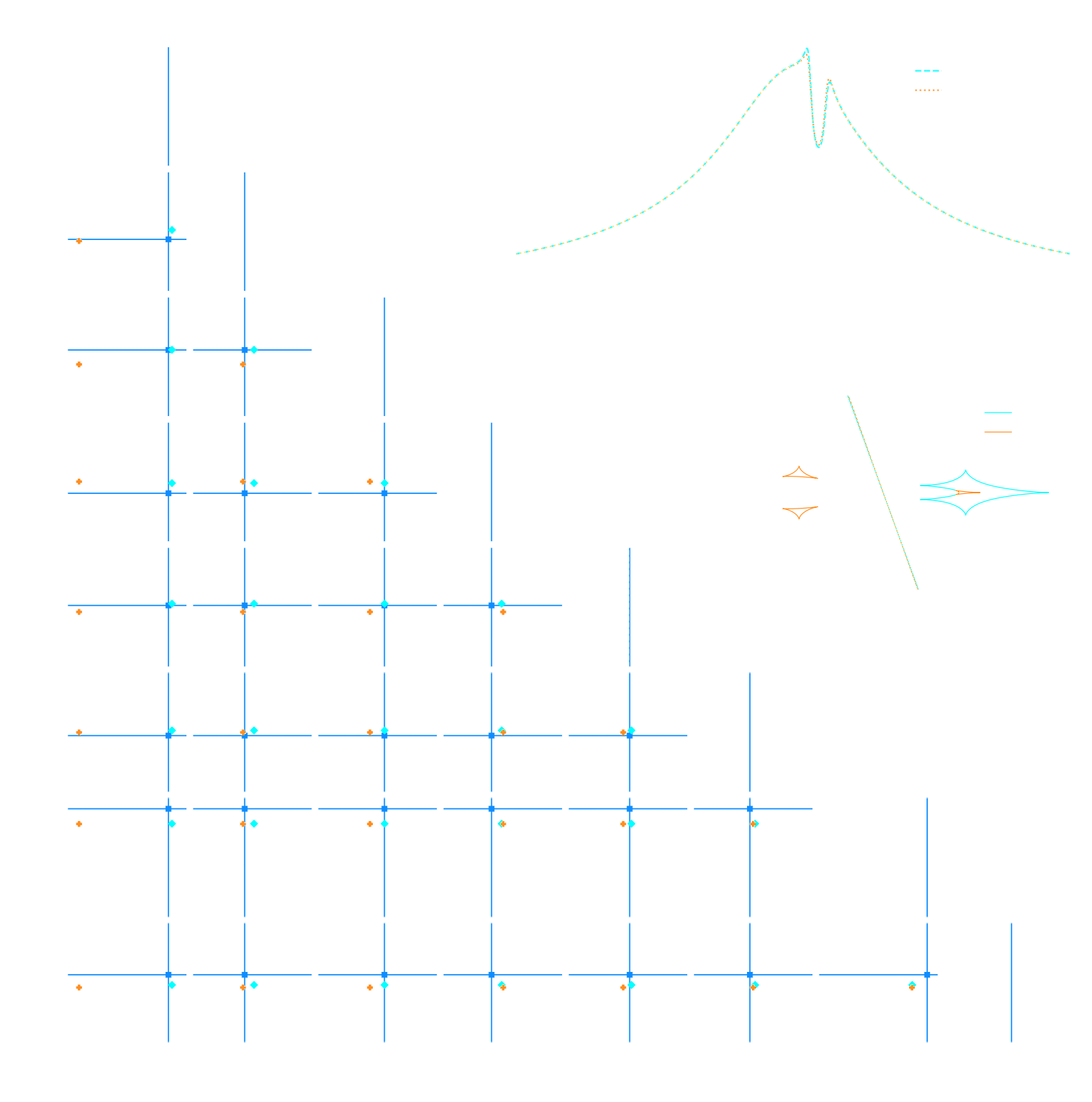
Example of application: Likelihood-Free parameter inference with DES SV
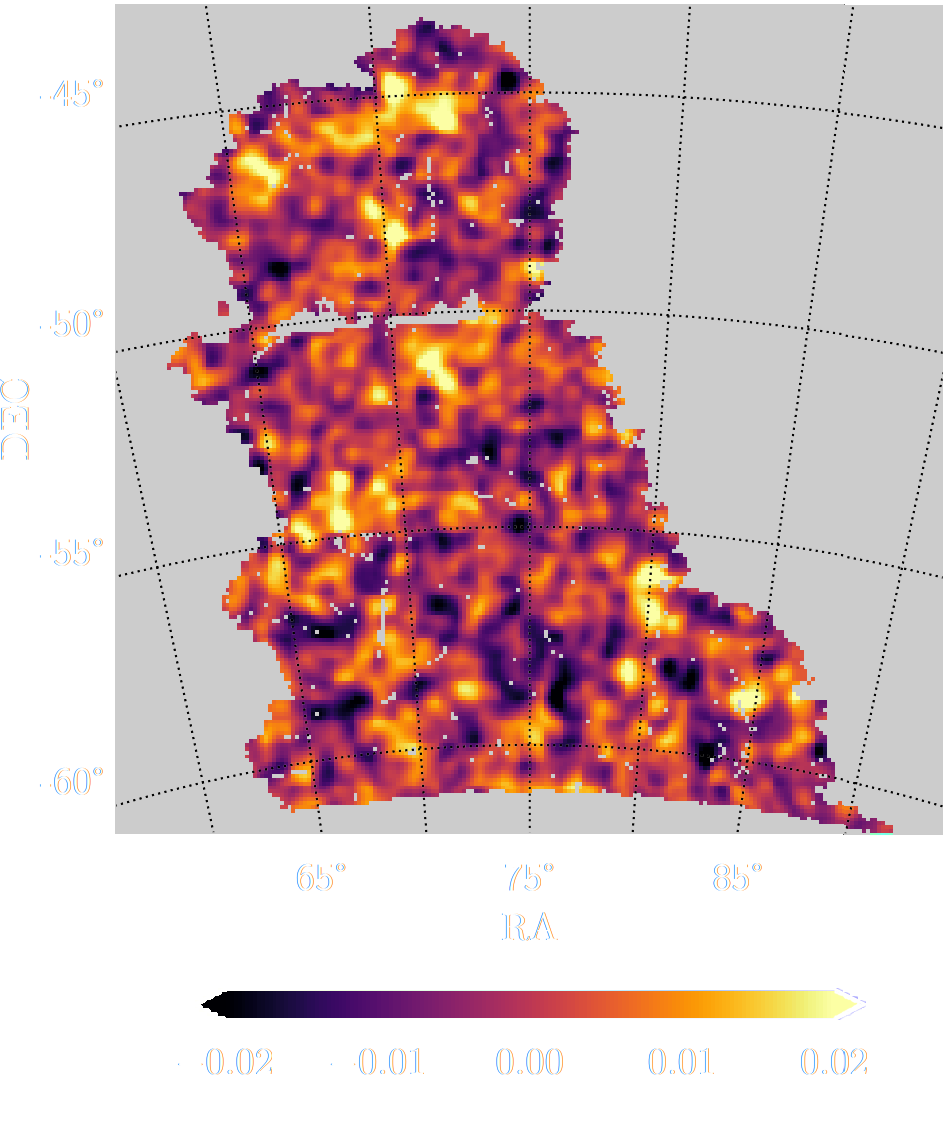
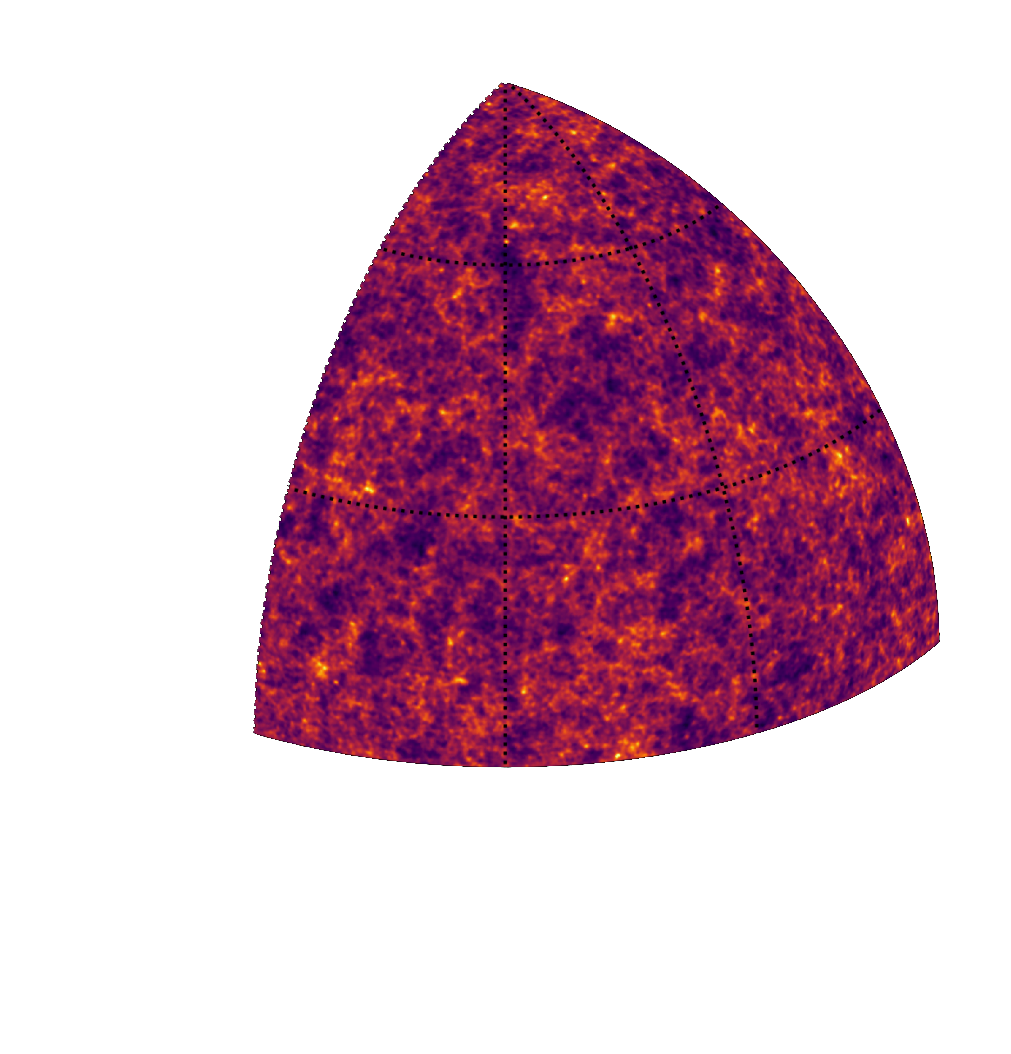
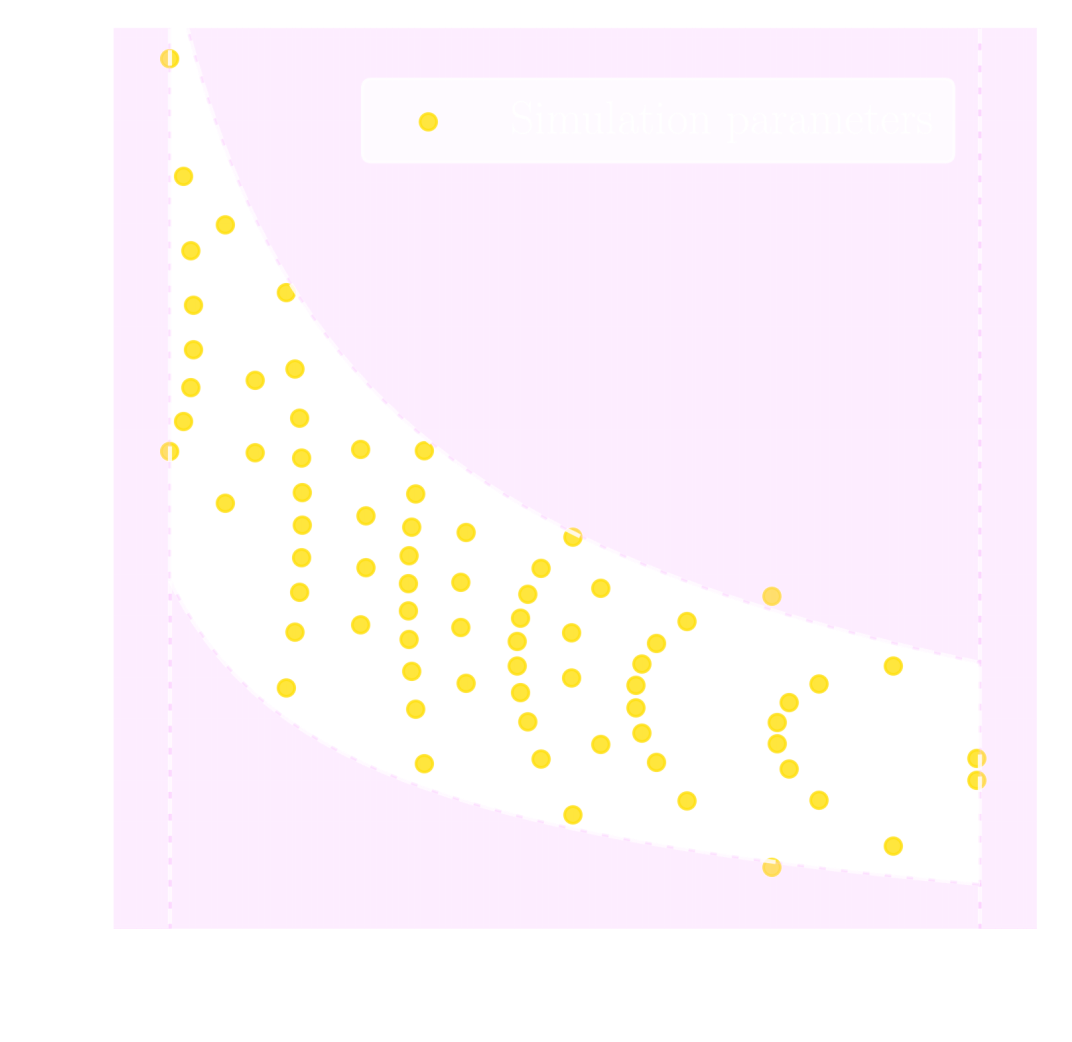
Suite of N-body + raytracing simulations: $\mathcal{D}$
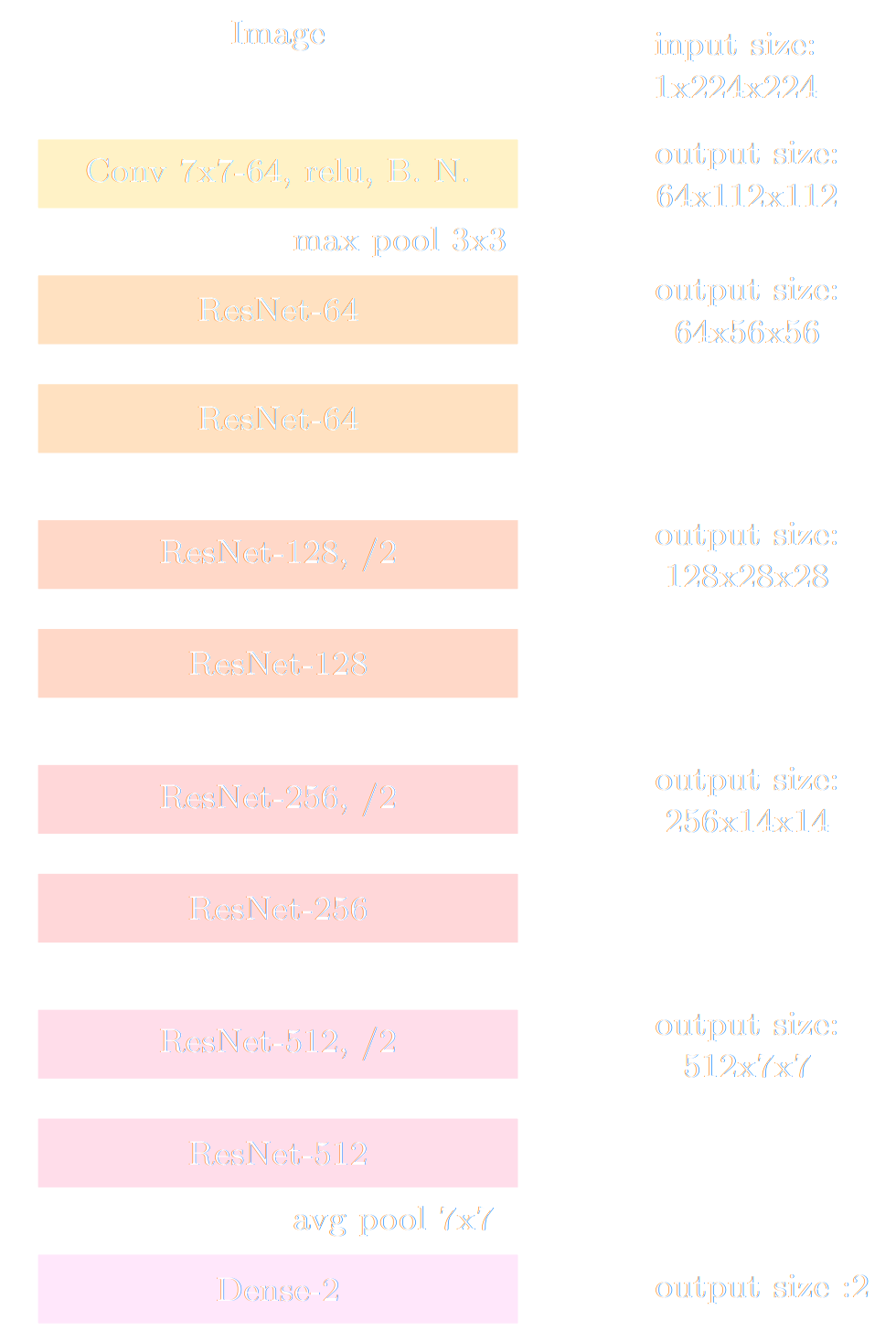
Towards Optimal Full-Field Implicit Inference
by Neural Summarisation and Density Estimation
Work led by Denise Lanzieri and Justine Zeghal

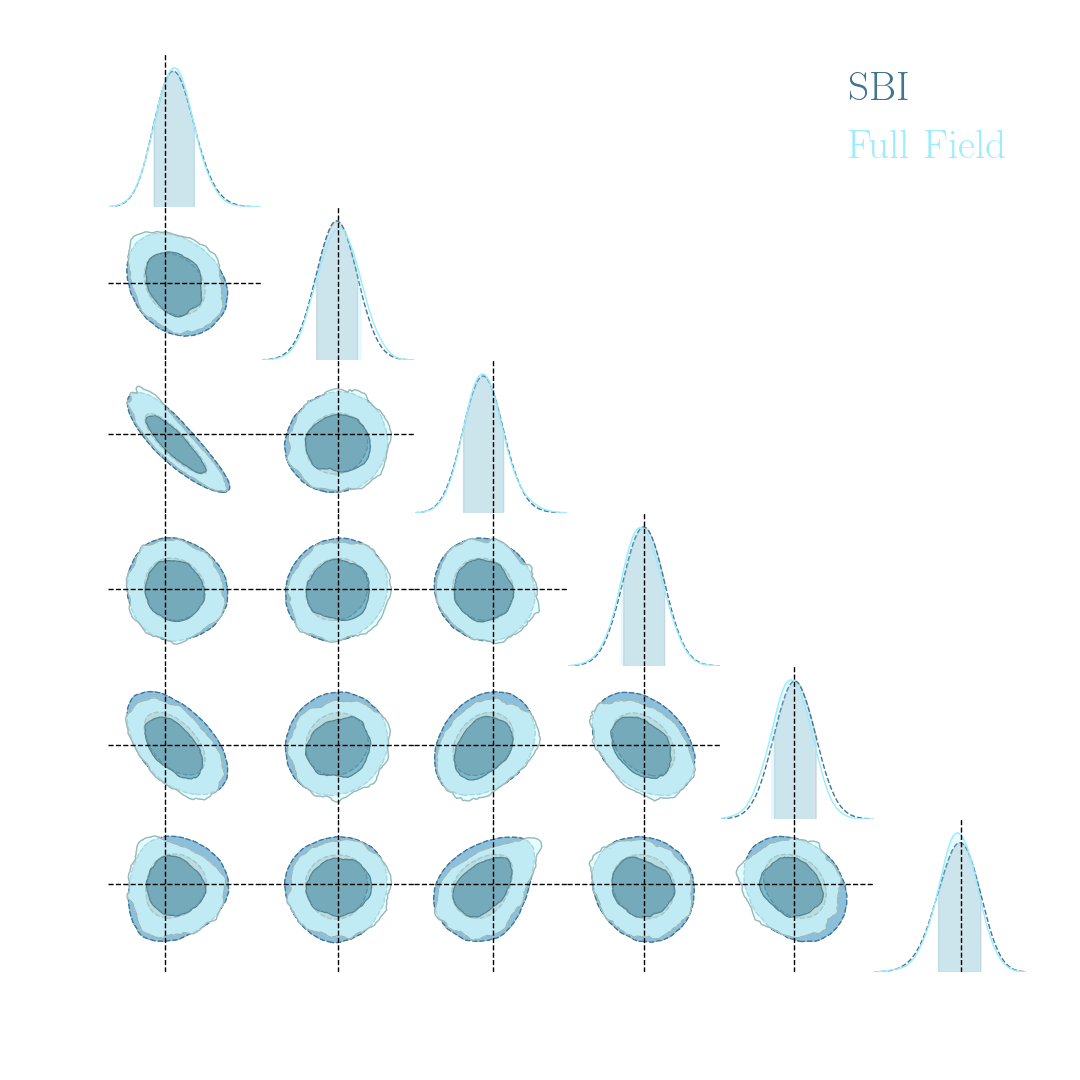
An easy-to-use validation testbed: log-normal lensing simulations

DifferentiableUniverseInitiative/sbi_lens
JAX-based log-normal lensing simulation package

- 10x10 deg$^2$ maps at LSST Y10 quality, conditioning the log-normal shift parameter on $(\Omega_m, \sigma_8, w_0)$
- Infer full-field posterior on cosmology:
- explicitly using an Hamiltonian-Monte Carlo (NUTS) sampler
- implicitly using a learned summary statistics and conditional density estimation.
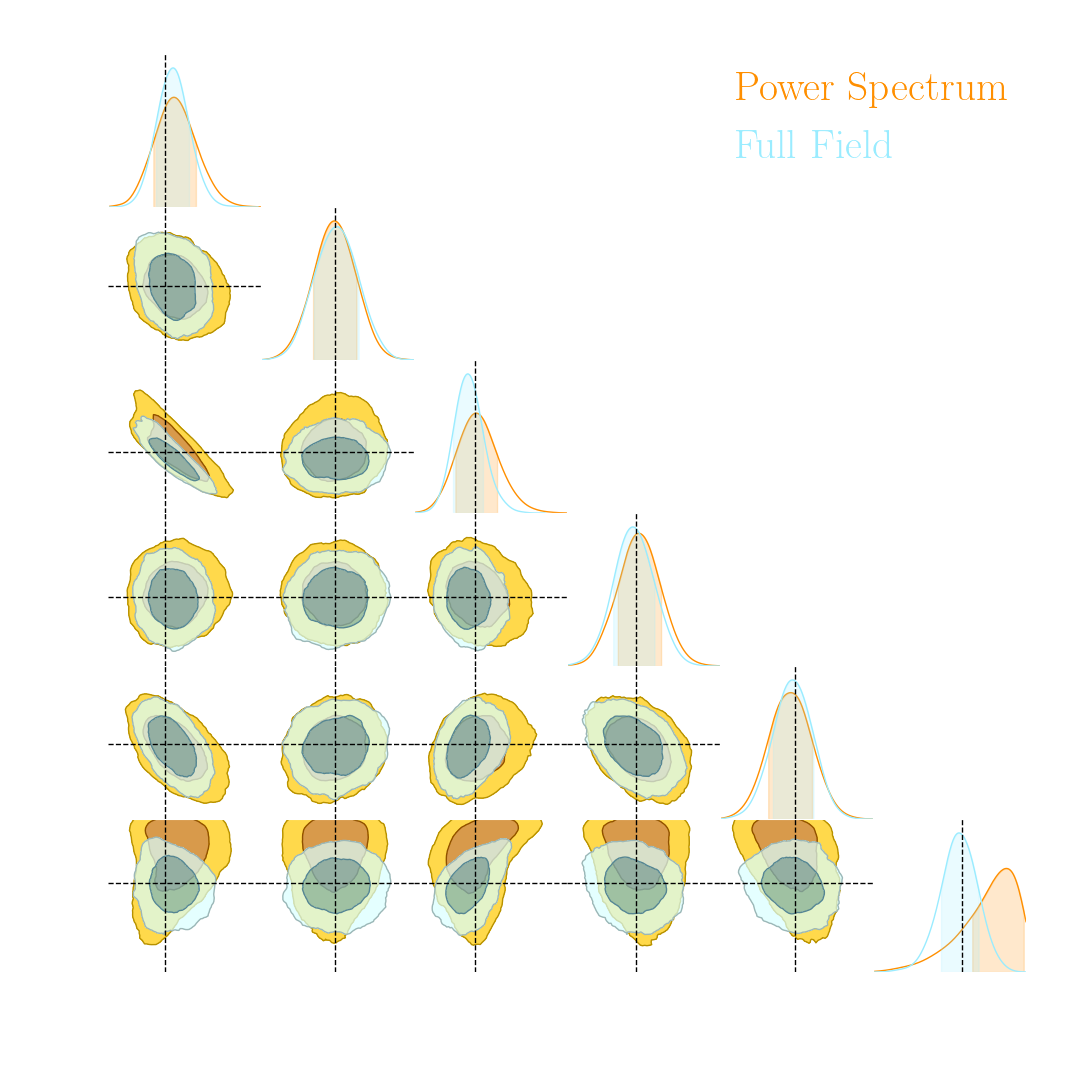


but explicit inference yields intermediate data products

simulated observed data
posterior samples $\kappa = f(z,\theta)$ with $z \sim p(z, \theta | x)$
and not all neural compression techniques are equivalent
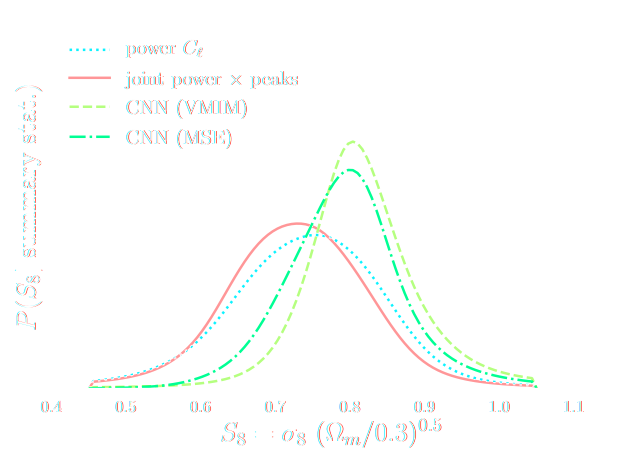
- Most papers applying neural techniques for inference have used sub-optimal compression techniques, e.g. Mean Square Error $$ \mathcal{L} = || f_\varphi(x) - \theta ||_2^2 $$ $\Longrightarrow$ This is ok, contours will simply be larger than they could be.
- A lot of papers are still relying on assuming a proxy Gaussian likelihoods, i.e. estimating a mean and covariance from
simulations.
$\Longrightarrow$ This is dangerous, can lead to biased contours.
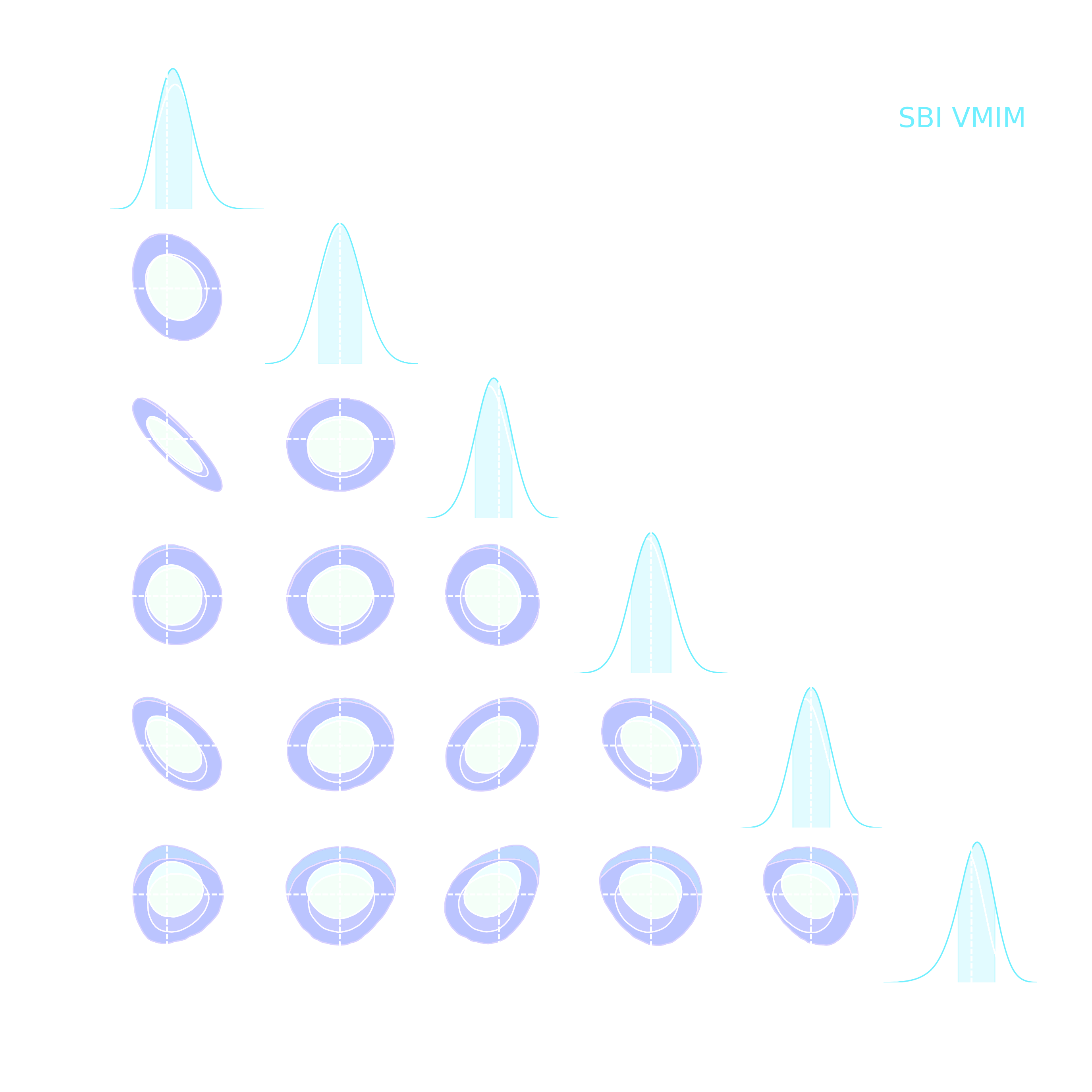
Explicit Inference
Automatically Differentiable Physics
Simulators as Hierarchical Bayesian Models

- If we have access to all latent variables $z$ of the simulator, then the joint log likelihood $p(x | z, \theta)$ is explicit.
- We need to infer the joint posterior $p(\theta, z | x)$ before marginalization to
yield $p(\theta | x) = \int p(\theta, z | x) dz$.
$\Longrightarrow$ Extremely difficult problem as $z$ is typically very high-dimensional. - Necessitates inference strategies with access to gradients of the likelihood. $$\frac{d \log p(x | z, \theta)}{d \theta} \quad ; \quad \frac{d \log p(x | z, \theta)}{d z} $$ For instance: Maximum A Posterior estimation, Hamiltonian Monte-Carlo, Variational Inference.
$\Longrightarrow$ The only hope for explicit cosmological inference is to have fully-differentiable cosmological simulations!
the hammer behind the Deep Learning revolution: Automatic Differentation
- Automatic differentiation allows you to compute analytic derivatives of arbitraty expressions:
If I form the expression $y = a * x + b$, it is separated in fundamental ops: $$ y = u + b \qquad u = a * x $$ then gradients can be obtained by the chain rule: $$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \frac{ \partial u}{\partial x} = 1 \times a = a$$ - This is a fundamental tool in Machine Learning, and autodiff frameworks include TensorFlow and PyTorch.
Enters JAX: NumPy + Autograd + GPU
- JAX follows the NumPy api!
import jax.numpy as np - Arbitrary order derivatives
- Accelerated execution on GPU and TPU

jax-cosmo: Finally a differentiable cosmology library, and it's in JAX!

import jax.numpy as np
import jax_cosmo as jc
# Defining a Cosmology
cosmo = jc.Planck15()
# Define a redshift distribution with smail_nz(a, b, z0)
nz = jc.redshift.smail_nz(1., 2., 1.)
# Build a lensing tracer with a single redshift bin
probe = probes.WeakLensing([nz])
# Compute angular Cls for some ell
ell = np.logspace(0.1,3)
cls = angular_cl(cosmo_jax, ell, [probe])
Current main features
- Weak Lensing and Number counts probes
- Eisenstein & Hu (1998) power spectrum + halofit
- Angular $C_\ell$ under Limber approximation
$\Longrightarrow$ 3x2pt DES Y1 capable
let's compute a Fisher matrix
$$F = - \mathbb{E}_{p(x | \theta)}[ H_\theta(\log p(x| \theta)) ] $$
import jax
import jax.numpy as np
import jax_cosmo as jc
# .... define probes, and load a data vector
def gaussian_likelihood( theta ):
# Build the cosmology for given parameters
cosmo = jc.Planck15(Omega_c=theta[0], sigma8=theta[1])
# Compute mean and covariance
mu, cov = jc.angular_cl.gaussian_cl_covariance_and_mean(cosmo,
ell, probes)
# returns likelihood of data under model
return jc.likelihood.gaussian_likelihood(data, mu, cov)
# Fisher matrix in just one line:
F = - jax.hessian(gaussian_likelihood)(theta)
- No derivatives were harmed by finite differences in the computation of this Fisher!
- Only a small additional compute time compared to one forward evaluation of the model
Inference becomes fast and scalable
- Current cosmological MCMC chains take days, and typically require access to large computer clusters.
- Gradients of the log posterior are required for modern efficient and scalable inference techniques:
- Variational Inference
- Hamiltonian Monte-Carlo
- In jax-cosmo, we can trivially obtain exact gradients:
def log_posterior( theta ): return gaussian_likelihood( theta ) + log_prior(theta) score = jax.grad(log_posterior)(theta) - On a DES Y1 analysis, we find convergence in 70,000 samples with vanilla HMC, 140,000 with Metropolis-Hastings
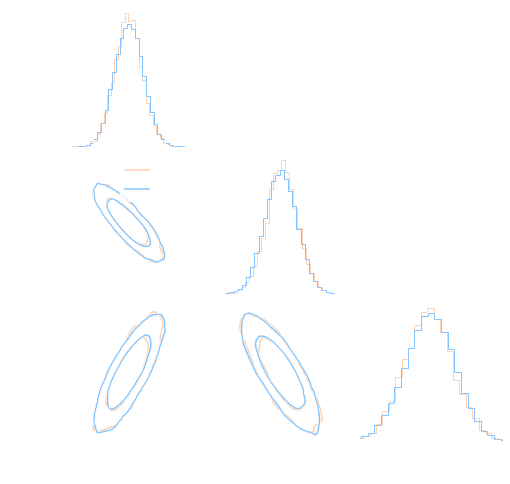
DES Y1 posterior, jax-cosmo HMC vs Cobaya MH
(credit: Joe Zuntz)
Forward Models in Cosmology
 Linear Field
Linear Field
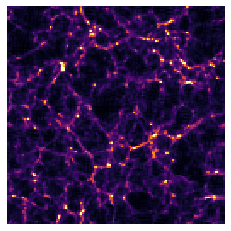 Final Dark Matter
Final Dark Matter
 Dark Matter Halos
Dark Matter Halos
 Galaxies
Galaxies
$\longrightarrow$
N-body simulations
$\longrightarrow$
Group Finding
algorithms
Group Finding
algorithms
$\longrightarrow$
Semi-analytic &
distribution models
Semi-analytic &
distribution models
the Fast Particle-Mesh scheme for N-body simulations
The idea: approximate gravitational forces by estimating densities on a grid.- The numerical scheme:
- Estimate the density of particles on a mesh
=> compute gravitational forces by FFT - Interpolate forces at particle positions
- Update particle velocity and positions, and iterate
- Estimate the density of particles on a mesh
- Fast and simple, at the cost of approximating short range interactions.

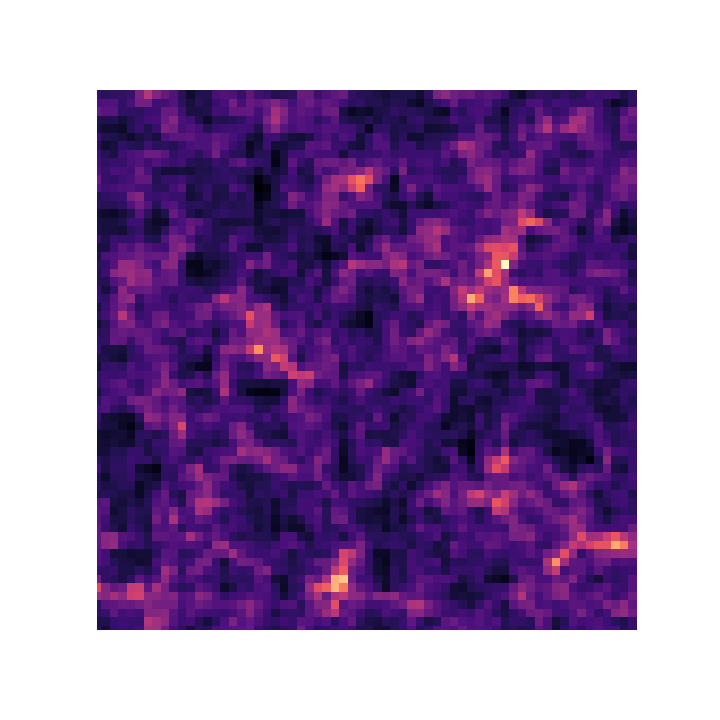


$\Longrightarrow$ Only a series of FFTs and interpolations.
introducing FlowPM: Particle-Mesh Simulations in TensorFlow


import tensorflow as tf
import flowpm
# Defines integration steps
stages = np.linspace(0.1, 1.0, 10, endpoint=True)
initial_conds = flowpm.linear_field(32, # size of the cube
100, # Physical size
ipklin, # Initial powerspectrum
batch_size=16)
# Sample particles and displace them by LPT
state = flowpm.lpt_init(initial_conds, a0=0.1)
# Evolve particles down to z=0
final_state = flowpm.nbody(state, stages, 32)
# Retrieve final density field
final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions),
final_state[0])
- Seamless interfacing with deep learning components
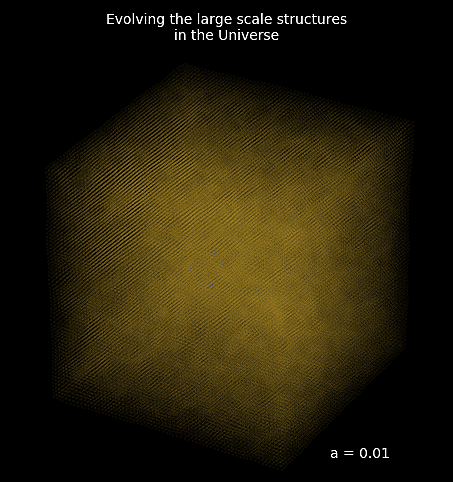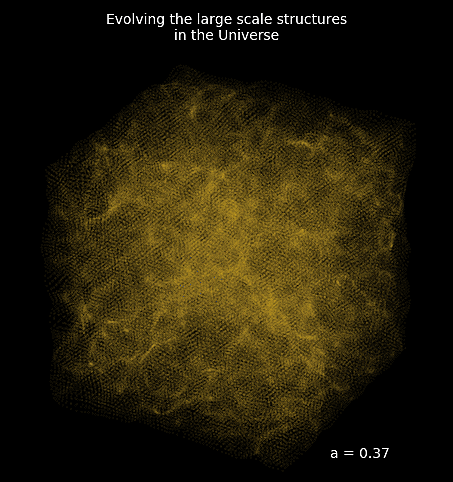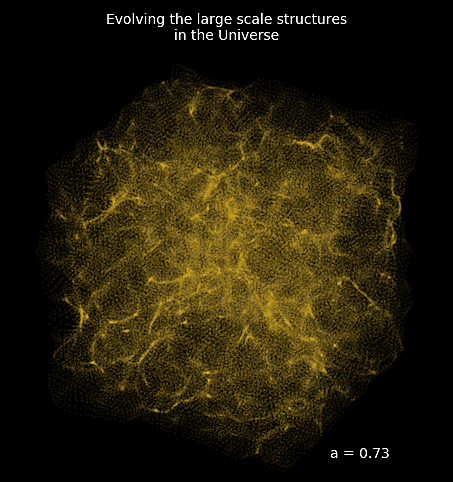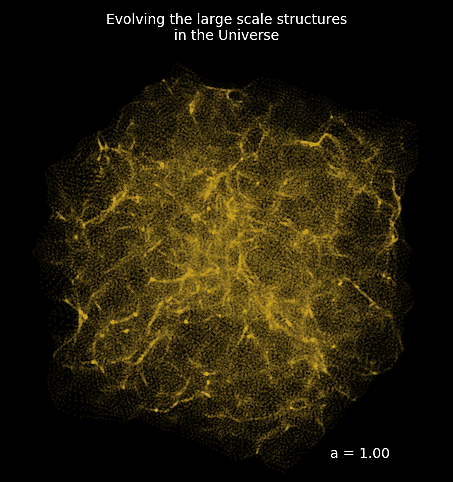
Mesh FlowPM: distributed, GPU-accelerated, and automatically differentiable simulations

- We developed a Mesh TensorFlow implementation that can scale on GPU clusters (horovod+NCCL).
- For a $2048^3$ simulation:
- Distributed on 256 NVIDIA V100 GPUs
- Don't hesitate to reach out if you have a use case for model parallelism!
![]()
- Now developing the next generation of these tools in JAX
Hybrid Physical-Neural ODEs for Fast N-body Simulations


Work in collaboration with:
Denise Lanzieri
$\Longrightarrow$ Learn residuals to known physical equations to improve accuracy of fast PM simulations.
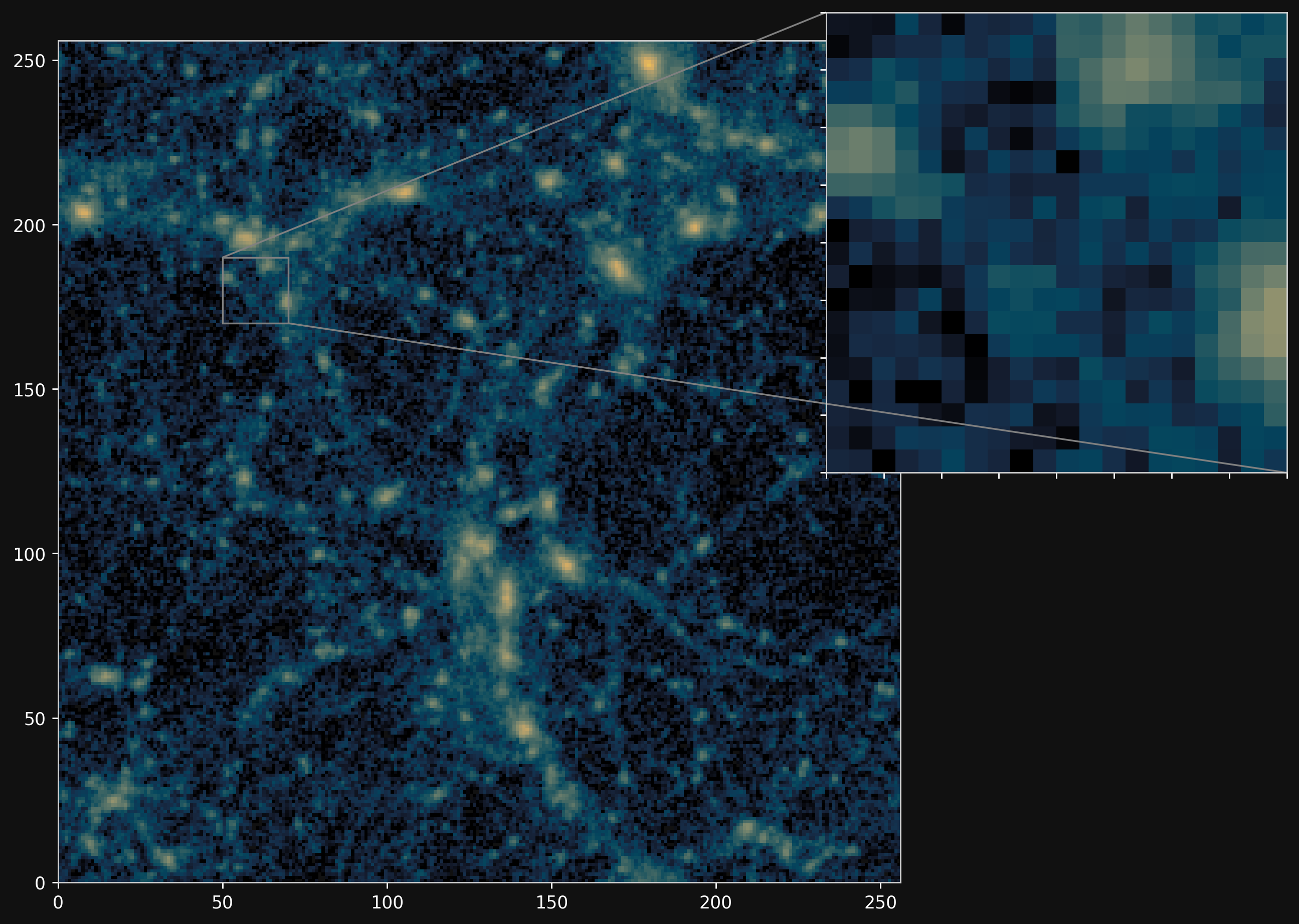
Fill the gap in the accuracy-speed space of PM simulations
Camels simulations
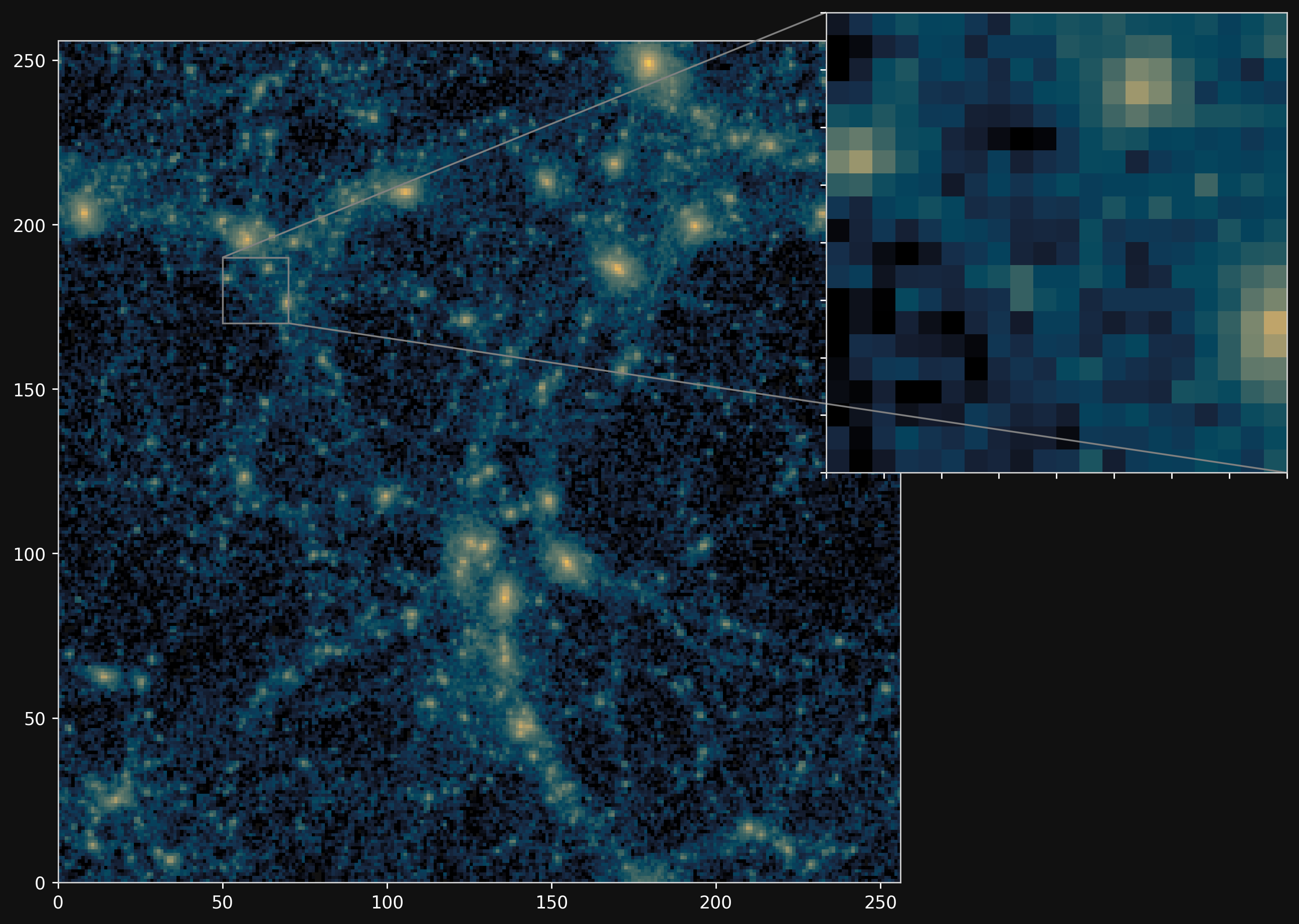
PM simulations
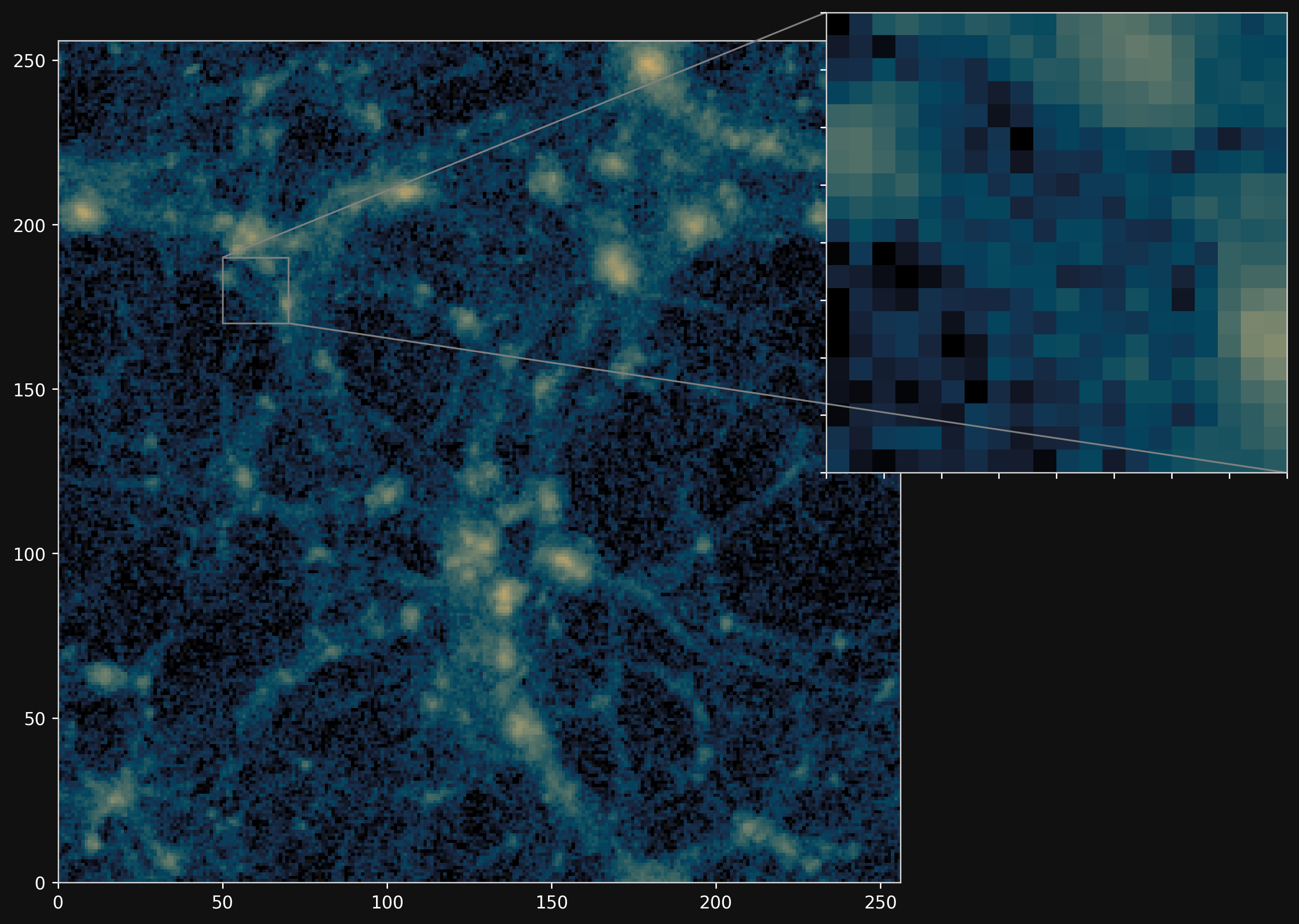
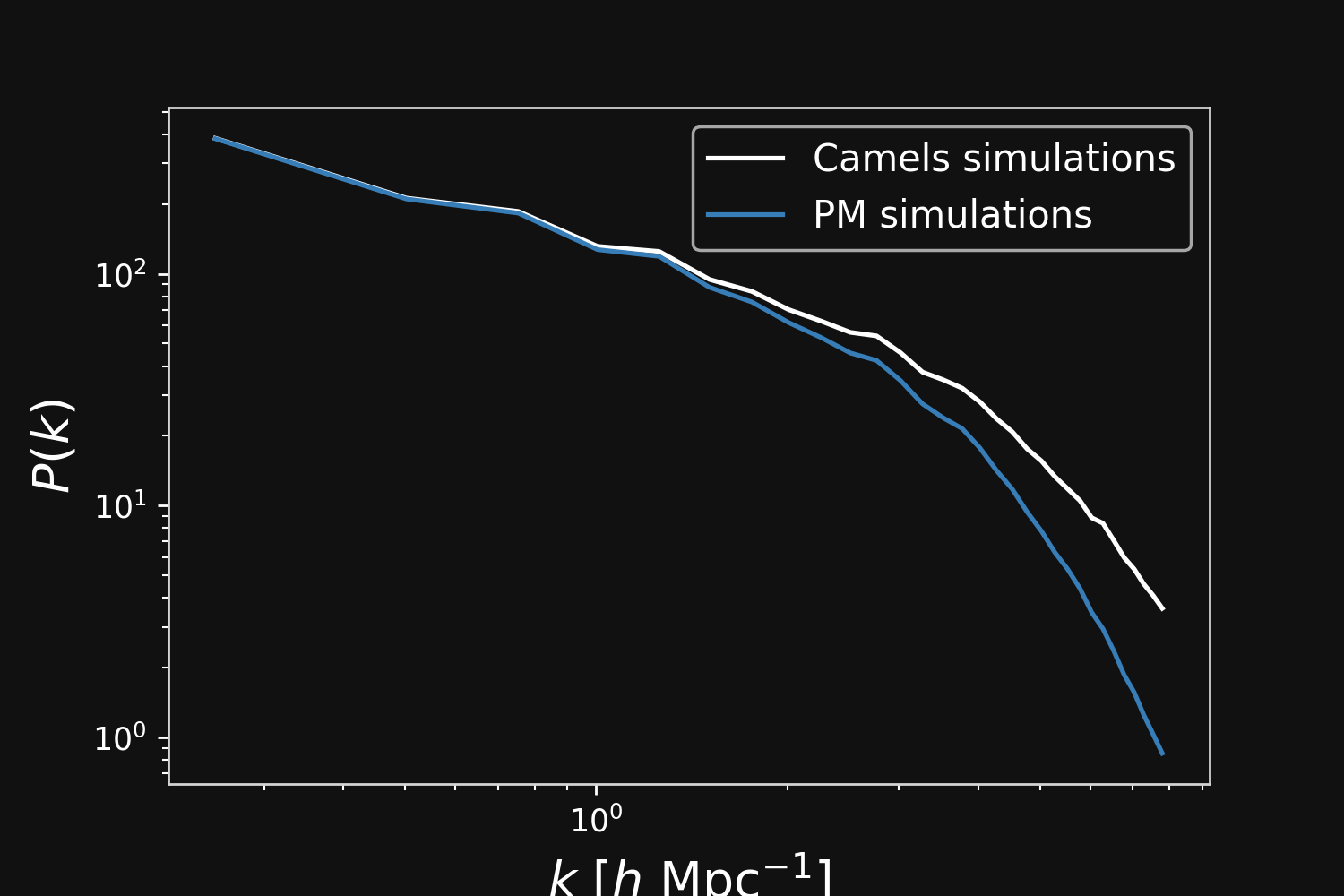
Hybrid physical/neural differential equations
$$\left\{ \begin{array}{ll} \frac{d \color{#6699CC}{\mathbf{x}} }{d a} & = \frac{1}{a^3 E(a)} \color{#6699CC}{\mathbf{v}} \\ \frac{d \color{#6699CC}{\mathbf{v}}}{d a} & = \frac{1}{a^2 E(a)} F_\theta( \color{#6699CC}{\mathbf{x}} , a), \\ F_\theta( \color{#6699CC}{\mathbf{x}}, a) &= \frac{3 \Omega_m}{2} \nabla \left[ \color{#669900}{\phi_{PM}} (\color{#6699CC}{\mathbf{x}}) \right] \end{array} \right. $$- $\mathbf{x}$ and $\mathbf{v}$ define the position and the velocity of the particles
- $\phi_{PM}$ is the gravitational potential in the mesh
$\to$ We can use this parametrisation to complement the physical ODE with neural networks.
$$F_\theta(\mathbf{x}, a) = \frac{3 \Omega_m}{2} \nabla \left[ \phi_{PM} (\mathbf{x}) \ast \mathcal{F}^{-1} (1 + \color{#996699}{f_\theta(a,|\mathbf{k}|)}) \right] $$
Correction integrated as a Fourier-based isotropic filter $f_{\theta}$ $\to$ incorporates translation and rotation symmetries
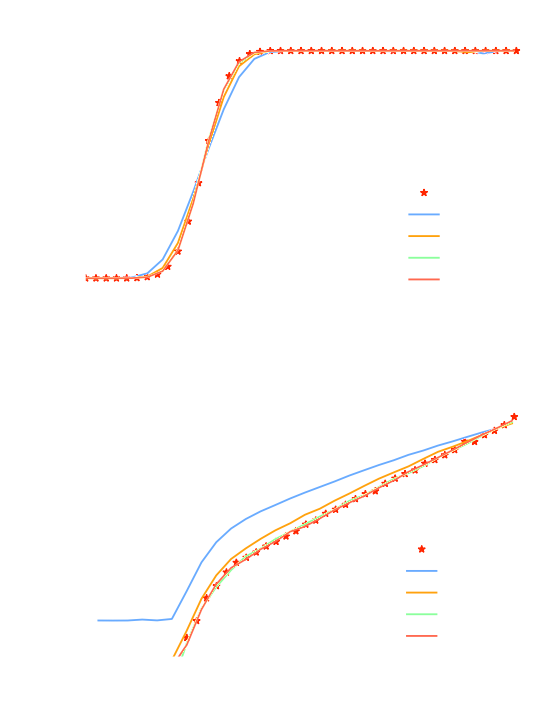
Projections of final density field
Camels simulations
![]()

PM simulations
![]()

PM+NN correction
![]()

Results
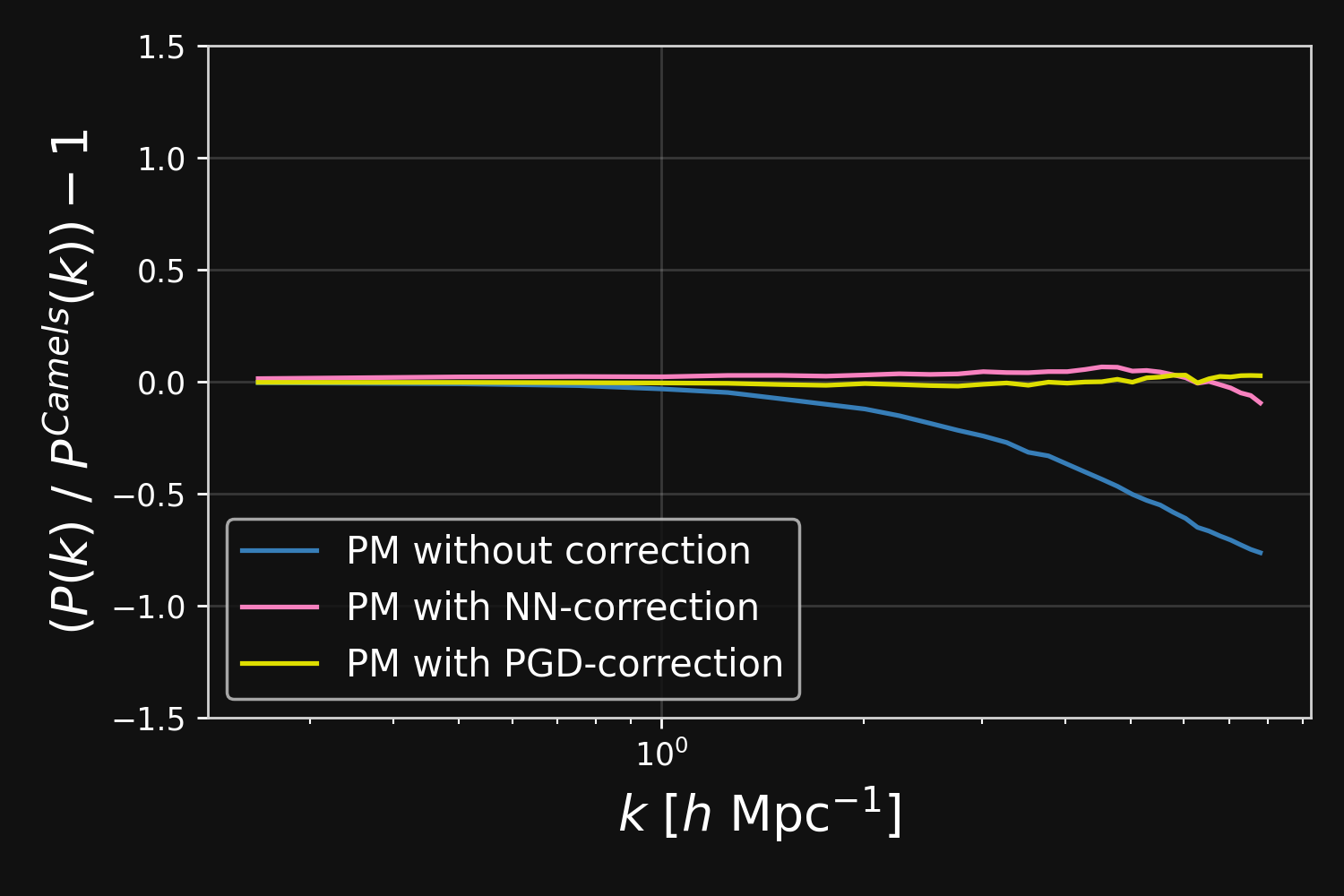
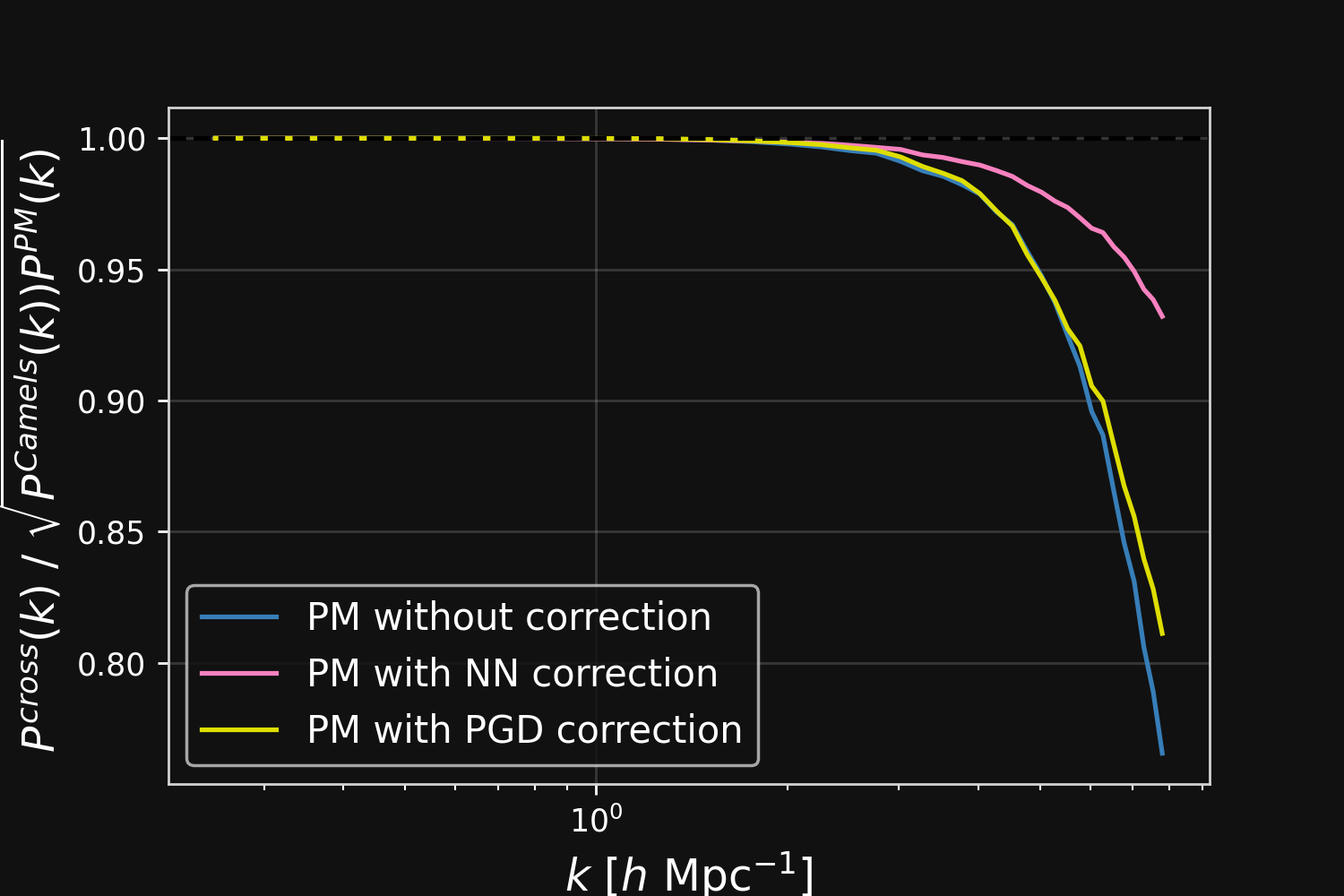
Forward Models in Cosmology
 Linear Field
Linear Field
 Final Dark Matter
Final Dark Matter
 Dark Matter Halos
Dark Matter Halos
 Galaxies
Galaxies
$\longrightarrow$
N-body simulations
$\longrightarrow$
Group Finding
algorithms
Group Finding
algorithms
$\longrightarrow$
HOD models
HOD models
Differentiable sampling from Halo Occupation Distributions

https://github.com/DifferentiableUniverseInitiative/DHOD
- Sampling from a discrete random distribution is classically not a differentiable operation
- Relaxed and reparameterized HOD sampling
- Relaxed Bernoulli distributions for centrals
$$ N_{\rm cen} = \frac{1}{1 + \exp( - (\log(\frac{p}{1 - p}) + \epsilon)/\tau) } \mbox{ with } \epsilon \sim \mathrm{Logistic}(0,1) \;. $$ where $\tau$ is a temperature parameter - Relaxed Binomial distribution for satelittes
$$ N_{\rm sat} \sim \mathrm{Binomial}\left(N, p=\frac{ \left\langle N_{\rm sat}\right\rangle }{N} \right)$$
- Relaxed Bernoulli distributions for centrals
Conclusion
Conclusion
Merging Deep Learning with Physical Models for Bayesian Inference
$\Longrightarrow$ Makes Bayesian inference possible at scale and with non-trivial models!
- Complement known physical models with data-driven components
- Use data-driven generative model as prior for solving inverse problems.
- Enables inference in high dimension from numerical simulators.
- Automagically construct summary statistics.
- Provides the density estimation tools needed.
- Differentiable physical models for fast inference
- Differentiability enables Bayesian inference over large scale simulations.
- Models can directly be embedded alongside deep learning components.
Thank you !