Merging Physical Models with Deep Learning for Cosmology
Learning to Discover, April 29th 2022
François Lanusse



slides at eiffl.github.io/Learning2022
the $\Lambda$CDM view of the Universe



the Rubin Observatory Legacy Survey of Space and Time
- 1000 images each night, 15 TB/night for 10 years
- 18,000 square degrees, observed once every few days
- Tens of billions of objects, each one observed $\sim1000$ times
Previous generation survey: SDSS
Image credit: Peter Melchior
Current generation survey: DES
Image credit: Peter Melchior
LSST precursor survey: HSC
Image credit: Peter Melchior
Can AI solve all of our problems?
Branched GAN model for deblending (Reiman & Göhre, 2018)
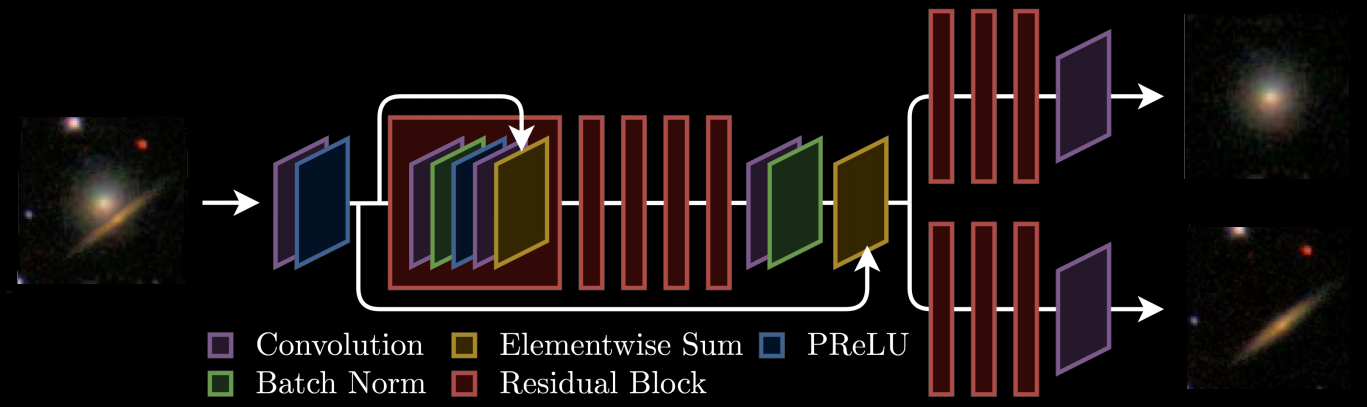
The issue with using deep learning as a black-box
- No explicit control of noise, PSF, number of sources.
- Model would have to be retrained for all observing configurations
- No guarantees on the network output (e.g. flux preservation, artifacts)
- No proper uncertainty quantification.

Focus of this talk
This talk
Generic approach to uncertainty quantification and interpretability:
- (Differentiable) Physical Forward Models
- Deep Generative Models
- Bayesian Inference
Data-driven priors for astronomical inverse problems
A Motivating Example: Deconvolution

Hubble Space Telescope
some deep neural network

Simulated Ground-Based Telescope
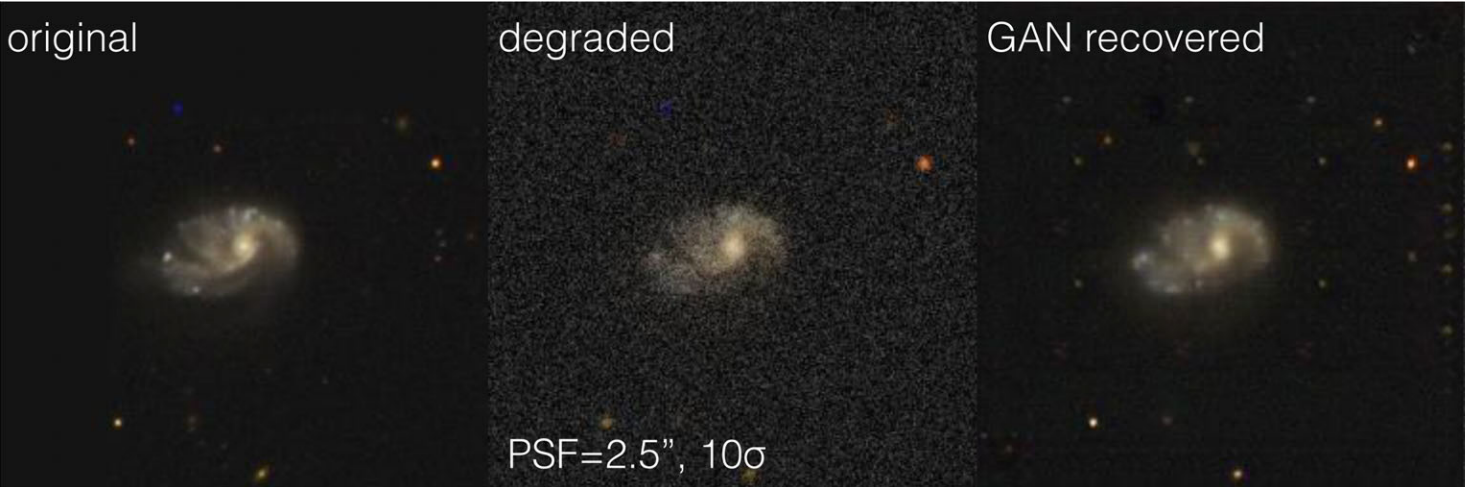
(Schawinski, et al. 2017)
A Physicist's approach: let's build a model





$\longrightarrow$
$g_\theta$
$g_\theta$
$\longrightarrow$
PSF
PSF
$\longrightarrow$
Pixelation
Pixelation
$\longrightarrow$
Noise
Noise


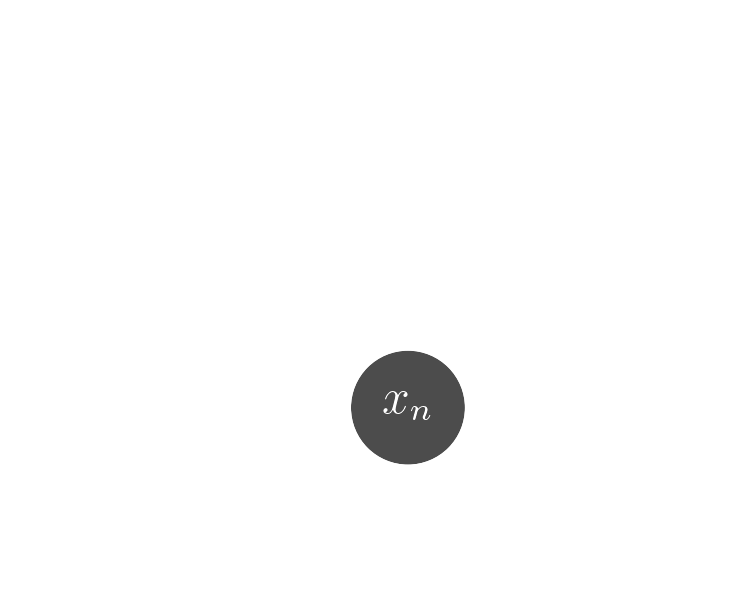
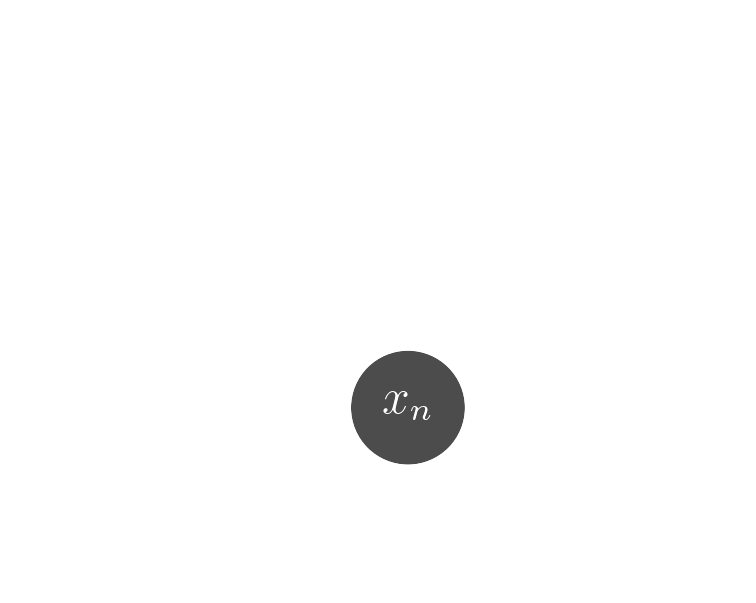
Probabilistic model
$$ x \sim ? $$
$$ x \sim \mathcal{N}(z, \Sigma) \quad z \sim ? $$
latent $z$ is a denoised galaxy image
latent $z$ is a denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} z, \Sigma) \quad z \sim ?$$
latent $z$ is a super-resolved and denoised galaxy image
latent $z$ is a super-resolved and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast z), \Sigma) \quad z \sim ? $$
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
latent $z$ is a deconvolved, super-resolved, and denoised galaxy image
$$ x \sim \mathcal{N}( \mathbf{P} (\Pi \ast g_\theta(z)), \Sigma) \quad z \sim \mathcal{N}(0, \mathbf{I}) $$
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
latent $z$ is a Gaussian sample
$\theta$ are parameters of the model
$\Longrightarrow$ Decouples the morphology model from the observing conditions.
Bayesian Inference a.k.a. Uncertainty Quantification
The Bayesian view of the problem:
$$ p(z | x ) \propto p_\theta(x | z, \Sigma, \mathbf{\Pi}) p(z)$$
where:
- $p( z | x )$ is the posterior
- $p( x | z )$ is the data likelihood, contains the physics
- $p( z )$ is the prior


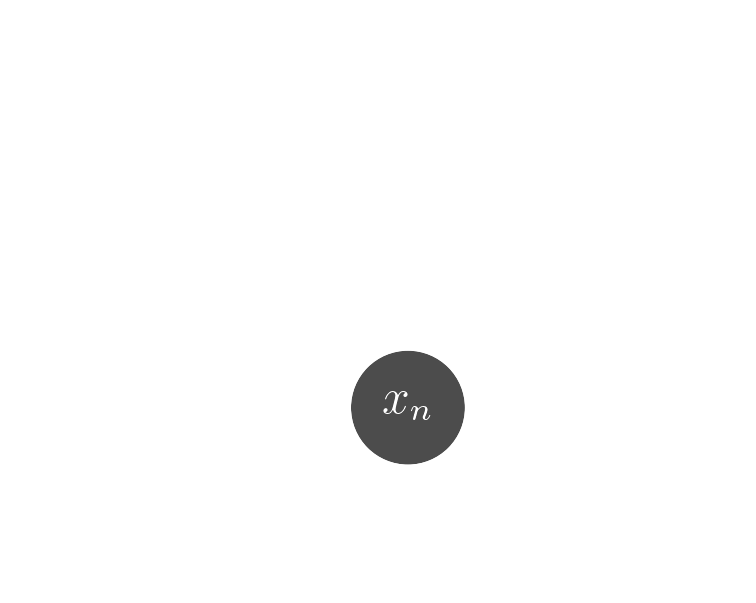
Data
$x_n$
$x_n$
Truth
$x_0$
$x_0$
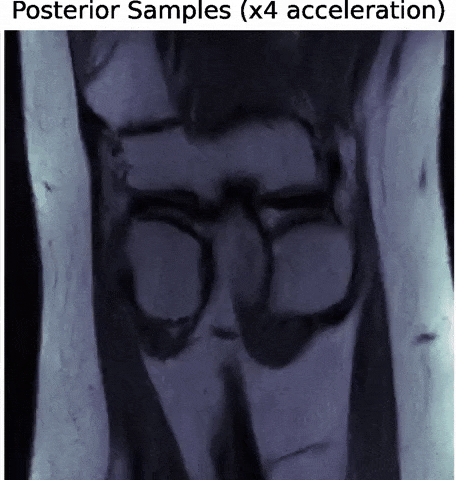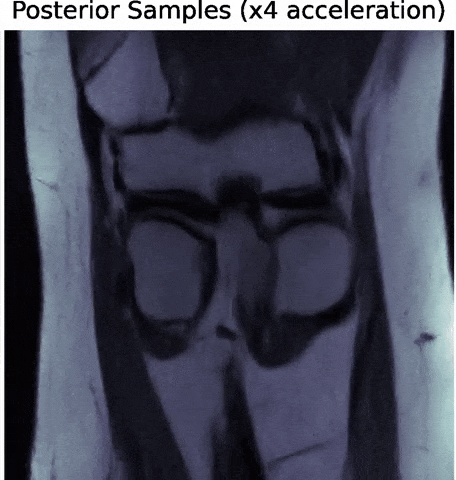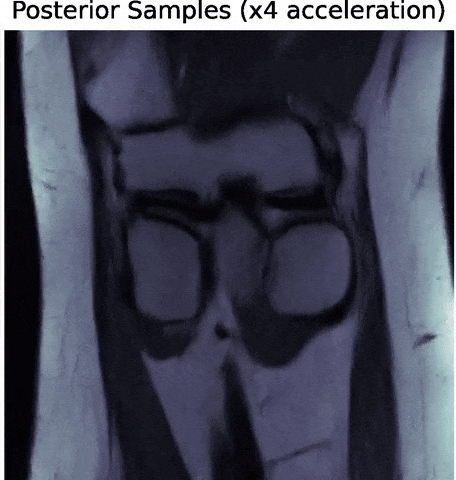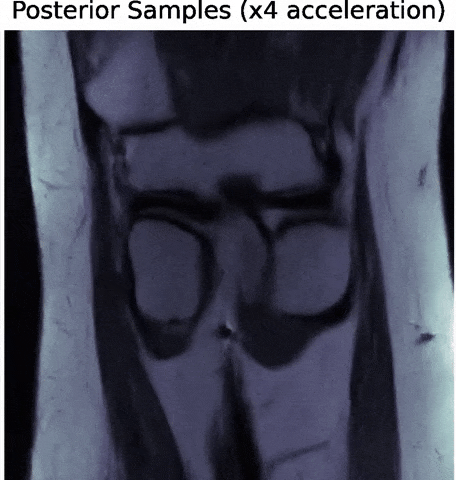
Posterior samples
$g_\theta(z)$
$g_\theta(z)$

$\mathbf{P} (\Pi \ast g_\theta(z))$
Median

Data residuals
$x_n - \mathbf{P} (\Pi \ast g_\theta(z))$
$x_n - \mathbf{P} (\Pi \ast g_\theta(z))$
Standard Deviation
$\Longrightarrow$ Uncertainties are fully captured by the posterior.
How do you do this in practice?
How to train your model from corrupted data
- Training the model amounts to finding $\theta_\star$ that
maximizes the marginal likelihood of the model:
$$p_\theta(x | \Sigma, \Pi) = \int \mathcal{N}( \mathbf{P}(\Pi \ast g_\theta(z)), \Sigma) \ p(z) \ dz$$
$\Longrightarrow$ This is classically intractable
- Efficient training of parameters $\theta$ can be achieved by:
- Adversarial Learning
- Amortized Variational Inference
Auto-Encoding Variational Bayes (Kingma & Welling, 2014)
- We introduce a parametric distribution $q_\phi(z | x, \Pi, \Sigma)$ which aims to model the posterior $p_{\theta}(z | x, \Pi, \Sigma)$.
- Working out the KL divergence between these two distributions leads to: $$\log p_\theta(x | \Sigma, \Pi) \quad \geq \quad - \mathbb{D}_{KL}\left( q_\phi(z | x, \Sigma, \Pi) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}(. | x, \Sigma, \Pi)} \left[ \log p_\theta(x | z, \Sigma, \Pi) \right]$$ $\Longrightarrow$ Evidence Lower-Bound: differentiable with respect to $\theta$ and $\phi$.
Flow-VAE samples

How to perform efficient posterior inference?



- Posterior fitting by Variational Inference
$$ \mathrm{ELBO} = - \mathbb{D}_{KL}\left( q_\phi(z) \parallel p(z) \right) \quad + \quad \mathbb{E}_{z \sim q_{\phi}} \left[ \log p_\theta(x_n | z, \Sigma_n, \Pi_n) \right]$$ - Posterior fitting by $EL_{2}O$
$$EL_2O = \arg \min_\theta \mathbb{E}_{z \sim p^{\prime}} \sum_i \alpha_i \parallel \nabla_{z}^n \ln q_\theta(z) - \nabla_{z}^{n} \ln p(z | x_n, \Sigma_n, \Pi_n) \parallel_2^2$$See (Seljak & Yu, 2019) for more details. - Or your favorite method...
Other examples of applications of deep data-driven priors
Simulation-Based Inference
by Neural Summarisation and Density Estimation

Work in collaboration with Niall Jeffrey, Justin Alsing


$\Longrightarrow$ Learn an implicit data likelihood from simulations.
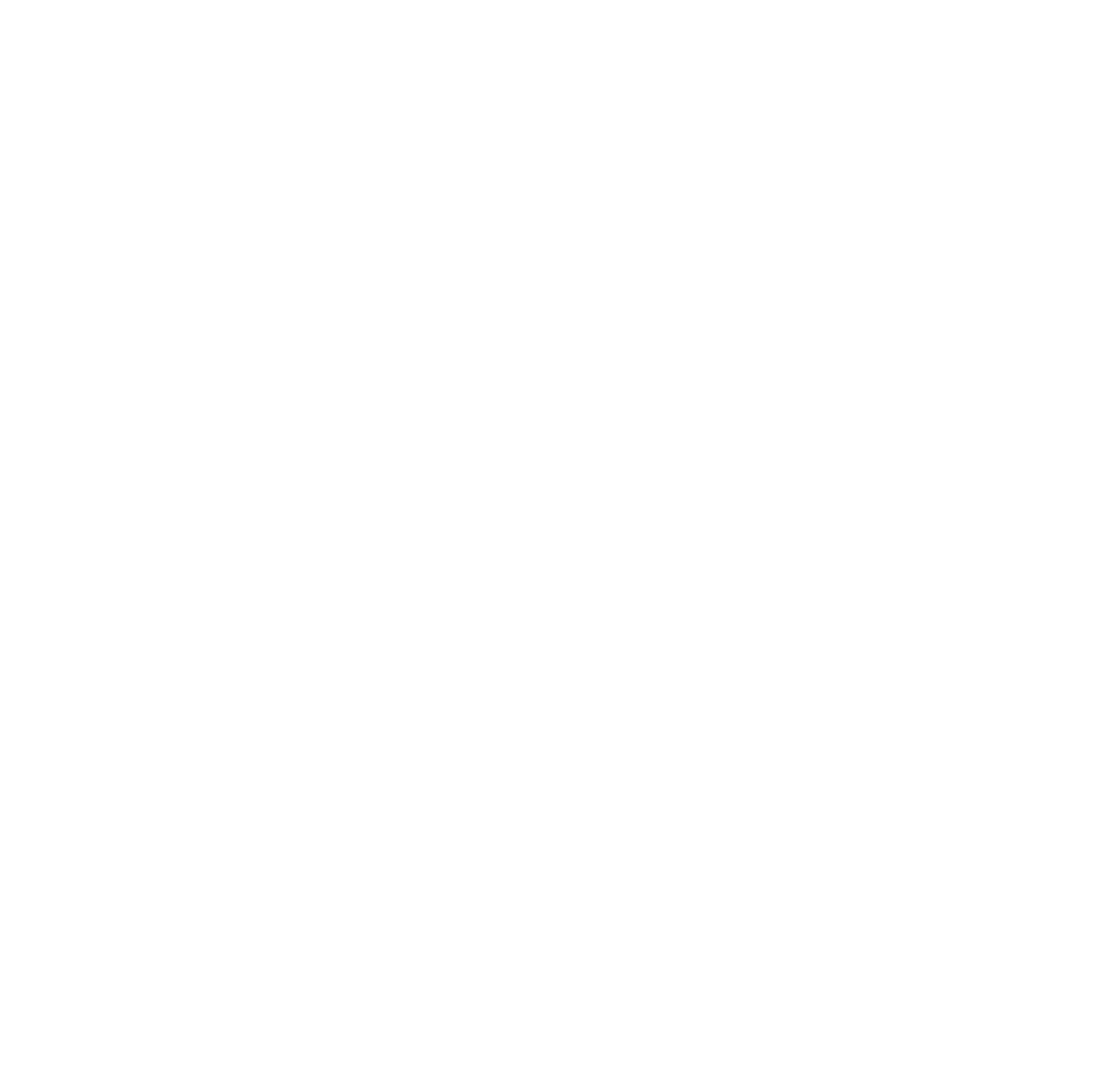
limits of traditional cosmological inference
HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
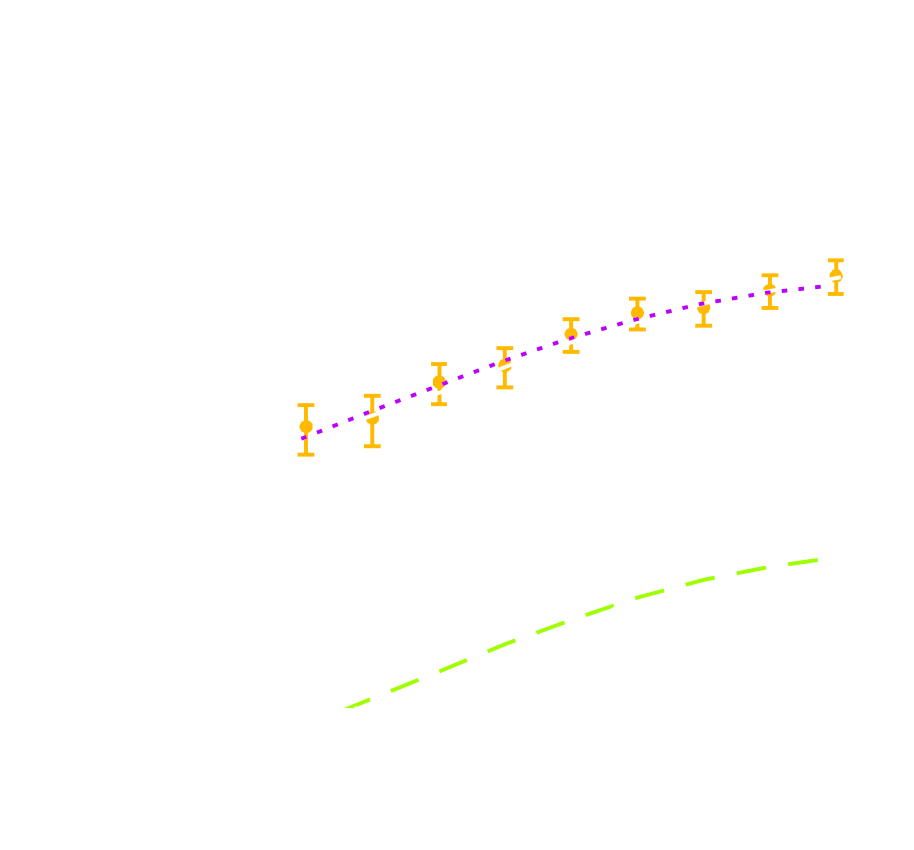
(Hikage et al. 2018)
- Measure the ellipticity $\epsilon = \epsilon_i + \gamma$ of all galaxies
$\Longrightarrow$ Noisy tracer of the weak lensing shear $\gamma$ - Compute summary statistics based on 2pt functions,
e.g. the power spectrum - Run an MCMC to recover a posterior on model parameters, using an analytic likelihood $$ p(\theta | x ) \propto \underbrace{p(x | \theta)}_{\mathrm{likelihood}} \ \underbrace{p(\theta)}_{\mathrm{prior}}$$
Main limitation: the need for an explicit likelihood
We can only compute the likelihood for simple summary statistics and on large scales
$\Longrightarrow$ We are dismissing a large amount of information!
A different road: forward modeling
- Instead of trying to analytically evaluate the likelihood, let us build a forward model of the observables.
$\Longrightarrow$ Learn an implicit likelihood $p(x|\theta)$ given by the simulator as our physical model
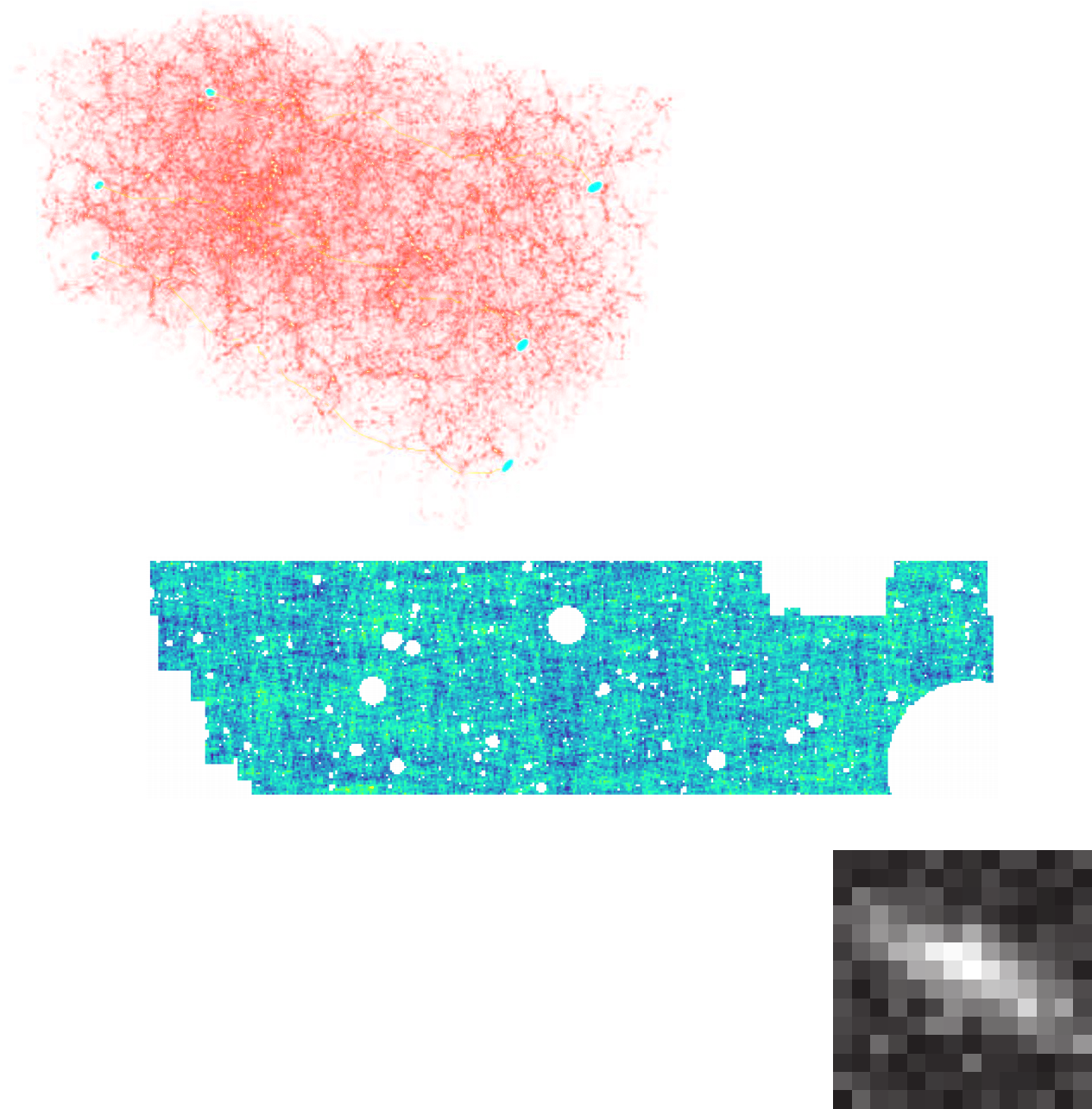
End-to-end framework for likelihood-free parameter inference with DES SV

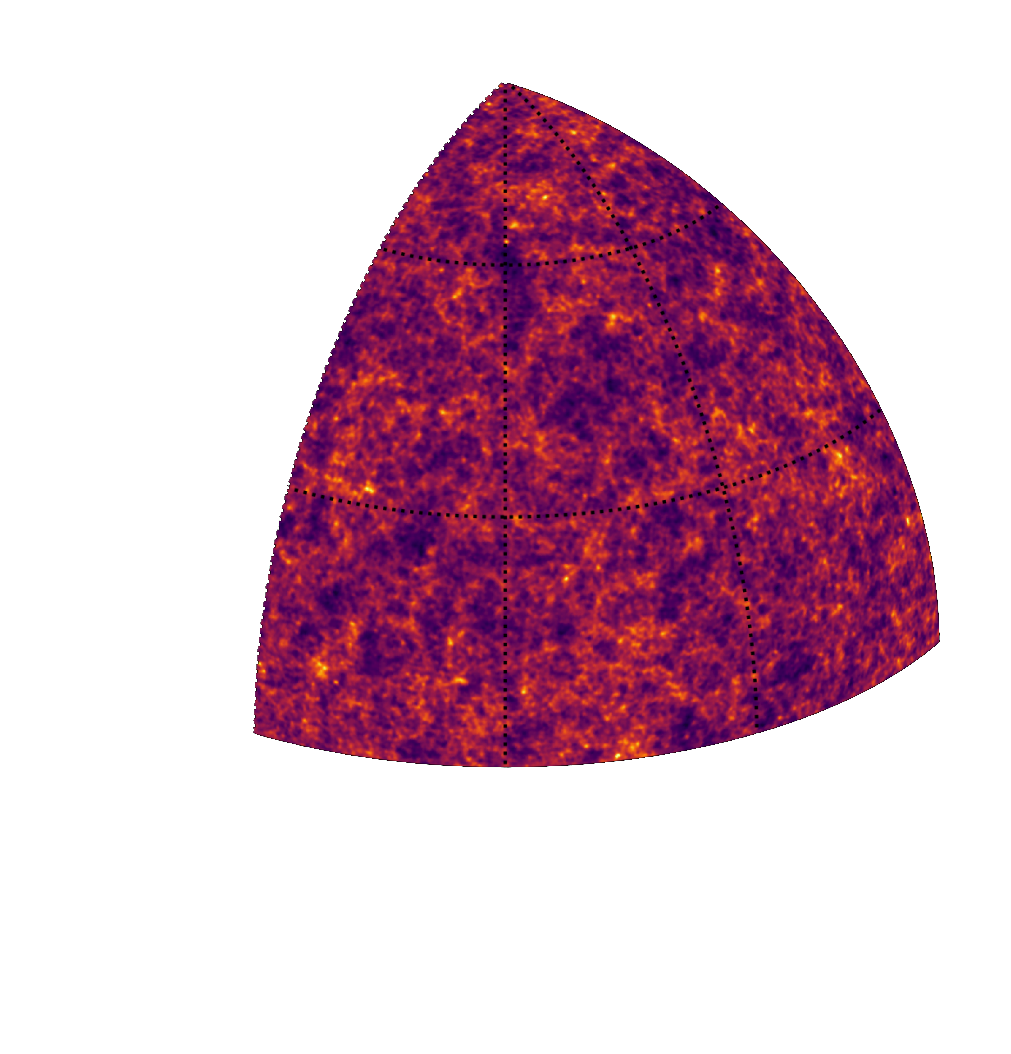
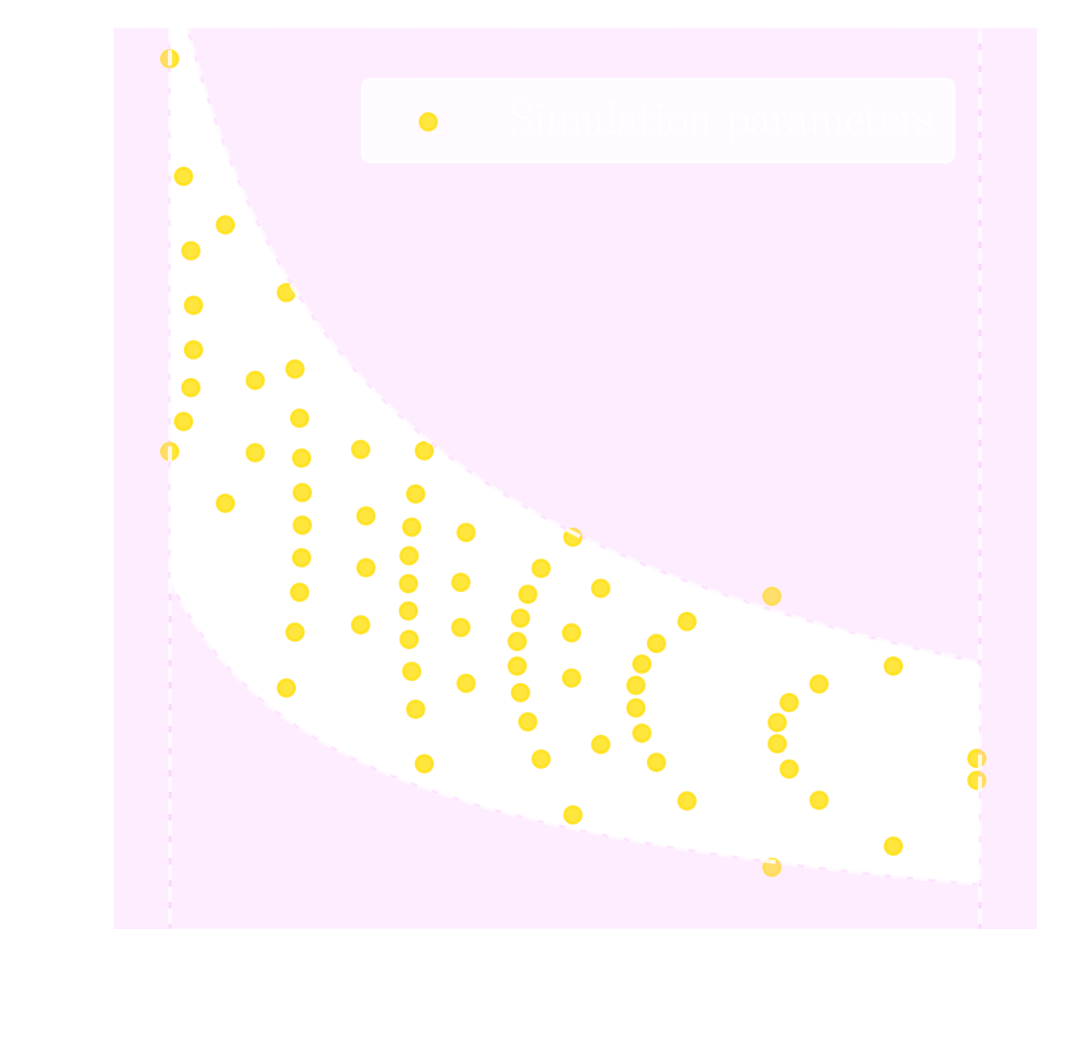
Suite of N-body + raytracing simulations: $\mathcal{D}$
Our strategy
A two-steps approach to inference
- Automatically learn an optimal low-dimensional summary statistic $$y = f_\varphi(\kappa_{KS}) $$
- Use Neural Density Estimation to build an estimate $p_\phi$ of the likelihood function $p(y \ | \ \theta)$ (Neural Likelihood Estimation)
- Run a conventional Markov Chain Monte Carlo sampling
Learning summary statistics by Variational Mutual Information Maximization
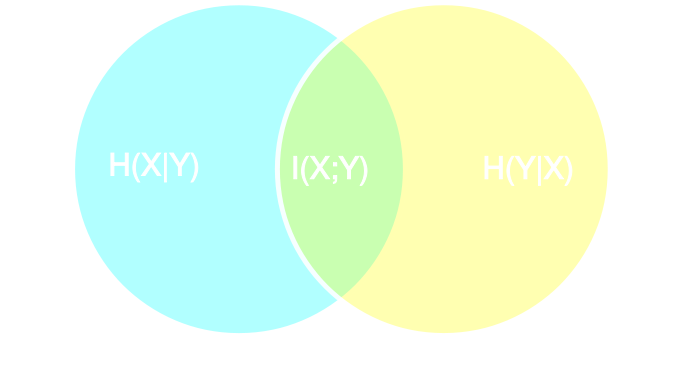
- Mutual information between $X$ and $Y$:
“"amount of information" obtained about one random variable through observing the other random variable”
- Given a parametric summarizing function $y = f_\phi(\kappa(\theta))$ optimizing $f_\phi$ can be done by maximizing $I(y, \theta)$.
- In practice, $f_\phi$ is a CNN, trained to maximize a variational lower bound on the mutual information: $$ I(y ; \theta) \ \ge \ \mathbb{E}_{y, \theta} [ \log q_\phi(\theta | y) ] + H(\Theta) $$
deep residual networks for lensing maps compression
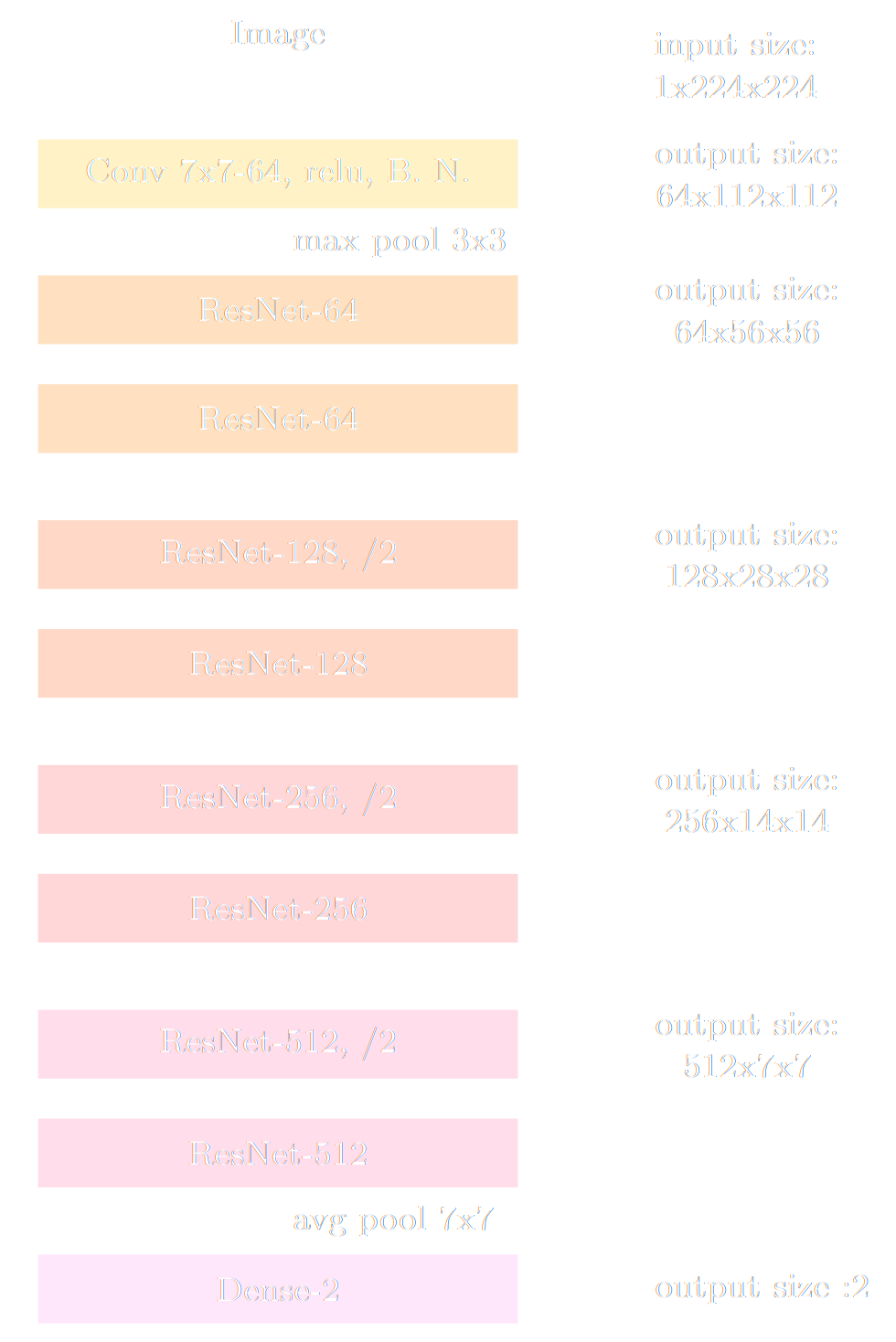
- Deep Residual Network $y = f_\phi(x)$ followed by neural density estimator $q_\phi(\theta | y)$
- Training on weak lensing maps simulated for different cosmologies
- Training by Variational Mutual Information Maximization: $$\mathbb{E}_{(x, \theta) \in \mathcal{D}} [ \log q_\phi(\theta | f_\phi(y) ) ]$$
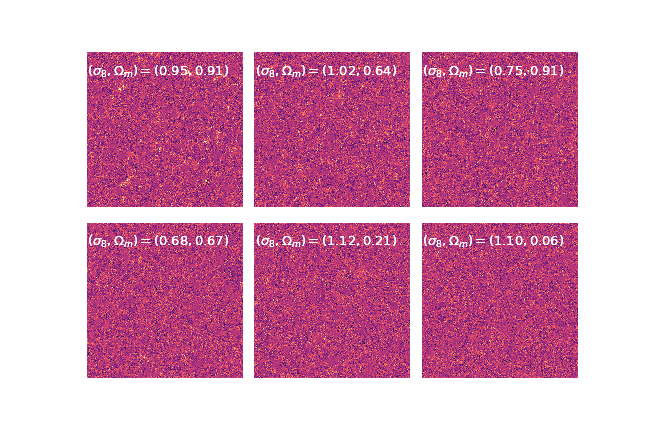


Estimating the likelihood by Neural Density Estimation
$\Longrightarrow$ We cannot assume a Gaussian likelihood for the summary $y = f_\phi(\kappa)$ but we can learn $p(y | \theta)$: Neural Likelihood Estimation.
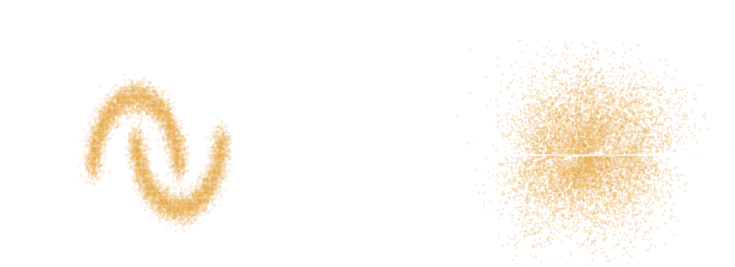
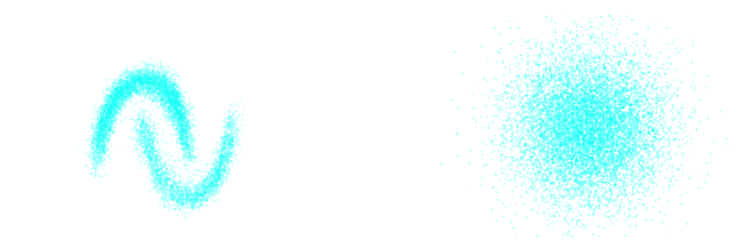
Dinh et al. 2016
Neural Likelihood Estimation by Normalizing Flow
- We use a conditional Normalizing Flow to build an explicit model for the likelihood function $$ \log p_\varphi (y | \theta)$$
- In practice we use the pyDELFI package and an ensemble of NDEs for robustness.
- Once learned, we can use the likelihood as part of a conventional MCMC chain
Parameter constraints from DES SV data
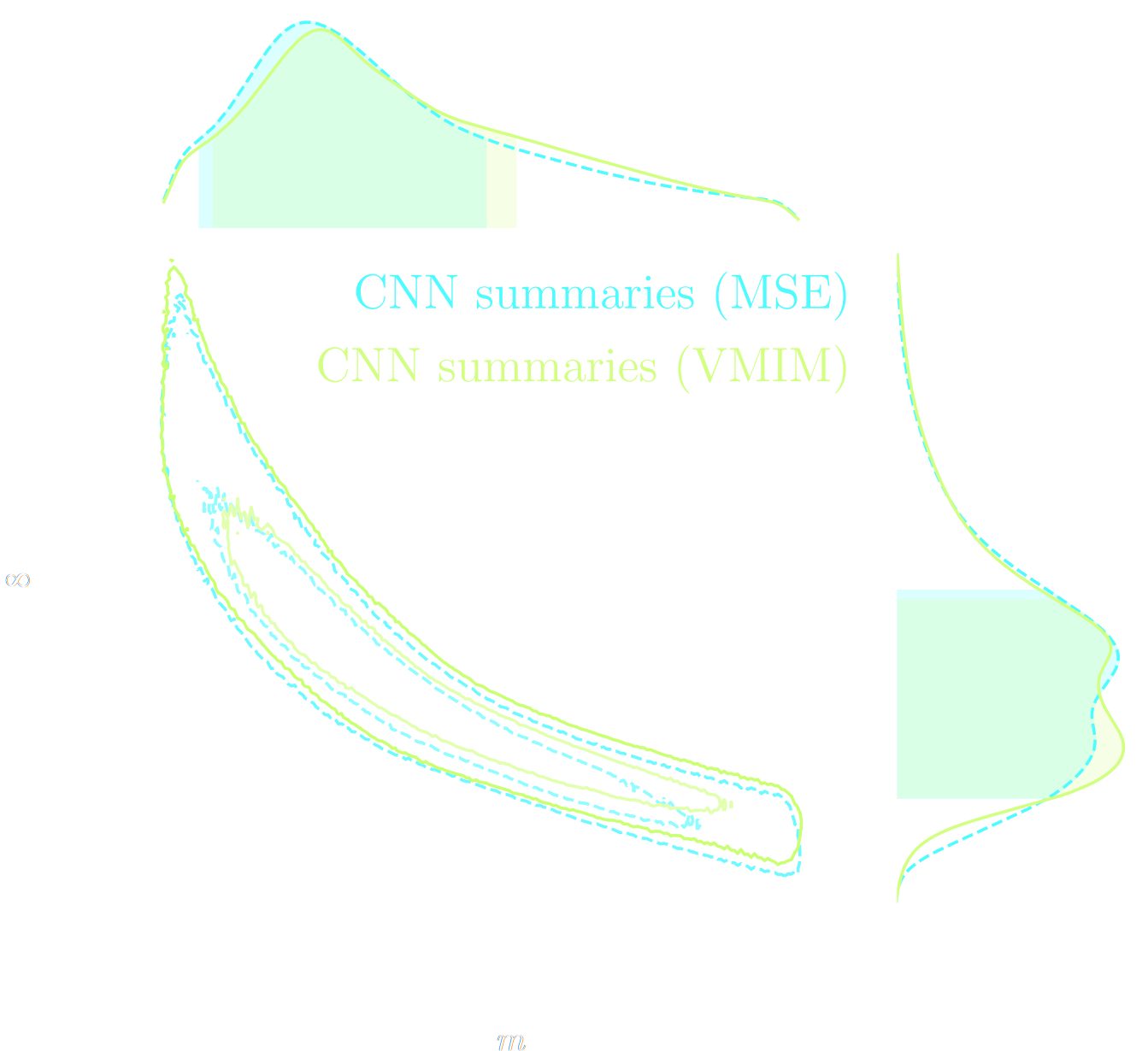
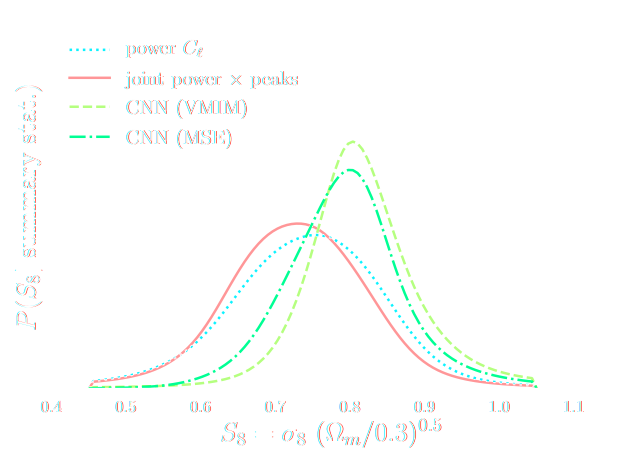
Automatically Differentiable Physics
Back to forward modeling: the Hierarchical Bayesian Inference perspective
- Another approach to using simulations is to consider them as large Hierarchical Bayesian Models.
- Each component of the model is now tractable, but at the cost of a large number of latent variables.
$\Longrightarrow$ How to peform efficient inference in this large number of dimensions?
- A non-exhaustive list of methods:
- Hamiltonian Monte-Carlo
- Variational Inference
- MAP+Laplace
- Gold Mining
- Dimensionality reduction by Fisher-Information Maximization
What do they all have in common?
-> They require fast, accurate, differentiable forward simulations
-> They require fast, accurate, differentiable forward simulations

(Schneider et al. 2015)
How do we simulate the Universe in a fast and differentiable way?
Forward Models in Cosmology
 Linear Field
Linear Field
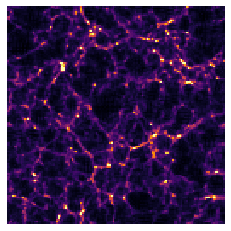 Final Dark Matter
Final Dark Matter
 Dark Matter Halos
Dark Matter Halos
 Galaxies
Galaxies
$\longrightarrow$
N-body simulations
$\longrightarrow$
Group Finding
algorithms
Group Finding
algorithms
$\longrightarrow$
Semi-analytic &
distribution models
Semi-analytic &
distribution models
You can try to learn the simulation...
Learning particle displacement with a UNet. S. He, et al. (2019)

The issue with using deep learning as a black-box
- No guarantees to work outside of training regime.
- No guarantees to capture dependence on cosmology accurately.
the Fast Particle-Mesh scheme for N-body simulations
The idea: approximate gravitational forces by estimating densities on a grid.- The numerical scheme:
- Estimate the density of particles on a mesh
=> compute gravitational forces by FFT - Interpolate forces at particle positions
- Update particle velocity and positions, and iterate
- Estimate the density of particles on a mesh
- Fast and simple, at the cost of approximating short range interactions.

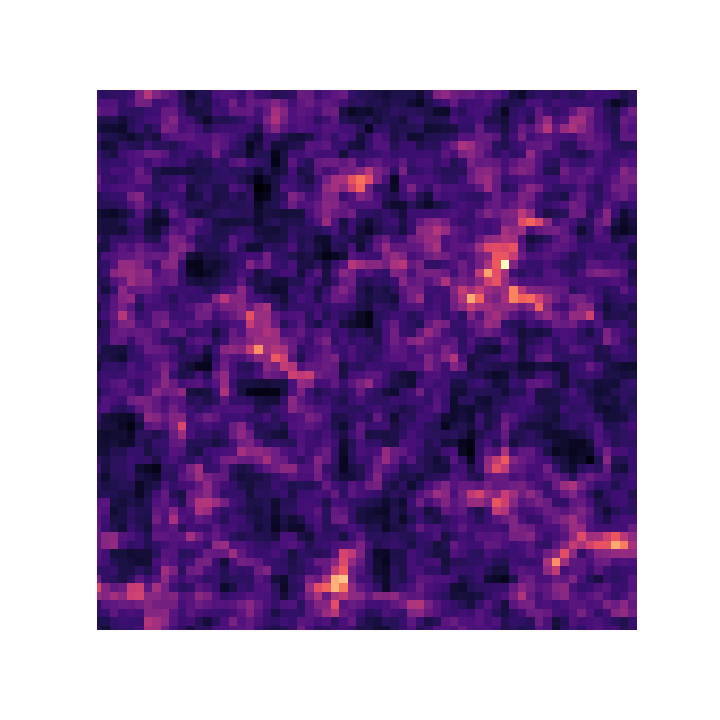


$\Longrightarrow$ Only a series of FFTs and interpolations.
introducing FlowPM: Particle-Mesh Simulations in TensorFlow


import tensorflow as tf
import flowpm
# Defines integration steps
stages = np.linspace(0.1, 1.0, 10, endpoint=True)
initial_conds = flowpm.linear_field(32, # size of the cube
100, # Physical size
ipklin, # Initial powerspectrum
batch_size=16)
# Sample particles and displace them by LPT
state = flowpm.lpt_init(initial_conds, a0=0.1)
# Evolve particles down to z=0
final_state = flowpm.nbody(state, stages, 32)
# Retrieve final density field
final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions),
final_state[0])
- Readily automatically differentiable
- Seamless interfacing with deep learning components
Mesh FlowPM: distributed, GPU-accelerated, and automatically differentiable simulations

- We developed a Mesh TensorFlow implementation that can scale on GPU clusters (horovod+NCCL).
- For a $2048^3$ simulation:
- Distributed on 256 NVIDIA V100 GPUs
- Runtime: 3 mins
- Don't hesitate to reach out if you have a use case for model parallelism!
![]()
Hybrid Physical-Neural ODE (WIP)
- Neural network parametrising a correction to the gravitational potential as a Fourier-based isotropic filter.
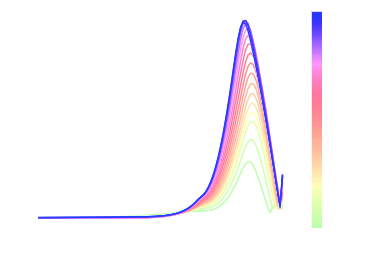
def neural_nbody_ode(a, state):
pos = state[0]; vel = state[1]
#### Compute gravitational forces
delta = flowpm.cic_paint(tf.zeros([batch_size, nc, nc, nc]), pos)
delta_k = r2c3d(delta)
pot_k = delta_k * laplace_kernel(kvec) * longrange_kernel(kvec)
# Neural potential correction
pot_k = pot_k * (1 + apply_model(kvec, a))
######################################
forces = tf.stack([ flowpm.cic_readout(
c2r3d(pot_k *gradient_kernel(kvec, i)), pos)
for i in range(3) ], axis=-1)
forces = forces * 1.5 * cosmo.Omega_m
#######################################
#Computes the update of position (drift)
dpos = 1. / (a**3 * flowpm.tfbackground.E(cosmo, a)) * vel
#Computes the update of velocity (kick)
dvel = 1. / (a**2 * flowpm.tfbackground.E(cosmo, a)) * forces
return tf.stack([dpos, dvel], axis=0)
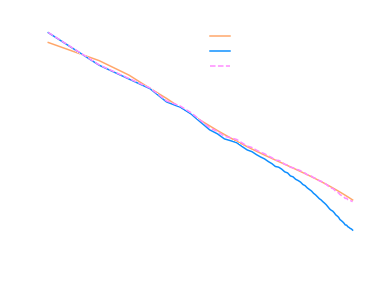
Different boxsize
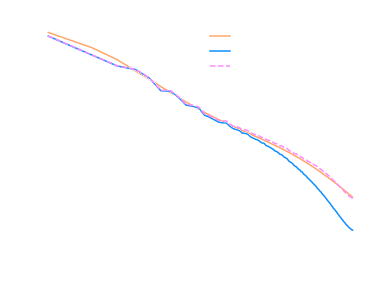
Different resolution
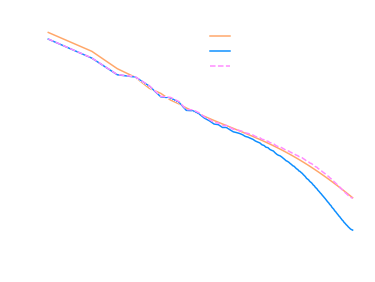
Different Cosmology!
Example use-case: reconstructing initial conditions by MAP optimization
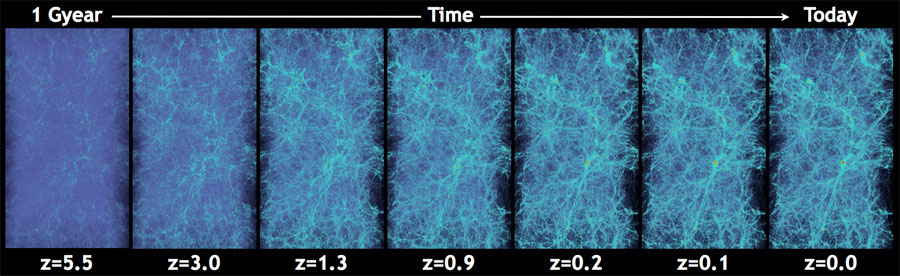
Going back to simpler times...
$$\arg\max_z \ \log p(x_{dm} = f(z)) \ + \ p(z) $$
where:
- $f$ is FlowPM
- $z$ are the initial conditions (early universe)
- $x_{dm}$ is the present day dark matter distribution
MAP optimization in action
$$\arg\max_z \ \log p(x_{dm} = f(z)) \ + \ p(z) $$credit: C. Modi
True initial conditions
$z_0$

Reconstructed initial conditions $z$

Reconstructed dark matter distribution $x = f(z)$

Data
$x_{DM} = f(z_0)$
Check out this blogpost for more details
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html
https://blog.tensorflow.org/2020/03/simulating-universe-in-tensorflow.html
A closer look at the optimization algorithm
$$\arg\max_x \ \log p(y | f(x)) \ + \ p(x) $$
- Standard Gradient Descent Algorithm:
$$x_{i+1} = x_i - \epsilon \left[ \nabla_x{\log p(y | f(x_i))} + \nabla_x \log p(x_i) \right]$$
$$x_{i+1} = x_i - \Gamma \left(\nabla_x{\log p(y | f(x_i))}, \nabla_x \log p(x_i) \right]$$ with update function $\Gamma: (u,v) \rightarrow \epsilon(u + v)$ - Many algorithms (e.g. ADAM, LBFGS) can expressed in this form with a different choice of $\Gamma$.
$\Longrightarrow$ What if we could learn this update function?
Recurrent Inference Machines for Solving Inverse Problems
Putzky & Welling, 2017
- Introduce a Recurrent Neural Network (RNN) $h_\phi$, and state variable $s$, so that: $$ s_{i+1} = h^*_\phi( \nabla \log p(y|x_{i}), x_i, s_{i})$$ $$ x_{i+1} = x_i + h_\phi(\nabla \log p(y|x_{i}), x_i, s_{i+1})$$
- Train according to: $$\mathcal{L} = \sum_{i}^T w_i\mathcal{L}(x_i, x)$$
CosmicRIM: Recurrence Inference Machines for Initial Condition Reconstruction
Recurrent Neural Network Architecture
![]()
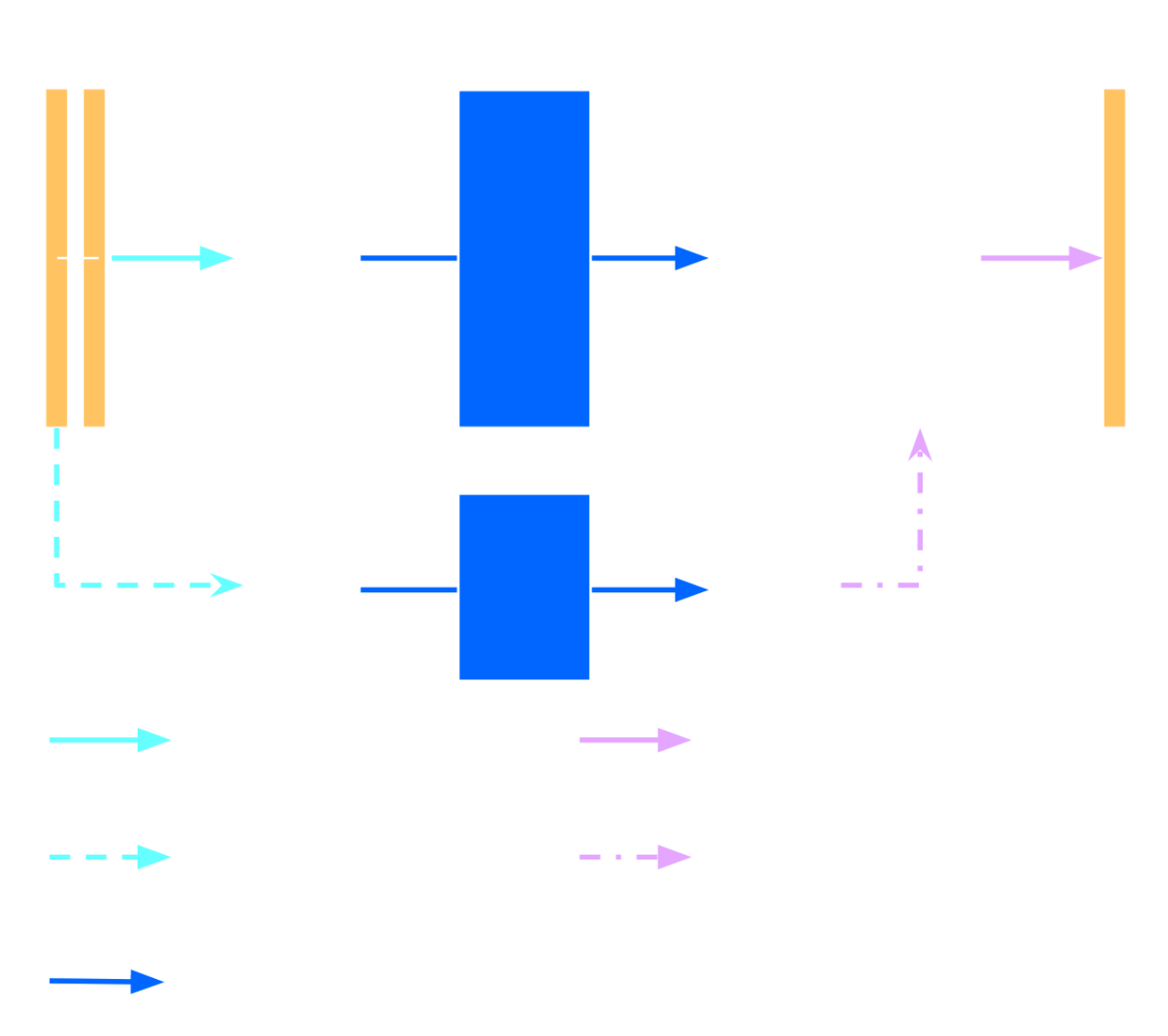
- A few notable differences to a vanilla RIM:
- We provide gradients of both prior and likelihood to the model.
- Because our forward model couples scales, we use a multiscale U-Net architecture.
- Input gradients are pre-scaled with the ADAM formula.
Experiments
Settings
- Forward model: $64^3$ particles, 400 Mpc/h box, 2LPT dynamics with 2nd order bias model
- RIM: 10 steps, trained under l2 loss
Initial conditions cross-correlation
![]()
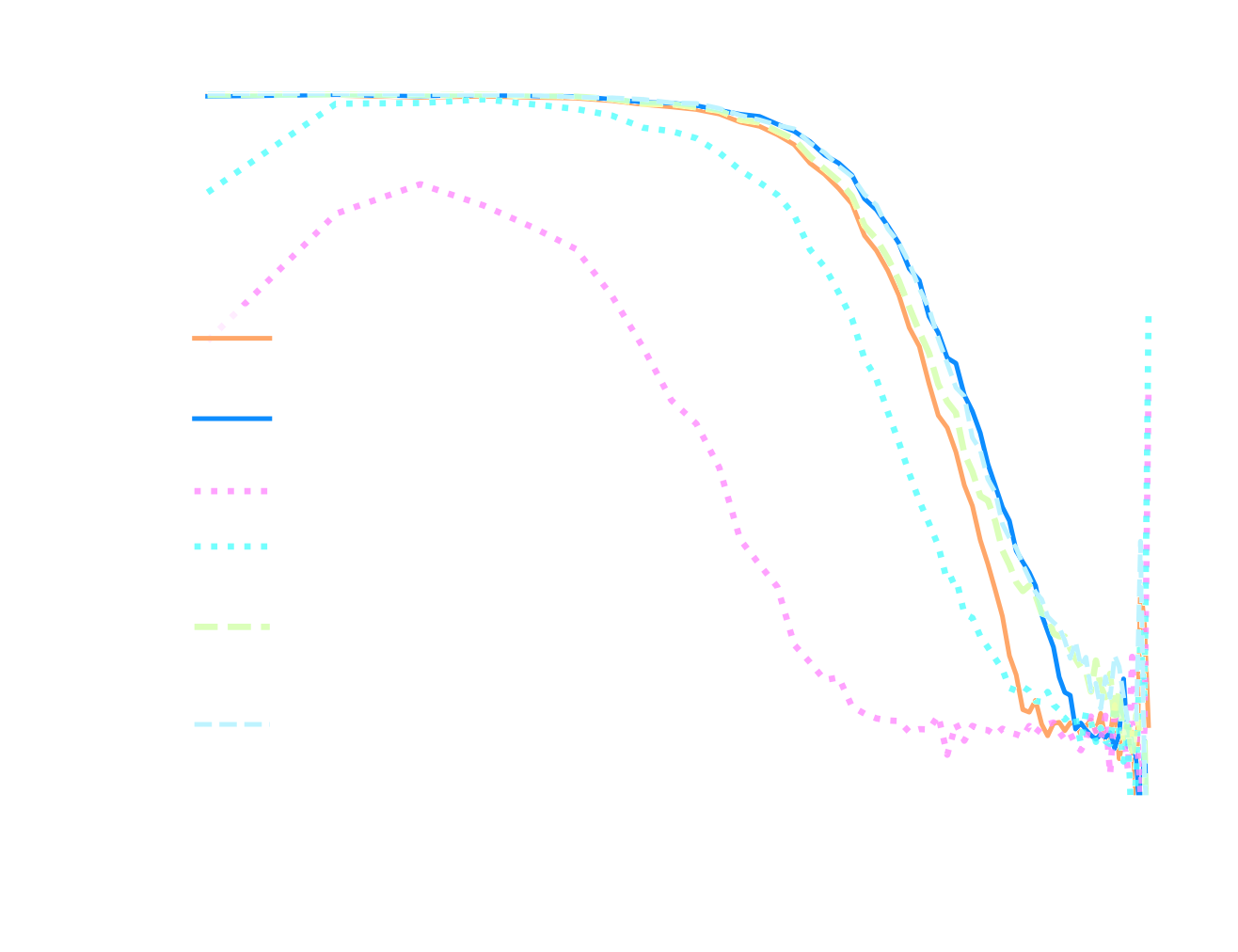
Transfer function
![]()
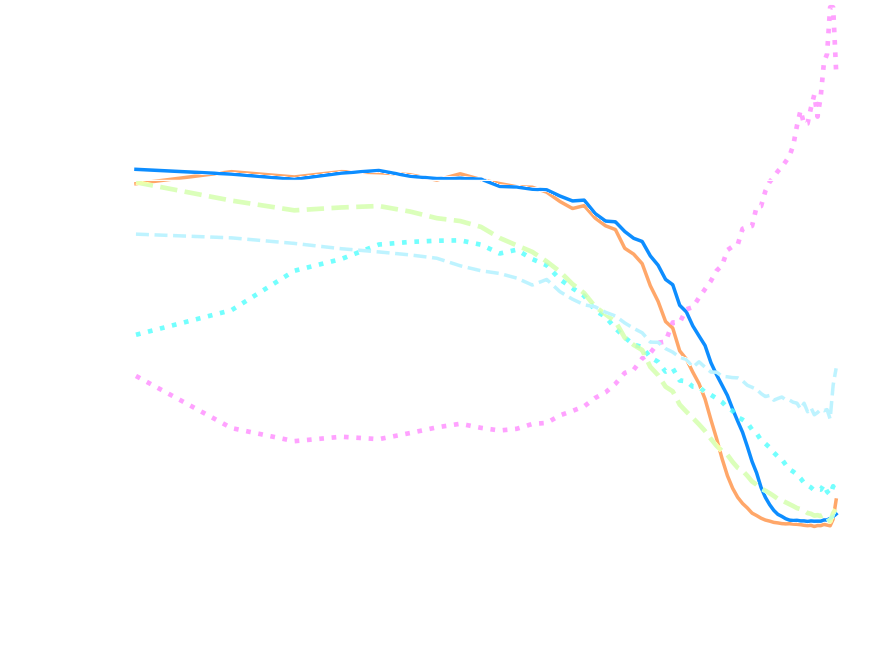
- CosmicRIM: Learn to optimize by embedding a Neural Network in the optimization algorithm.
$\Longrightarrow$ converges 40x faster than LBFGS.
Conclusion
Conclusion
Merging Deep Learning and Physical Models
- Complement known physical models with data-driven components
- Learn galaxy morphologies from noisy and PSF-convolved data, for simulation purposes.
- Use data-driven model as prior for solving inverse problems such as deblending or deconvolution.
- Leverage simulators as physical models for parameter inference
- Lifts the restrictions of analytic summary statistics (like 2pt functions)
- Provides full automated inference methodology that only requires a simulator
- Automatically differentiable physical models
- Allows for fast inference in high dimensions.
- Can be interfaced with neural networks in plenty of exciting ways.
Free advertisement:
- ICML 2022 Workshop on Machine Learning for Astrophysics, extended abstract submission deadline May 23rd.
$\Longrightarrow$ The theme is how to make machine learning useful for science.
Thank you !